Achronix立异的机器学习处理器(MLP)打破传统FPGA运算瓶颈
作者:杨宇,Achronix资深现场运用工程师
跟着机器学习(Machine Learning)范畴越来越多地运用现场可编程门阵列(FPGA)来进行推理(inference)加快,而传统FPGA只支撑定点运算的瓶颈越发凸显。 Achronix为了处理这一大窘境,立异地规划了机器学习处理器(MLP)单元,不只支撑浮点的乘加运算,还能够支撑对多种定浮点数格局进行拆分。
MLP全称Machine Learning Processing单元,是由一组至多32个乘法器的阵列,以及一个加法树、累加器、还有四舍五入rounding/饱满saturation/归一化normalize功能块。一起还包含2个缓存,分别是一个BRAM72k和LRAM2k,用于独立或结合乘法器运用。MLP支撑定点形式和浮点形式,对应下面图1和图2。
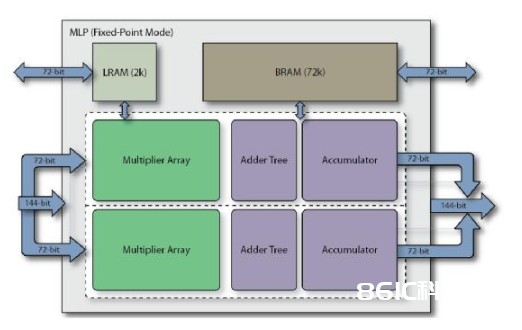
图1 定点形式下的MLP框图
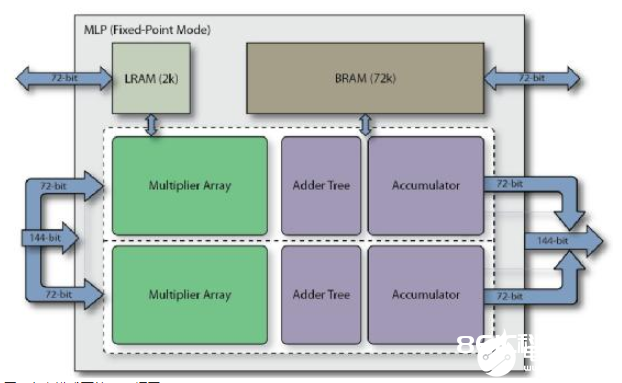
图2 浮点形式下的MLP框图
考虑到运算能耗和准确度的折衷,现在机器学习引擎中最常运用的运算格局是FP16和INT8,而Tensor Flow支撑的BF16则是经过下降精度,来取得更大数值空间。下面的表1是MLP支撑的最大位宽的浮点格局,表2说明晰各自的取值规模。

表1 MLP支撑的最大位宽的浮点格局
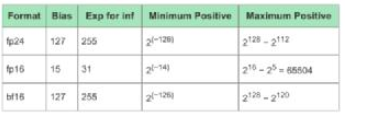
表2 不同运算格局的取值规模
而且这好像也成为未来的一种趋势。现在已经有不少研讨标明,更小位宽的浮点或整型能够在确保正确率的一起,还能够削减很多的核算量。因而,为了适应这一潮流,MLP还支撑将大位宽乘法单元拆分红多个小位宽乘法,包含整数和浮点数。详见下表3。
值得注意的是,这儿的bfloat16即Brain Float格局,而block float为块浮点算法,即当运用Block Float16及更低位宽块浮点格局时,指数位宽不变,小数位减缩到了16bit以内,因而浮点加法位宽变小,而且不需要运用浮点乘法单元,而是整数乘法和加法树即可,MLP的架构能够使这些格局下的算力倍增。
表3是Speedster7t系列1500器材所支撑的典型格局下的算力比照,能够看到,单片FPGA的浮点算力最高可到达123TOPS。
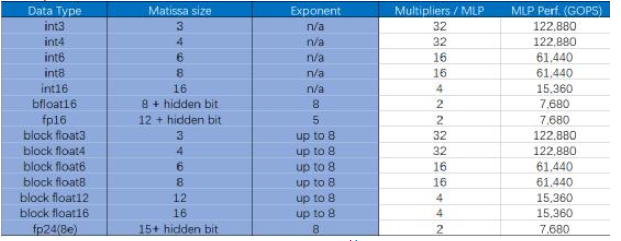
表3 Achronix的Speedster7t系列1500器材支撑的典型格局的算力比照
下图3是MLP中FP24/FP16乘加单元的简化结构图,即一个MLP支撑FP24/FP16的A*B+C*D,或许A*B,C*D。
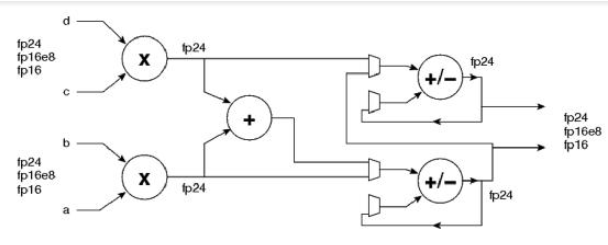
图3 MLP中FP24/FP16乘加单元的简化结构图
而以下的图4则是块浮点乘加单元结构。
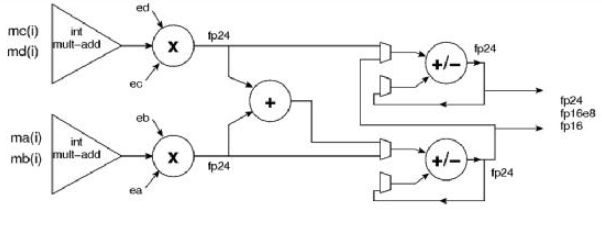
图 4 块浮点乘加单元结构
这儿考虑浮点数序列块ai=mai∙2ea,浮点数序列块bi=mbi∙2eb,各序列块内均具有相同的指数ea和eb。则
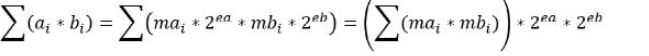
不难看出,乘法单元的个数取决于尾数(即整数)位宽。

表4 MLP中乘法单元的个数与整数位宽的联系