概要
东西
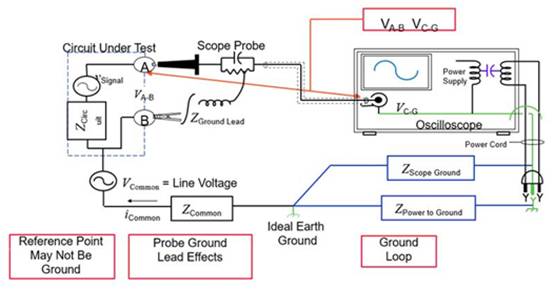
因为独自丈量无法供给之前或下一次丈量的任何信息,随机进程很难量化,只能检查该进程的累积丈量。Figure 1展现了用于比方噪声这样的随机进程的根本丈量东西,最上面的迹线是输入通道2的起伏时刻曲线。底下的迹线是显现噪声随频率散布的功率谱密度曲线。再下面的迹线是独自的噪声电压丈量的直方图,展现了独自丈量的幅值散布。最下面的迹线是通道每1000个收集点的规范方差趋势,显现出在屡次丈量中丈量值的改变。这些剖析功用,结合丈量参数,供给了噪声丈量的完好东西。
时域丈量
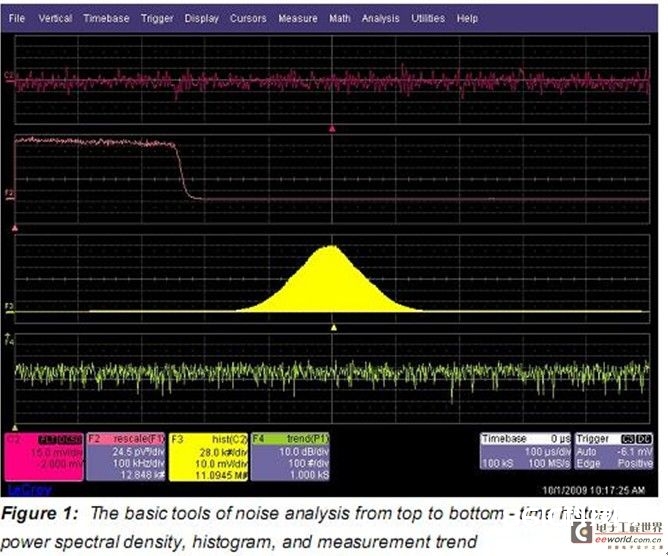
让咱们从大部分根本丈量开端。Figure 2中咱们做了带宽受限噪声波形的时域丈量。经过运用丈量参数取得了噪声信号特征的一些知道。大多数有意义的参数是波形的平均值,规范方差,峰峰值。这些丈量的规范方差,能够描绘为沟通有效值,被看作成波形的有效值对错常有用的。参数计算可显现平均值,最大值,最小值,规范方差,计算的丈量值数量。读出参数下的小直方图称为histicons,显现了相关参数丈量值的散布。
直方图
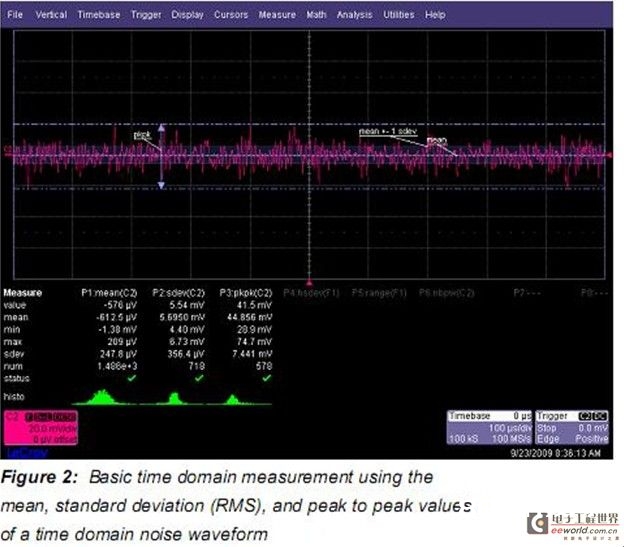
噪声呈高斯散布,平均值和规范方差用来描绘噪声的概率密度函数(pdf)。直方图供给了丈量参数散布的简略视图。Figure 3 显现了收集样本值的直方图。该直方图为用户供给了带有被测进程的概率密度函数的估量。这个数据能够运用直方图参数解说。Figure 3 显现了3个直方图参数,hmean,hsdev,和range,分别是平均值,规范方差,规模的直方图散布。直方图可由单次采样或屡次采样计算出来。这两种状况都能供给被研讨进程的很多实质知道。这个比如中的伪高斯散布标明信号源是一个随机进程。
Figure 4 的直方图稍有不同。散布的宽度增加了而且有2个峰。这是因为本来的随机噪声中存在小的正弦重量而引起的。正弦波散布有2个峰而且2个混合波形围绕着构成波形的散布。经过调查散布的形状能够了解被测进程发生了什么。在开端任何丈量之前调查噪声散布无疑是一个好的实践。