简介
在本系列的榜首篇文章中1,我调查了滤波器相位与滤波器完结拓扑结构的联系。 在第二篇文章中2,我调查了低通和高通呼应滤波器传递函数的相位偏移。 这篇文章将要点评论带通呼应。 尽管滤波器首要针对起伏呼应而规划,但在一些运用中,相位呼应或许非常重要。
出于调查意图,有源滤波器的传递函数实践上是滤波器传递函数和放大器传递函数的级联(见图1)。

带通传递函数
把低通原型的分子改为 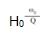 ,成果将把滤波器变成一个带通函数。 这会在传递函数内引进一个零点。 分子中的一个s得到一个零点,分母中的一个s得到极点。 零点将发生频率上升呼应,而极点将发生频率下降呼应。
,成果将把滤波器变成一个带通函数。 这会在传递函数内引进一个零点。 分子中的一个s得到一个零点,分母中的一个s得到极点。 零点将发生频率上升呼应,而极点将发生频率下降呼应。
二阶带通滤波器的传递函数变为:
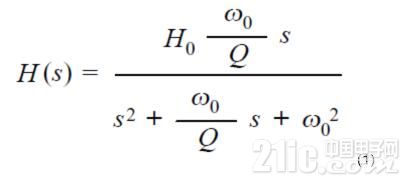 (1)
(1)此处的ω为滤波器增益峰值化时的频率(F0 = 2 π ω0)。
H0为电路增益(Q峰值化),界说为:

其间,H为滤波器完结的增益。
对带通呼应来说,Q有特别含义。 它是滤波器的挑选性。 界说为:
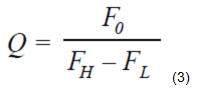
其间,FL和FH为呼应比最大值相差–3 dB时的频率。
滤波器的带宽(BW)界说为:
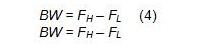
能够证明,谐振频率(F0)为FL和FH的几许平均值,这就意味着,F0在对数规范大将出现在FL和FH二者的中点。
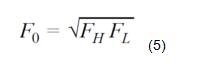
另需留意的是,在对数规范上,带通呼应的波裙在F0左右始终是对称的。
带通滤波器对各种Q值的起伏呼应如图2所示。在此图中,中心频率的增益归一化为1 (0 dB)。
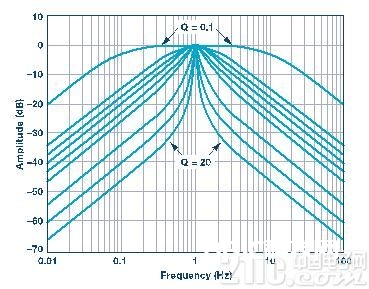
尽管本文首要重视相位呼应,但了解下滤波器起伏呼应也很有用。
这儿需求提示一下。 带通滤波器有两种界说方法。 窄带状况为经典界说,如上文所示。 可是,在某些状况下,假如高、低截止频率相差很大,则带通滤波器选用独立的高通和低通部分进行结构。 这儿所说的相差很大是说至少相差2个倍频程(频率×4)。 这便是宽带状况。 本文中,咱们首要重视窄带状况。 关于宽带状况,可将滤波器视为独立的高通和低通部分。
尽管带通滤波器可用巴特沃兹、贝塞尔或切比雪夫等规范呼应界说,但它们也一般依照其Q和F0界说。
带通滤波器的相位呼应为:

请留意,不存在单极点带通滤波器。
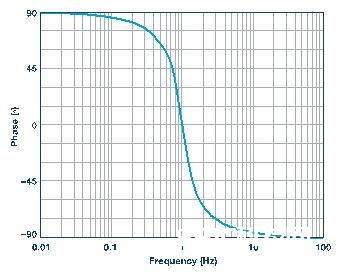
图3从中心频率的1%到中心频率的100倍对公式6进行估值。 中心频率的相移为0°。 中心频率为1,Q等于0.707。 此Q与前一篇文章中运用的Q相同,但该篇文章中咱们运用的是α。记住,α = 1/Q。
调查后发现,此曲线的形状基本上与低通(和相应的高通)的曲线形状相同。 可是,本例中相移从中心频率下方90°开端,在中心频率处趋于0°,最终完毕于中心频率上方–90°。
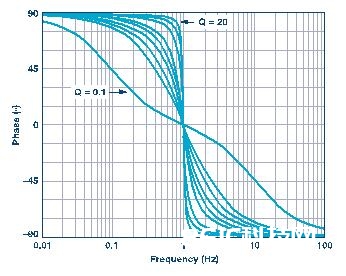
在图4中,咱们调查了在Q不断改变时带通滤波器的相位呼应。调查传递函数能够发现,相位改变或许发生在相对较大的频率规模内,改变的规模与电路的Q成反比。 相同,在调查后发现,曲线的形状与低通(和高通)呼应相同,仅规模有差异。
放大器传递函数
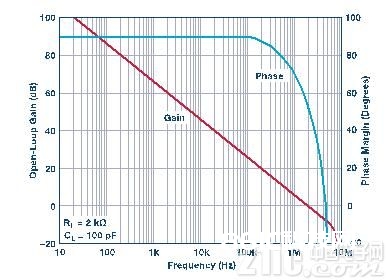
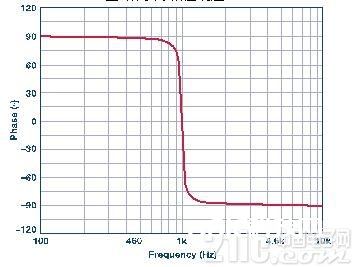
之前的部分显现,传递函数基本上便是单极点滤波器的传递函数。 尽管放大器的相移一般被忽视,但它可影响复合滤波器的全体传递。 本文随机挑选了AD822用于滤波器的仿真。 这样挑选的部分原因是为了最大程度地下降对滤波器传递函数的影响。 这是因为,放大器相移的频率显着高于滤波器自身的转机频率。 AD822的传递函数如图5所示,其信息直接取自数据手册。
示例1: Q = 20的1 kHz 2极点带通滤波器
榜首个示例开端时是作为带通规划的滤波器。 咱们随意挑选了一个1 kHz的中心频率和数值为20的Q。因为Q在较高的一侧,因而咱们将运用双放大器带通(DABP)装备。 相同,这是随意挑选的。
咱们运用参阅1的规划公式。相应的电路如图6所示:

本文中咱们首要重视相位,但我以为调查下起伏呼应也很有用。
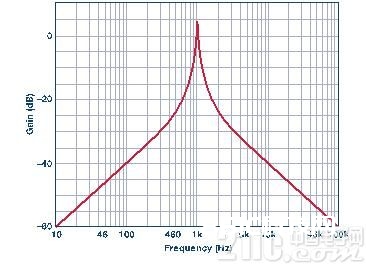
图8所示为相位呼应:
应当留意,DABP装备为同相。 图8与图3共同。
示例2: 从1 kHz、3极点0.5 dB切比雪夫低通到带通滤波器的转化
滤波器原理以低通原型为根底,低通原型能够其他方式表明。 本例运用的原型是1 kHz、3极点、0.5 dB切比雪夫滤波器。 挑选切比雪夫滤波器是因为,假如呼应不正确,它能够显现得更清楚。 例如,通带中的纹波将不会排成一行。 在本例中,巴特沃兹滤波器或许过于宽松。 挑选3极点滤波器是为了能够转化一个极点对和单个极点。
LP原型的极点方位(来自参阅1)为:

榜首级为极点对,第二级为单极点。 请留意,用α表明两个彻底不同的参数的做法是不可取的。 左边的α和β为复平面上的极点方位。 这些是转化算法中运用的值。 右侧的α为1/Q,这正是物理滤波器规划等式所期望看到的。
现在,低通原型被转化成了带通滤波器。 参阅1中列出的一系列等式用于转化。 原型滤波器的每个极点都将转化成一个极点对。 因而,转化完结时,3极点原型将具有6个极点(3个极点对)。 此外,原点处将有6个零点。 不存在单极点带通。
转化进程的部分作业是指定可组成的滤波器的3 dB带宽。 在这种状况下,该带宽将被设为500 Hz。 发生的转化成果如下:
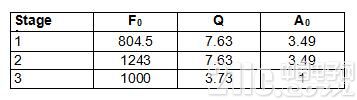
实践上,先将更低的增益和Q部分放入串中或许很有用,因为这可最大程度地进步信号电平处理才能。 前两级存在增益要求的原因在于,相关于总滤波器中心频率,它们的中心频率将会衰减(也便是说,它们将在其他部分的波裙上)。
因为成果得到的Q适中(小于20),因而将选用多级反应拓扑结构。 咱们运用参阅1中多路反应带通滤波器的规划方程规划滤波器。 图9显现了滤波器自身的原理图。
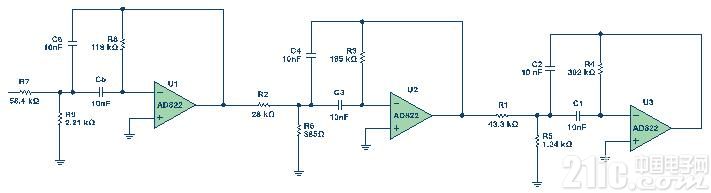
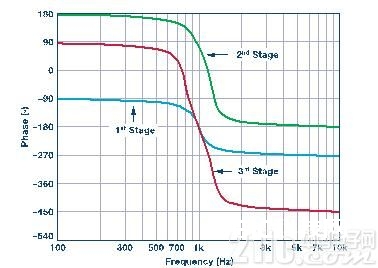
图10. 1 kHz、6极点、0.5 dB切比雪夫带通滤波器的相位呼应
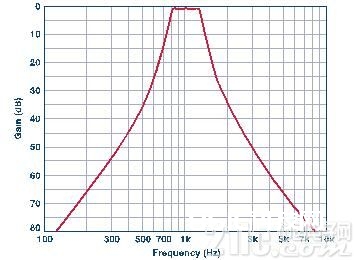
图10中能够看到完好滤波器的相移。 曲线图独自显现了榜首部分的相移(第1部分)、前两个部分的组合相移(第2部分),以及完好滤波器的相移(第3部分)。 这些曲线显现了“实践”滤波器部分的相移,其间包含放大器的相移和滤波器拓扑结构的反相。
图10中有几点细节需求留意。榜首,相位呼应具有累积性。 榜首部分显现了180°的相位改变(滤波函数的相移,忽视了滤波器拓扑结构的相移)。 第二部分显现了因具有两部分而发生的360°相位改变,每个部分180°。 记住,360° = 0°。 第三部分显现了540°的相移,每个部分180°。 还应留意,在高于10 kHz的频率处,咱们开端看到相位因放大器呼应而细微滚降。 还能够看出,滚降也具有累积性,会跟着每个部分而增大。
在图11中咱们能够看到完好滤波器的起伏呼应。
定论
本文评论的是带通滤波器的相移。 在前面几篇文章中,咱们调查了与滤波器拓扑结构相关的相移以及低通和高通拓扑结构的相移。 在后续文章中,咱们将调查陷波滤波器和全通滤波器。 在最终一期,咱们将总结并调查相移怎么影响滤波器的瞬态呼应,一起还会调查群推迟、脉冲呼应、阶跃呼应,以及它们对信号的含义。