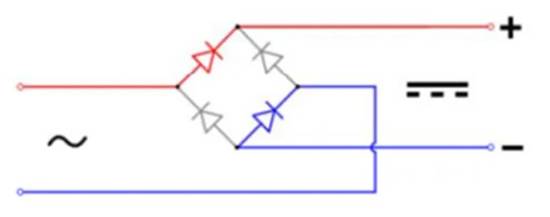
最近一时冲动,买了一个本钱十分低的电子骰子套件。拼装的进程仍是挺有古典兴趣的。这个电路的规划风格还停留在70年代:一个CD4017,一个NE555,一对晶体管。当然,我开端考虑,怎样用最高效的方法来完成呢?当然这意味着需求用到微操控器;并且还要到达咱们资源运用尽或许低的方针。那么用一个带有3个I/O口的ATtiny10能够完成吗?
骰子的图画包括7个LED,可是,你或许很快就发现其间六个LED都是成对亮灭的,所以咱们就具有3对LED外加一个额定的LED需求操控。这需求四个I/O口——但仍是太多了!
要削减需求的I/O口,一个很显然的运用方法是“查理复用技能(Charliplexing)”,你能在网上找到许多关于查理复用技能电子骰子的电路图。简略来说,查理复用技能答应运用n个I/O口操控n²-n个LED。所以当咱们选用查理复用技能时,咱们就需求三个I/O口就够了。但对于咱们运用的ATtiny10来说仍是太多了,由于咱们还需求一个额定的I/O口来“摇骰子”。
查理复用技能运用了微操控器I/O引脚的三态特性。一起激活的只要两个I/O口——其间一个为高电平,另一个为低电平——而其他引脚便是高阻抗状况。只要以正确的极性和激活的引脚直接相连的LED才干发光。而不与引脚直接相连的途径上的LED——比方衔接到激活引脚的的是两个串联的LED——那么这些LED就不会发光,这是由于二极管的非线性电流-电压特性导致的。
现在,你或许会疑问当只要一个I/O口(而不是两个)激活时会产生什么了?在查理复用技能的计划中什么也不会产生,但咱们能够运用这一点。
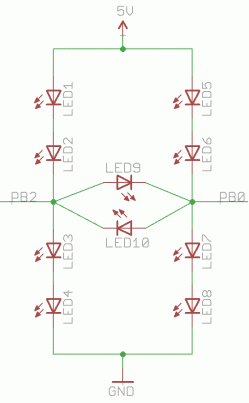
以上的电路展现了怎样以不同的计划衔接LED。除了两个I/O引脚之间的反平行对之外,作为查理复用技能的运用习气,LED还需求衔接到VCC(5V)和GND。串联的四个LED(LED1-4与LED5-8)的正向电压之和超越5V,所以当PB0和PB2处于高阻抗(Z)状况时,这些灯都不会发光。
当PB0和PB2中有一个引脚处于高电平或低电平状况,而另一个引脚为高阻抗状况时,那就会有一对LED会发光。而当PB0为高电平而PB2为低电平或恰好相反时,LED9或LED10就将和一对LED并联。这时大部分的电流会流过单个LED,所以这时只要LED9或LED10会发光。
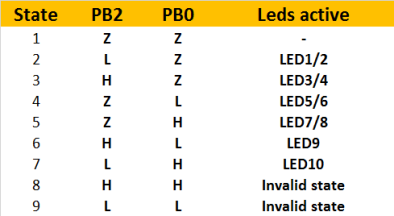
上表是或许的编码。看到了吗?两个引脚能够操控六个部分的LED!这正是咱们所需求的,使命完成了。
但需求阐明一点:单个LED的亮度并不同于串联的两个LED。这或许需求在查理复用技能中进行校对。可是事实上由于人眼对光亮度的差异并没有特别灵敏,两者的差异只能说是牵强可见。
简略测验一下(LED并未像骰子相同摆放)。看起来咱们新的多复用技能能很好地作业。留意一点,该电路需求由AVR I/O接口的内部阻抗。这的确有用,可是在“真实”的规划中应当防止。


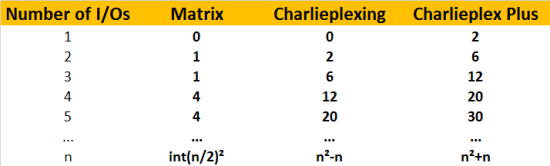
咱们能够讲这种新的计划成为“查理复用+(Charlieplex Plus)”。剖析标明,依托这样的技能,一个I/O口能够比一般的查理复用技能多操控两个LED。也便是说n个I/O口所能操控的LED数量就为2n+n²-n = n²+n。具体情况如上表所示。
你应该在你的规划中选用这种思路吗?恐怕不应该,由于这种做法的缺点和约束乃至比现有的查理复用还多。可是这却很风趣!
所以回到开始,操控电子骰子最少需求多少个I/O口呢?
答案是2.