呼吸和心跳是保持人体正常推陈出新和功用活动所有必要的生理进程。在生命勘探和医学研讨范畴,都需求进行心跳呼模型的仿真。MATLAB是MathWorks公司于1982年推出的一款高性能的数值核算和可视化数学软件。它能够用来求解各类学科问题,包含信号处理、图象处理、神经网络、控制系统辨识等。用MATLAB对心跳呼吸进行仿真,能够大大提高仿真工作效率。
1 生命信号特征剖析
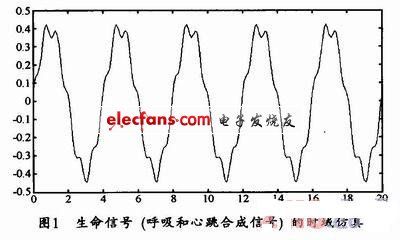
生命信号的规则性首要体现在心跳和呼吸的速率都很低。一般情况下,心跳次数约为每分钟70到80次,即使是剧烈运动时,也不过130次左右;而呼吸引起的胸腔崎岖一般约为每分钟20到30次,呼吸短促时也不过是60次左右,所以,人体生命信号的勘探,实践上便是低速运动方针的检测。在人体心情平稳时,心跳和呼吸的频率根本保持在一个安稳的范围内且呈周期性改变。
关于生命信号,许多情况下,也会出现出非规则性。一般情况下,为了简化剖析,能够将人体方针信号假设成具有周期性频率的正弦振荡信号。而实践上,人体呼吸引起的胸腔运动以及心跳都不是正弦曲线。并且,因为人与人之间的差异,不同人的生命信号起伏和频率等参数也是不同的。即使是同一个人,有些参数在不同的情况下也会发生改变。例如,人在受惊吓时,呼吸就会加速,然后导致呼吸信号的起伏
和频率升高。
2 跳呼吸模型仿真
2.1 正弦振荡模型
一般情况下,在生命勘探范畴,心跳和呼吸模型能够用两个正弦振荡函数来表明:
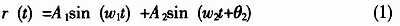
其间,A1和A2分别为呼吸和心跳的振幅;w1和w2分别为呼吸和心跳的频率;θ2是常数相位。
若将呼吸、心跳的频率和起伏参数设置为:A1=0.4cm,A2=0.05cm,w1=1.57rad,w2=9.42rad,θ2=0.956。那么,由以上设定参数并经过matlab软件所得出的心跳呼吸时域模型如图1所示。
2.2 用最小二乘法对实测波型进行曲线拟合
虽然人体的生命信号存在多样性和差异性,但是,人体的生理特点决议了人体的呼吸、心跳活动具有必定的规则性。有时候,人们需求的心跳呼吸信号相对较为杂乱,这时,就可依据实测波型进行模仿仿真。图2所示是在自由空间内,用34GHz线性接连波生物雷达进行勘探所得到的人体呼吸和心跳信号。
由图2能够看出,接连波雷达监测到的人体心跳和呼吸波形在单个周期内均有两个极大值和一个极小值。以心跳信号为例,在单个周期内,信号改变缓慢,波型上的拐点对应于人体心跳进程,能够用来作为标识心跳信号的特征点。其间,两个极大值是因为心房、心室出现周期性缩短、舒张所引起的。

依据接连波雷达监测到的人体呼吸的实测波形(即图2(a)),在单个周期波形上选取能反映波形改变的特征点如下:
x1=[0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5 2.75 3 3.1];
y1=[-0.24 -0.23 -0.1 1 -0.01 0.03 0.015 0.1 0.2 0.29 0.315 0.24 0.1 -0.2 -0.26];
再用最小二乘法曲线拟合,并使用matlab软件所得到的单周期人体规范呼吸波形如图3(a)所示,图中将其特征点用圆圈标出。

同理,依据图2(b)也可取如下特征点:
x1=[0 0.04 0.08 0.12 0.16 0.2 0.24 0.28 0.32 0.36 0.4 0.44 0.48 0.52 0.56 0.6 0.61];
y1=[-0.028 -0.02 0.01 0.039 0.049 0.05 0.048 0.04 0.034 0.028 0.026 0.029 0.034 0.037 0.032 0.004 0];
一起也用最小二乘曲线拟合,所得到的单周期人体规范心跳波形如图3(b)所示。
某些特别实验或许不方便或不能用前两种方法来对心跳、呼吸模型进行仿真,这时能够选用分段函数拟合法来树立模型。心脏缩短、舒张一次需求的时刻称之为心动周期,正常的成年人的心动周期约为0.72秒。取振幅为0.04cm,周期为0.72s,可将心脏的缩短、舒张简化为正弦分段函数:
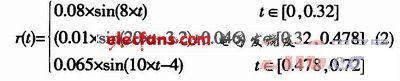
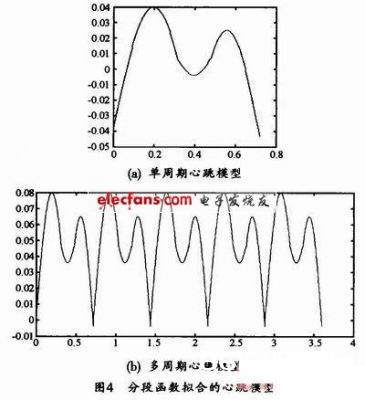
由式(2)得到的时域上的单周期和多周期心跳模型如图4所示。
3 结束语
本文对人体的心跳、呼吸特征及规则进行了剖析与研讨,并针对不同需求给出了根据matlab软件仿真的三种心跳、呼吸模型,包含正弦振荡模型、最小二乘法对实测波型进行曲线拟合模型、及分段函数拟合模型。仿真成果证明,三种模型均契合理论剖析及实践丈量。本文对生命勘探雷达、医学、生理学等许多科学的研讨和详细工程使用均有必定的参考价值。
.