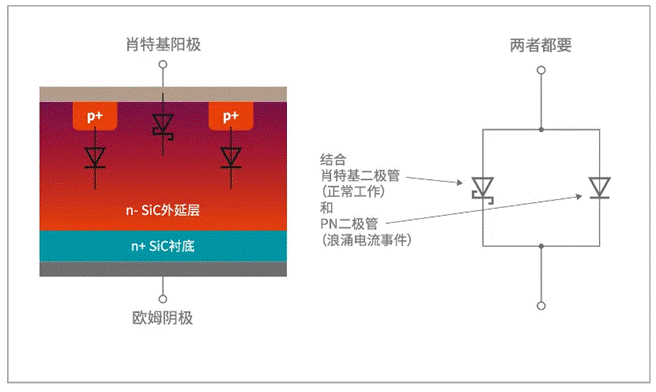
关于正弦信号,流过一个元器件的电流和其两头的电压,它们的相位纷歧定是相同的。这种相位差是怎么发生的呢?这种常识非常重要,因为不只放大器、自激振荡器的反应信号要考虑相位,并且在结构一个电路时也需求充沛了解、使用或防止这种相位差。下面讨论这个问题。
首要,要了解一下一些元件是怎么构建出来的;其次,要了解电路元器件的根本作业原理;第三,据此找到了解相位差发生的原因;第四,使用元件的相位差特性结构一些根本电路。
一、电阻、电感、电容的诞生进程
科学家经过长时间的调查、实验,弄清楚了一些道理,也经常出现了一些意料之外的偶尔发现,如伦琴发现X射线、居里夫人发现镭的辐射现象,这些偶尔的发现竟然成了巨大的科学成果。电子学范畴也是如此。
科学家让电流流过导线的时分,偶尔发现了导线发热、电磁感应现象,然后发明晰电阻、电感。科学家还从冲突起电现象得到创意,发明晰电容。发现整流现象而创造出二极管也是偶尔。
二、元器件的根本作业原理
电阻——电能→热能
电感——电能→磁场能,磁场能→电能
电容——电势能→电场能,电场能→电流
由此可见,电阻、电感、电容便是动力转化的元件。电阻、电感完成不同品种能量间的转化,电容则完成电势能与电场能的转化。
1 电阻
电阻的原理是:电势能→电流→热能。
电源正负两头储藏有电势能(正负电荷),当电势加在电阻两头,电荷在电势差效果下活动——构成了电流,其活动速度远比无电势差时的乱序自在运动快,在电阻或导体内磕碰发生的热量也就更多。
正电荷从电势高的一端进入电阻,负电荷从电势低的一端进入电阻,二者在电阻内部进行中和效果。中和效果使得正电荷数量在电阻内部出现从高电势端到低电势端的梯度散布,负电荷数量在电阻内部出现从低电势端到高电势端的梯度散布,然后在电阻两头发生了电势差,这便是电阻的电压降。相同电流下,电阻对中和效果的阻力越大,其两头电压降也越大。
因而,用R=V/I来衡量线性电阻(电压降与经过的电流成正比)的阻力巨细。
对沟通信号则表达为R=v(t)/i(t)。
留意,也有非线性电阻的概念,其非线性有电压影响型、电流影响型等。
2 电感
电感的原理:电感——电势能→电流→磁场能,磁场能→电势能(若有负载,则→电流)。
当电源电势加在电感线圈两头,电荷在电势差效果下活动——构成了电流,电流改动磁场,这称为“充磁”进程。若被充磁电感线圈两头的电源电势差吊销,且电感线圈外接有负载,则磁场能在衰减的进程中转化为电能(如负载为电容,则为电场能;若负载为电阻,则为电流),这称为“去磁”进程。
衡量电感线圈充磁多少的单位是磁链——Ψ。电流越大,电感线圈被冲磁链就越多,即磁链与电流成正比,即Ψ=L*I。对一个指定电感线圈,L是常量。
因而,用L=Ψ/I表达电感线圈的电磁转化才能,称L为电感量。
电感量的微分表达式为:L=dΨ(t)/di(t)。
依据电磁感应原理,磁链改动发生感应电压,磁链改动越大则感应电压越高,即v(t)=d dΨ(t)/dt。
归纳上面两公式得到:v(t)=L*di(t)/dt,即电感的感应电压与电流的改动率(对时间的导数)成正比,电流改动越快则感应电压越高。
3 电容
电容的原理:电势能→电流→电场能,电场能→电流。
当电源电势加在电容的两个金属极板上,正负电荷在电势差效果下分别向电容两个极板集合而构成电场,这称为“充电”进程。若被充电电容两头的电源电势差吊销,且电容外接有负载,则电容两头的电荷在其电势差下向外流走,这称为“放电”进程。电荷在向电容集合和从电容两个极板向外流走的进程中,电荷的活动就构成了电流。
要特别留意,电容上的电流并不是电荷真的流过电容两个极板间的绝缘介质,而仅仅充电进程中电荷从外部向电容两个极板集合构成的活动,以及放电进程中电荷从电容两个极板向外流走而构成的活动。也便是说,电容的电流其实是外部电流,而非内部电流,这与电阻、电感都纷歧样。
衡量电容充电多少的单位是电荷数——Q。电容极板间电势差越大,阐明电容极板被冲电荷越多,即电荷数与电势差(电压)成正比,即Q=C*V。对指定电容,C是常量。
因而,用C=Q/V表达电容极板储存电荷的才能,称C为电容量。
电容量的微分表达式为:C=dQ(t)/dv(t)。
因为电流等于单位时间内电荷数的改动量,即i(t)=dQ(t)/dt,
归纳上面两个公式得到:i(t)=C*dv(t)/dt,即电容电流与其上电压的改动率(对时间的导数)成正比,电压改动越快则电流越大。
小结:
v(t)=L*di(t)/dt标明电流改动构成了电感的感应电压(电流不变则没有感应电压构成)。
i(t)=C*dv(t)/dt标明电压改动构成了电容的外部电流(实践是电荷量改动。电压不变则没有电容的外部电流构成)。
三、元件对信号相位的改动
首要要提示,相位的概念是针对正弦信号而言的,直流信号、非周期改动信号等都没有相位的概念。
1 电阻上的电压电流同相位
因为电阻上电压v(t)=R*i(t),若i(t)=sin(ωt+θ),则v(t)=R* sin(ωt+θ)。
所以,电阻上电压与电流同相位。
2 电感上的电流落后电压90°相位
因为电感上感应电压v(t)=L*di(t)/dt,若i(t)=sin(ωt+θ),则v(t)=L*cos(ωt+θ)。
所以,电感上电流落后感应电压90°相位,或者说感应电压超前电流90°相位。
直观了解:想象一个电感与电阻串联充磁。从充磁进程看,充磁电流的改动引起磁链的改动,而磁链的改动又发生感应电动势和感应电流。依据楞次定律,感应电流方向与充磁电流相反,延缓了充磁电流的改动,使得充磁电流相位落后于感应电压。
3 电容上的电流超前电压90°相位
因为电容上电流i(t)=C*dv(t)/dt,若v(t)=sin(ωt+θ),则i(t)=L*cos(ωt+θ)。
所以,电容上电流超前电压90°相位,或者说电压落后电流90°相位。
直观了解:想象一个电容与电阻串联充电。从充电进程看,总是先有活动电荷(即电流)的堆集才有电容上的电压改动,即电流总是超前于电压,或者说电压总是落后与电流。下面的积分方程能表现这种直观性:
v(t)=(1/C)*∫i(t)*dt=(1/C)*∫dQ(t),即电荷改动的堆集构成了电压,故dQ(t)相位超前v(t);而电荷堆集的进程便是电流同步改动的进程,即i(t)与dQ(t)同相。因而i(t)相位超前于v(t)。
四、元件相位差的使用——RC文氏桥、LC谐振进程的了解
不管RC文氏桥,仍是LC的串联谐振、并联谐振,都是由电容或/和电感容元件的电压、电流相位差引起的,就像机械共振的节拍相同。
当两个频率相同、相位相位的正弦波叠加时,叠加波的起伏到达最大值,这便是共振现象,在电路里称为谐振。
两个频率相同、相位相反的正弦波叠加,叠加波的起伏会降到最低,甚至为零。这便是减小或吸收振荡的原理,如降噪设备。
当一个体系中有多个频率信号混合时,如果有两个同频信号发生了共振,那么这个体系中其它振荡频率的能量就被这两个同频、同相的信号所吸收,然后起到了对其它频率的过滤效果。这便是电路中谐振过滤的原理。
谐振需求一起满意频率相同和相位相同两个条件。电路怎么经过起伏-频率特性挑选频率的办法曾经在RC文氏桥中讲过,LC串并联的思路与RC相同,这儿不再赘述。下面咱们来看看电路谐振中相位补偿的大略估量(更准确的相位偏移则要核算)
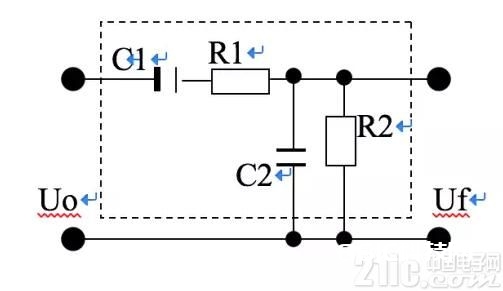
1 RC文氏桥的谐振(图1)
若没有C2,正弦信号Uo的电流由C1→R1→R2,经过R2上压降构成Uf输出电压。因为支路电流被电容C1移相超前Uo 90°,这超前相位的电流流过R2(电阻不发生相移!),使得输出电压Uf电压超前于Uo 90°。
在R2上并联C2,C2从R2获得电压,因为电容对电压的滞后效果,使得R2上电压也被强制滞后。(但纷歧定有90°,因为还有C1→R1→C2电流对C2上电压即Uf的影响,但在RC特征频率上,并联C2后Uf输出相位与Uo相同。)
小结:并联电容使得电压信号相位滞后,称为电压相位的并联补偿。
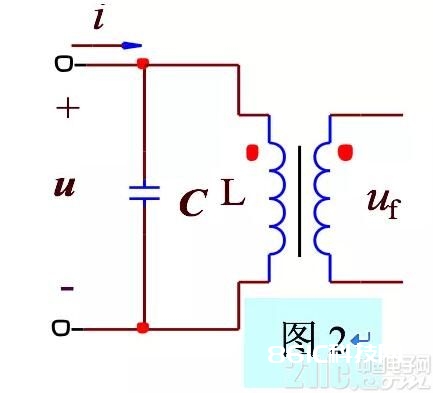
2 LC并联谐振(图2)
若没有电容C,正弦信号u经过L感应到次级输出Uf,Uf电压超前于u 90°;
在L初级并联电容C,因为电容对电压的滞后效果,使得L上电压也被强制滞后90°。因而,并联C后Uf输出相位与u相同。
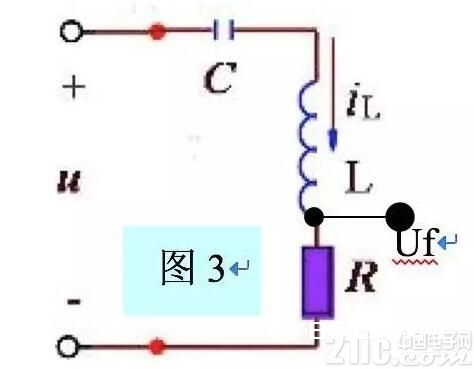
3 LC串联谐振(图3)
关于输入正弦信号u,电容C使得串联回路中负载R上的电流相位超前于u 90°,电感L则使得同一串联回路中的电流相位再滞后90°二者相位偏移刚好抵消。因而,输出Uf与输入u同相。
总结:(留意,相位影响纷歧定都是90°,与其它部分相关,详细则要核算)
串联电容使得串联支路电流相位超前,然后影响输出电压相位。
并联电容使得并联支路电压相位滞后,然后影响输出电压相位。
串联电感使得串联支路电流相位滞后,然后影响输出电压相位。
并联电感使得并联支路支路电压超前,然后影响输出电压相位。