公钥暗码体系,也称为非对称暗码体系,是暗码学的一种方法。它有一对密钥:公钥和私钥。它们在数学上有必定的联系,可是很难从公钥得到私钥。公钥暗码学的两个首要分支:
公钥加密:任何人都能够将音讯(明文)加密成密文,但只需接收者才干生成有意义的密文。这样确保了数据的安全性,用于可靠性方面。
数字签名:发送者经过私钥加密的音讯(明文),能够被任何人经过公钥解密。因而证明了这条音讯是发送者签名而且没被人修改正。这种办法用于数字签名与认证方面。
公钥制暗码学中,现在运用最为广泛的是RSA公钥制暗码算法[1]。RSA算法经过模幂运算完结,模幂运算是整个RSA算法的中心。在操作数较小的情况下,模幂运算比较简略,能够直接核算。可是为了确保必要的安全等级,一般选用512 bit或1 024 bit的密钥长度,在银行等需求更高安全等级的体系中,会选用更长位宽的密钥,模幂的难度随之成指数级添加。RSA算法安全性的确保和需求就像一把双刃剑,在给攻击者带来核算难度的一起也进步了运算的复杂度。
本文提出一种依据ASIC规划的高速、可装备的RSA暗码协处理器体系结构,可完结256 bit到2 048 bit的RSA加密运算。该计划归纳考虑RSA模幂和模乘算法的特色和瓶颈,选用改善的高基模乘算法和流水线结构,进步运算速度;选用DMA直接拜访方法,消除协处理器与内存之间的通讯速度瓶颈;数据输入输出都运用双口存储体,构成加解密数据流。
1 公钥暗码算法RSA
1.1 RSA算法
RSA加密算法是现在在理论和实践运用中较为成功的公钥暗码体系,它的安全性是依据数论中大整数分解为素数因子的困难性,这一困难在现在仍是一个NP问题。要树立一个RSA暗码体系,首要任选两个大素数p、q,使:
N=p×q
并得到Euler函数:
Ψ(n)=(p-1)×(q-1)
然后任选一个与Ψ(n)互素的整数e作为密钥,再依据e求出解密密钥d,d满意:
d×e=1modΨ(n)
事实上,加密密钥e宽和密密钥d是彻底可交换的,因而在求e或d时,不管先假定哪一个,再由它去求另一个都是相同的。对某个明文分组M和密文分组C,加密宽和密的进程如下:
加密进程:
C=MemodN
而解密进程是:
M=CdmodN
RSA加解密便是做模幂运算的进程,而模幂运算是经过一系列的模乘运算得到的。模幂算法依据幂指数扫描次序不同能够分为两种:从左往右的L-R算法和从右往左的R-L算法。
算法一:R-L模幂算法
式中n为指数e的位数,P为中心变量
输入:M,e,N;
输出:C=Me modN;
(1)P=M;C=1;
(2)for i=0 to n-2;
(3)if e[i]=1 then C=C×P mod N;
(4)P=P×P mod N;
(5)next i;
(6)if e[n-1]=1 then C=C×P mod N;
(7)return C;
算法二:L-R模幂算法
输入:M,e,N;
输出:C=Me modN;
(1)if e[n-1]=1 then C=M,else C=1;
(2)for i=n-2 to 1;
(3)C=C×C mod N;
(4)if e[i]=1 then C=C×M mod N;
(5)next i;
(6)return C;
从以上两种算法能够看出,一次模幂运算需求进行N次平方模运算和均匀N/2次乘法模运算;但在从右往左的扫描中,乘法和平方是彼此独立的,能够并行。因而能够添加一个N位的乘法器,一个做乘法,一个做平方,这能够明显进步一次模幂运算的速度。本文面向高速运用场合,因而选用R-L模幂算法。
在RSA算法中,不管是加密进程仍是解密进程,都有一个一起的模乘运算(ABmod N),这个看似简略的运算,需求做一次乘法和一次除法,终究取余数。但由于M,e,C,d,N等参数的长度一般是1 024个二进制位或更高,使得模幂运算量巨大,很难在一般的协处理器上或处理器上运转,直到1985年由Montgomery提出了一种免除法的模乘算法[2],才使RSA算法在硬件和软件中得以完结。
1.2 Montgomery模乘算法
Montgomery算法的基本思想是把一个大整数转化为一个模R(R一般取2r)的余数表明方法,用转化后的余数进行一系列模乘运算,终究再转化为正常的表达方法。将核算A*B mod N时的mod N的除法运算转化为简略的移位运算,能够有效地进步模乘运算的速度。
算法三:Montgomery算法
设N为模数,R是2的整数幂,且R>N,并令R-1和N′满意0-1-1-NN′=1建立。
输入:A,B,R,N;
输出:c=M(A,B)=A*B*R-1 modN
(1)T=A*B;
(2)m=(Tmod R)*N′ mod R;
(3)c=(T+mN)/R;
(4)if c>=N return c-N;
(5)else return m;
该算法不能直接完结RSA算法,需求进行相应的预处理才干消除R-1带来的影响(见算法五)。该算法依然包含大整数的乘法,因而需求对其进行改善,运用高基模乘算法(见算法四),细化为小整数的乘法,以便于硬件完结。别的,该算法终究需求判别m是否大于N,假如大于N,有必要再做减法,这在硬件规划上会添加额定的芯片面积。本文经过在模乘循环进程中添加一次循环,就能够免除终究的减法(见算法五)。
1.3 高基Montgomery算法
把n位大整数A,B,N别离表明成s位r进制整数,即A=(as-1 as-2…a0),B=(bs-1bs-2…b0)r,N=(ns-1ns-2…n0)r,且R=rs,s=n/r,则有N P>
算法四:高基Montgomery算法
Function M(A,B)
S:=0;m=0;
(1)核算中心成果m[i]:
for i=0 to s-1
{for j=0 to i
{s:=s+a[j]*b[i-j]+m[j]*n[i-j];}
m[i]:=s*n′[i] mod r;
s:=s+m[i]n[i]
s:=s/r;}
(2)核算终究成果并存于m[i]中:
for i=s to 2s-1
{for j=i-s+1 to s-1
{s=s+a[j]b[I-j]+m[j]n[I-j]}
m[i-s]:=s mod r
s:=s/r}
算法五:从右往左扫描的免减高基模乘算法
(1)预处理:
R2=R*R mod N;(事前核算出来,可消除R-1带来的影响)
P=M(M,R2);
C=1;
(2)中处理:
for i=0 to n-2
if e[i]=1 then C=M(C,P);
P=M(P,P);
next i;
if e[n-1]=1 then C=M(C,P);
return C;(核算C=M(Me))
(3)后处理:
C=M(C,1);(免除了montgomery算法每次的减法运算)。
2 协处理器体系结构
2.1 SPU全体结构与模块区分
SPU与CPU经过CROSSBAR[3]穿插通讯开关进行通讯,而SPU与MEM之间则采纳DMA方法直接通讯,这样能够消除数据存取的速度瓶颈。一起,当SPU进行加解密作业时,CPU能够并行履行其他指令(只需不发生数据相关)。
SPU区分为操控模块,数据通道和存储单元。其间操控单元首要用于密钥移位操控,操控密钥的降幂,并依据密钥发生乘或平方操控信号。别的,操控单元还包含一个状况操控器,用于对前处理、中处理和后处理各个运算环节的操控。
数据通道部分则由Montgomery模乘单元和平方单元构成,两个单元并行,依据操控单元发生的操控信号来进行相应的操作,发生部分积和中心成果。
存储单元巨细为8 Kbit,分为两部分。一部分是4 KB的RAM,用于加解密进程中暂存数据,以便构成流水线;另一部分是4 KB的ROM,用于寄存公钥和密钥,掉电能够保存数据。
体系框图如图1所示。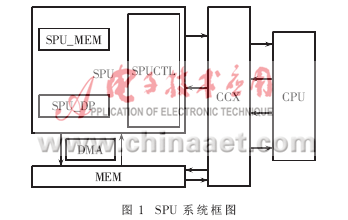
2.2 流水线规划
为了完结高速、可装备的RSA暗码协处理器,选用了按字读入的高基模乘算法,一起对模幂单元选用流水线结构:这样一方面能够添加数据吞吐率,加速数据运算速度;另一方面能够经过增减流水线的级数来增强可装备性。
从按字读入的高基模乘算法(算法五)中能够看出,每次密钥长度为N bit的RSA加解密进程是一次幂指数为N的模幂运算,而一次这样的模幂运算则是N次模乘运算。因而经过规划模幂流水线结构,能够大大添加RSA加解密的速度。
流水线结构的模幂运算如图2所示。明文M经过T级流水线数据通路,终究输出密文C;关于一个N位的RSA加密体系来说,假如选用T级流水线,则每一级流水线需求循环做N/T次MM运算。RSA的运算速度取决于一级流水线的速度。
2.3 DMA通道的作业进程
SPU向DMA操控器宣布DMA恳求,DMA操控器在接到SPU宣布的DMA恳求后,向CPU宣布总线恳求,恳求CPU脱离对总线的操控,而由DMA操控器接收对体系总线的操控;CPU在履行完当时指令的当时总线周期后,向DMA操控器宣布总线呼应信号,CPU脱离对体系总线的操控,处于等候状况(但一向监督DMAC);DMA操控器接收对体系总线的操控;DMA操控器向SPU宣布DMA应对信号,DMA操控器把存储器与SPU之间进行数据传送所需求的有关地址送到总线,经过操控总线向存储器和SPU宣布读或写信号,然后完结一个字节的传送;当设定的字节数据传送结束后(DMA操控器主动计数),DMA操控器将总线恳求信号变成无效,一起脱离对总线的操控;CPU检测到总线恳求信号变成无效后(CPU一向监督着),也将总线呼应信号变成无效,CPU康复对体系总线的操控,持续履行被DMA操控器中止的当时指令的当时总线周期。
2.4 存储体结构规划
SPU内部共规划两部分RAM,都运用双口存储体,首要用作数据输入、输出缓存。双口RAM分A和B两部分,每部分的深度32,宽度64,即32×64的存储空间;一块RAM能够存储2 KB的数据,输入输出各需求一块作为缓存,也便是说片内共规划4 KB的RAM。双口RAM的两部分是对称的,可是对每部分的读写都是独立的,当需求加密或解密时,数据先输入到A部分,当A部分输入满2 KB数据时,数据持续输入到B中,此刻运算模块读取A中的数据核算,当B部分数据输入满时,运算模块现已核算完A中的数据,然后读取B中的数据,输出则是相反的进程,如此构成加解密数据流,运算流程如图3所示。
本文依据改善的按字输入的从右往左扫描的高基Montgomery模乘算法,提出了一种高速、可装备的RSA加解密协处理器的AS%&&&&&%规划计划。该计划很好地处理了模幂和模乘运算的瓶颈问题,进步了算法并行性和运算功率。依据该计划能够方便地规划出各种速度和密钥长度的RSA暗码协处理器,特别对高速RSA商场具有很宽广的运用远景。