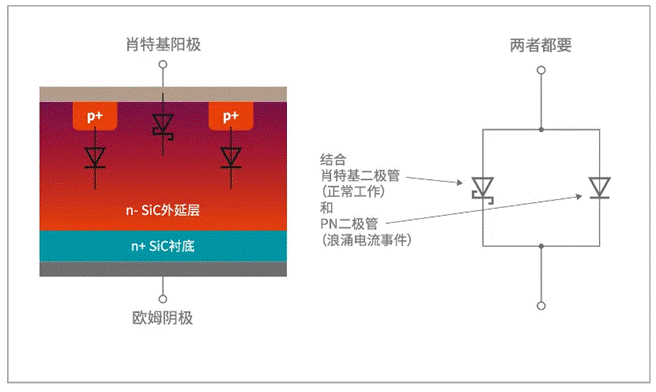
在最近一个项目中,我不得不翻开当年大学用的那本快速傅立叶改换(DFT)书本,书的封面上现已蒙上了厚厚的一层灰。实际上,我在作业过程中购买过不少DFT方面的书,虽然每本书都相对比较薄,但里边有许多公式和高阶数学运算,所以要“记住”比较突出的关键也算是一项应战。
谢天谢地,您现在即便不是DFT专家也能运用当时示波器中的FFT功用。可是,了解某些根底作业原理的确很有裨益。特别是,您挑选的窗口因子(window factor)或许会给丈量成果带来很大影响。
DFT剖析自身假定要处理的数据是单个周期的定时重复的信号。下面的图1介绍了一串时域样点。例如,在对图1中的第2个帧运用DFT处理时,将对信号进行周期扩展。后续帧之间的不接连点一般会如图2所示。这些假的不接连点会生成原始信号中没有的频谱假信号,从而不精确地重现信号。这种状况称为频谱走漏。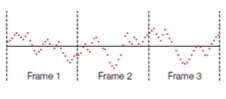
图1
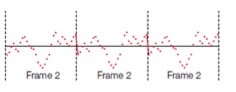
图2
示波器的FFT功用运用窗口技能,下降频谱走漏的影响。在履行DFT之前,DFT帧被乘以一个窗口函数,每个样点的长度相同。窗口函数一般呈钟形,会削减或消除DFT帧两头的不接连点。
图3显现了最常用的4个窗口函数,下面列明晰引荐用处:
1)矩形–丈量突发的瞬态信号,其间事情前的信号电平缓事情后的信号电平简直持平
2)Hamming –丈量正弦噪声、周期噪声或窄带随机噪声,其间事情前的信号电平缓事情后的信号电平显着不同
3)Hanning –在事情前和事情后的瞬态信号或突发信号电平显着不一起,丈量起伏精度(在解析频率处较低)
4)Blackman/Harris –丈量频率起伏,丈量以单频率为主的波形,查找高阶谐波
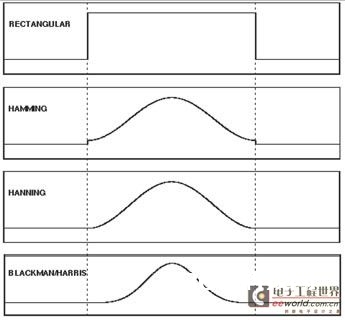
图3