摘要
高次谐波过流维护是一种特别的过流、过功率现象。一般用户的电路规划完全正确,惯例功率测验未超越额外功率。该种维护的定位及处理较为困难。本文结合理论剖析和实践经历剖析了高次谐波过流维护的原因,并供给了处理方案。
1、Class D 高次谐波过流维护现象
一般 Class D 功放芯片都会规划有过流维护功用,在输出电流超越限流阀值后芯片主动封闭驱动信号中止输出。一般的过流维护是由于输出功率超越额外或许输出短路而引起。还有一种特别的过流维护现象是由于高次谐波能量过大引起。高次谐波过流维护是一种特别的过功率现象。一般用户的电路规划完全正确,惯例功率测验未超越额外功率。这种维护具有以下几个特征:
l 问题机器在 1KHz 规范音频信号测验时输出功率并未超越最大输出功率。
l 播映高频成分较多的歌曲较简单呈现维护。
l 运用水泥电阻代替喇叭作为负载,维护现象消失。
l 减小,或许去掉输出 LC 滤波器的电容,维护现象消失。
若上述现象发生则能够怀疑是由于高次谐波能量引起的过流、过功率维护。高次谐波过流维护的原因较为杂乱,首要剖析一下 LC 滤波网络及喇叭阻抗的频率呼应特性。
2、LC 滤波器的频率呼应
图 1 是一个典型的 Class D 输出滤波网络(BTL 输出形式)。LC 滤波器由 L,C 和负载 R 组成。
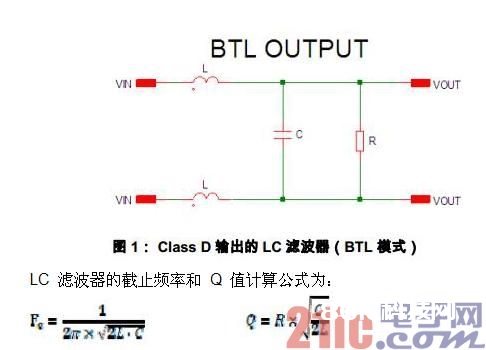
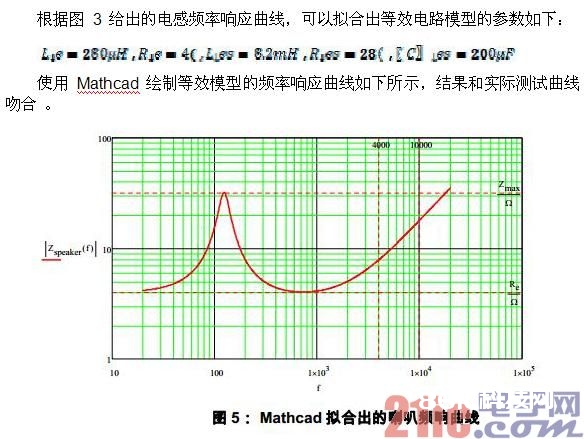
一般 Class D 的输出 LC 滤波器截止频率 设置在 30kHz — 50kHz 范围内,为的是供给足够大的高频衰减的一起不影响音频频带内的增益平整性。LC 滤波器 Q 值跟着负载阻抗的增大而增大,即输出增益在截止频率处有必定的提高。下图是一个滤波器频率呼应曲线:
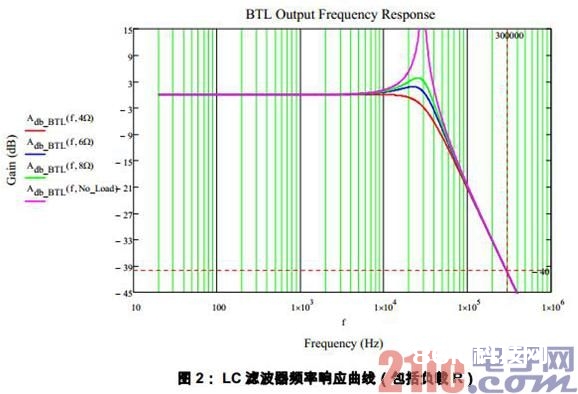
该比如中 L=15uH,C=1uF,截止频率Fn约为 29kHz,在 Class D 的开关频率(约 300kHz)方位供给-40dB 的衰减。在截止频率处,不同的负载阻抗呈现出不同的增益。理论上空载极点情况下增益为无限大,LC 进入谐振状况。
一般来说,由于Fn规划高于 20kHz,截止频率处的增益改动不会影响到音频频带内的幅频呼应。但音频带外的信号会遭到该部分的影响并输出到负载发生功率。若输出信号内正好存在坐落 Fc 处的高次谐波,一起 LC 滤波器 Q 值又很高的时分,高次谐波的功率就会被扩大。有或许超越电流约束阀值而导致过流维护。
由于 LC 滤波器的 Q 值和负载 R 有关,只有当 R 十分大的时分才会呈现高次谐波被扩大的现象。在实践中负载 R 是动圈式喇叭。关于喇叭阻抗 R 和频率的联系鄙人节中给出。
3、动圈式喇叭阻抗剖析
一个一般的动圈式喇叭是由纸盘(Paper Cone)、线圈(Voice Coil)和永磁体(permanent magnet) 组成。喇叭标称的阻抗为直流阻抗,一般为 4W、6W或许 8W。但由于线圈的电感特性以及其他寄生参数,喇叭实践体现出的阻抗曲线(vs 频率)如图所示:
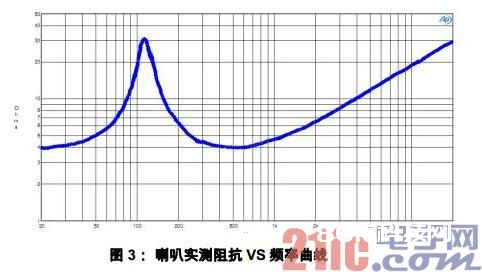
从曲线可看出,该喇叭是一个 4W的喇叭。有一个坐落 110Hz 左右的谐振点。 从 500Hz 开端喇叭即呈现显着的电感特性,阻抗跟着频率的增加而继续增加。可见喇叭阻抗的标称值是其直流特性,跟着频率喇叭阻抗会大幅度改动。在 LC 的截止频率约30kHz 左右喇叭阻抗现已远远大于其标称的直流阻抗。图 3 的比如中,其 30kHz 的阻抗大约在40Ω 邻近。
3.1 动圈式喇叭阻抗模型
动圈式喇叭的阻抗特性能够运用图 4 中的等效电路模型来模仿(等效电路模型的详细剖析请拜见引证 2)。其间:
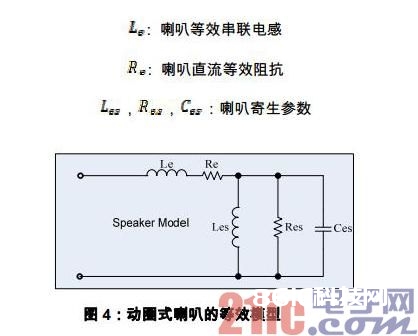
3.2 ZOBEL 补偿网络
实践喇叭的高频阻抗由于线圈电感而呈现随频率增高而上升的趋势,由此导致了 LC 滤波网络的高 Q 值。ZOBEL 是和喇叭并联的阻容网络,它能够用来补偿喇叭的理性而按捺喇叭阻抗的抬升。如图 7 所示,ZOBEL 网络有电阻 和电容 组成。核算公式为(拜见引证 3):
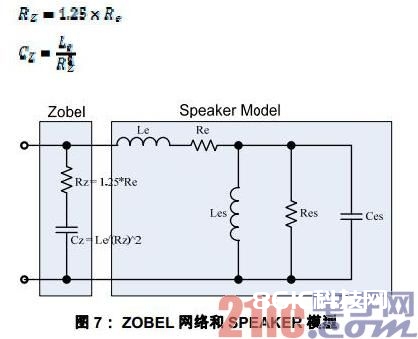
以第 3 节的喇叭参数为例核算得出 和 。图 8 是参加 ZOBEL 网络前后的喇叭阻抗曲线比照。可见 ZOBEL 网络的效果很显着,将高频部分的阻抗提高约束下来,保持在邻近。这样就能约束 LC 滤波网络的截止频率邻近的 Q 值。然后不会发生高次谐波的过流维护问题。
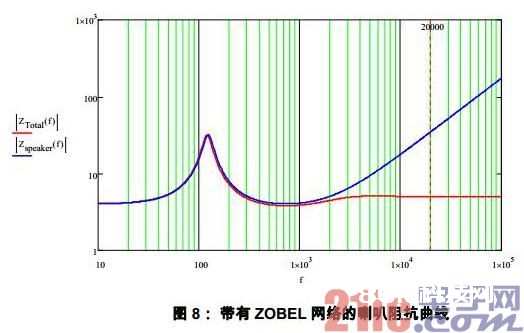
4 、现象剖析及处理方案
归纳上述理论剖析,关于高次谐波过流维护的现象剖析及处理方案如下:
一般在 Class D 功放路规划时会考虑到 20Hz-20KHz 音频带宽内的电信号的频率呼应。确保在20Hz-20KHz 内每个频率点的输出功率均不会超越额外值。一般老化测验时选用的是 1KHz 的规范正弦波,此刻喇叭作业在额外阻抗邻近(本文比如中,约为 4.2ohm)。
可是若输出信号的频率超越 20kHz 即输出含有很多谐波时。就会有坐落 LC 滤波器截止频率(谐振频率)邻近的高频信号。若 LC 滤波器的 Q 值又十分高,则会发生高频谐波被扩大并导致过流维护的问题。
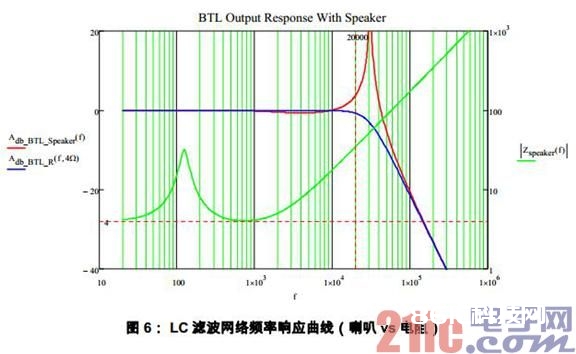
LC 滤波网络的 Q 值与负载阻抗有联系,从第三节已知喇叭在截止频率邻近的阻抗一般很高,则滤波器的 Q 值很大。图 6 是将实践的喇叭阻抗曲线和 LC 滤波器的频率呼应曲线兼并后的成果。
可见当负载为纯电阻 4W时, LC 滤波网络在截止频率处 Q 值较低,没有任何扩大效果。而接入喇叭后,LC 滤波网络在截止频率处发生大于 20dB 的增益。这便是导致高次谐波过流维护的根本原因。
综上所述,关于第一节给出的高次谐波过流维护的现象弥补剖析如下:
l 问题机器在 1KHz 规范音频信号输出功率并未超越最大输出功率。
剖析: 由于该维护现象发生在 LC 滤波网络截止频率邻近,在 20Hz~20kHz 范围内的功率输出正常,并不会出发过流维护。
l 播映高频成分较多的歌曲较简单呈现维护。
剖析:高频成分较多的歌曲内容简单发生坐落 20kHz~40kHz 范围内的谐波能量,正好触发 LC 滤波网络截止频率处的高次谐波过流维护。
l 运用水泥电阻代替喇叭作为负载,维护现象消失。
剖析:该类高次谐波过流维护和喇叭高频呈现的高阻抗有联系,若运用纯电阻代替喇叭则不会呈现该类维护。
l 减小,或许去掉输出 LC 滤波器的电容,维护现象消失。
剖析:LC 滤波器的截止频率方位被改动,减小电容将截止频率推到 40kHz 以上,一般该方位的谐波重量十分小,不足以引起过流维护现象。去掉电容 LC 滤波器不存在,也不会发生维护问题。
4.1 处理方案
1. 减小 LC 滤波器网络的电容 C 值:
减小 LC 滤波器网络的电容 C 的值能够增大 LC 滤波器的截止频率。使得截止频率远大于高次谐波或许到达的频率。一般将电容值减小 5 倍以上即可有用按捺高次谐波过流维护的问题。
长处:无需修正电路,只需求修正参数值。
缺陷:LC 网络滤波效果变差,开关纹波增加,EMI 有或许恶化。
留意:不主张直接去掉滤波电容。否则会导致 Class D 开关纹波输入到喇叭,增加损耗和恶化 EMI。
2. 增加 ZOBEL 网络:
长处:有用按捺喇叭的高频阻抗抬升,处理高次谐波过流问题。一起能够均一化中高频呼应,对高频听感有改进。
缺陷: 需求增加外围%&&&&&%,电容数值较大,引荐运用无极性薄膜电容。
留意: 若仅仅为了处理高次谐波过流问题,ZOBEL 网络的%&&&&&%可小于核算值,一般只需到达阻抗按捺的效果即可。
5 、总结
高次谐波过流维护是一种特别的过功率现象,在电路规划完全正确,惯例功率测验未超越额外功率的前提下,该种维护问题较为荫蔽。本文结合 LC 滤波电路的频率呼应和动圈式喇叭的阻抗频率特性,剖析了 Class D 谐波过流维护的原因并给出了处理方法。