组合逻辑电路的定义
对于一个逻辑电路,其输出状态在任何时刻只取决于同一时刻的输入状态,而与电路原来的状态无关,这种电路被定义为组合逻辑电路。
组合逻辑电路的一般框图如图
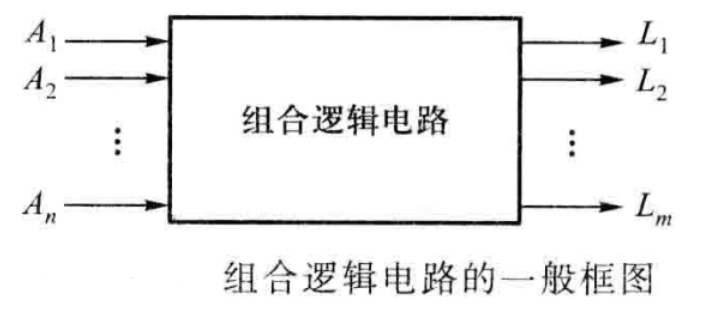
其输出与输入之间的逻辑关系可用如下的逻辑函数来描述,即

组合逻辑电路的结构具有如下的特点:
(1)输出、输入之间没有反馈延迟通路;
(2)电路中不含具有记忆功能的元件。
【注意】:所谓记忆单元,指的是第五章里提到的锁存器之类的器件。
组合逻辑电路特点是任意时刻的输出仅仅取决于该时刻的输入,与电路原来的状态无关。具体来说,组合逻辑电路的输出是由输入信号经过逻辑门电路后得到的,不包含存储元件。
组合逻辑电路的分析方法主要包括:
根据给定的逻辑电路,写出输出函数的逻辑表达式。
进行表达式的变换与化简,直接利用公式或定理对表达式进行变换,也可通过卡诺图的方法进行化简。
根据表达式列出真值表。真值表能直接反映出输入变量和输出结果之间的逻辑关系,它直观地描述了电路的逻辑功能。
对给定电路的功能进行逻辑描述。
常用的组合逻辑电路包括:二进制普通编码器、BCD普通编码器、优先编码器等。组合逻辑电路的应用非常广泛,如计算机的CPU内部、各种数字控制系统、电子仪表、电子通讯等领域的数字处理中。
组合逻辑电路的分析方法
分析组合逻辑电路的一种常用方法是使用真值表或卡诺图。以下是这两种方法的简要介绍:
1. 真值表方法:
– 首先,列出输入端口和输出端口的所有可能值组合,构成真值表。
– 对于每个输入组合,确定对应的输出值。
– 根据真值表中的输出值,找出逻辑门的逻辑运算规则或布尔表达式。
例如,对于一个有两个输入端口和一个输出端口的逻辑门,可以通过真值表列出所有可能的输入组合,然后找出对应的输出值。最后,我们可以根据真值表中的输出值得出逻辑门的逻辑规则。
2. 卡诺图方法(Karnaugh Map):
– 对于每个输入端口,构建一个表格,并将所有可能的输入组合填入表格中。
– 分析表格中每一个组合对应的输出值。
– 根据卡诺图中相邻的1(或0)的分组情况,找出逻辑门的简化布尔表达式。
卡诺图是一种直观且有效的方法,它将二进制数的输入组合和逻辑门的输出用方格表示。通过观察卡诺图中相邻的1(或0)的分组,我们可以识别出逻辑门的简化布尔表达式,以减少逻辑门的数量和简化电路的复杂度。









