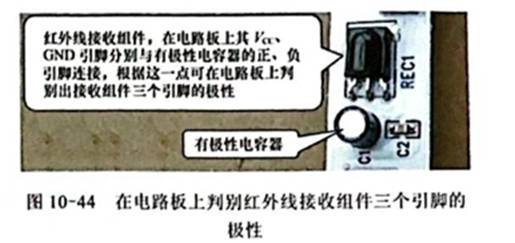
在电子电路规划过程中,负反应的引进让体系变的愈加“听话”,可是,在运用负反应的过程中,也有潜在的不安稳性:当规划的体系满意必定条件时,规划的体系就会变得不那么“听话”,乃至变得振动起来。为了找到负反应线性体系的安稳性,本文对要害点进行剖析。
为剖析体系的安稳性,首要需求知道两个概念:增益交点和相位交点。所谓增益交点,望文生义,便是使环路增益为1的频率点;相位交点是使环路增益的相位为-180°的频率点。这两个频率点在坚持体系的安稳性中,起到重要的效果。在安稳的体系中,增益交点通要比相位交点靠前:

在图1中,增益交点在相位交点之前,满意体系安稳的条件,这样的体系变得安稳,而图2中增益交点在相位交点之后,则体系就变得不安稳。
为什么这么说呢?因为这便是十分闻名的“巴克豪森判据”(Barkhausen’s Criteria)。因而,负反应的引进便是为了战胜这样两个要素。
由此能够看出,一个体系的波特图对判别一个体系的安稳与否有着重要的效果。假如规划出了如图2的体系,明显不安稳,可是能够经过对体系的反应回路调整和补偿,将体系的增益交点出现在相位交点之前,那么,体系就会变得安稳了。
写到这儿,信任不少电子工程师对波特图的运用有了更深入的知道,有爱好的朋友参阅下我之前写的文章赏识波特图的魅力,在这儿我要着重一点,在画波特图的相位图时,需求找好三个要害点:
①关于零点频率ω,在0.1ω处,相位图开端下降;
②在ω处,相位图的经过了大约+45°的相移;
③在10ω处,相位图经过了大约90°的相移;
为阐明这点,现以一RC低通滤波器为例阐明:

其传递函数为
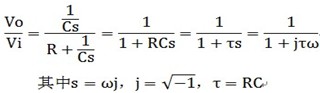
其相位图如图4 所示。
波特图能够大约剖析体系安稳性,在规划过程中,假如体系不杂乱,能够以表达式的方式表达出极点,那么,也能够在复平面中检查体系的安稳性。(因为传递函数长用拉普拉斯改换,引进拉普拉斯算子s,这让我深深理解大学学习复变函数的重要性)。
关于复平面,图5,

若极点落在右半平面,则体系是不安稳的,若在原点处,体系也有或许出在振动状况。也便是说,只要一切的极点都落在左平面内,体系才干变得安稳。(这时,你能想起来大学老师教你的复变函数的一个使用了吧)。
例如若一极点的方位为1+J3,则体系不安稳,若极点方位在-1+j3,那么便是安稳的。所以,在规划体系时,要将一切的极点都落在复平面的右半平面。