一种永磁同步电机失磁毛病滑模调速办法

　　目云奎，陈  玄（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）
　　摘  要：针对怎么改进永磁同步电机(PMSM)操控功能，选用一种依据永磁磁链在线观测的滑模调速办法。首要，选用依据滑模变结构操控的速度环操控模型，剖析永磁磁链对电机带负载才能的影响。然后，在磁场同步旋转坐标系中结构永磁同步电机的新式磁链观测情况方程，经过龙伯格观测器离隔观测器中电机速度改变对观测器差错方程形成的影响，凭借Lyapunov稳定性理论对观测器的稳定性加以证明，依据滑模变结构等值操控原理结构出永磁磁链算式。最终，经过仿真验证了该办法的可行性。
　　关键词：永磁同步电机；滑模调速；永磁磁链；龙伯格-滑膜观测器

　　0 导言

　　沟通永磁同步电机因优异的功能在现代沟通传动范畴得到广泛的使用。永磁同步电机 (permanent-magnetsynchronous motor ,PMSM）永磁资料受外部磁场环境以及温度改变的影响而导致失磁，下降电机操控功能，严峻时电机或许直接作废。针对PMSM受失磁影响而导致操控精度下降的问题，国内外许多学者打开了很多研究工作，文献^[1]在电机转速恒守时，使用RLS算法对四个电气参数进行辨识，文献^[2]在神经网络在线辨识算法中结合最小均方值收敛辨识出电感磁链等参数，文献^[3]把离线估算出的定子电阻用于神经网络辨识器，对转子磁链等参数进行在线辨识，然后使用在线辨识的参数进一步更新定子电阻值，因为存在离线辨识导致该办法难以满意实时性要求过高工况，文献^[4]选用多智能体蝙蝠算法对永磁同步电机多个参数进行辨识。文献^[5-6]为了过滤掉辨识进程中噪声信号，选用扩展的卡尔曼滤波器辨识电机参数，但核算进程较为杂乱。文献^[7]剖析欠秩问题的实质，经过自适应律得到永磁同步电机的速度和永磁磁链。
　　永磁同步电机运转时永磁磁链遭到外部环境的影响而产生改变，然后导致永磁磁链产生失磁，从而影响到滑模调速操控功能。文献^[8]依据指数趋近律进行滑模调速操控，改进了永磁同步电机操控功能。文献^[9]使用积分滑模改进速度环操控，得到必定的作用。文献^[10]选用的新式趋近律与分数阶操控相结合规划速度操控器以减小体系的颤动性。
　　针对传统速度调理办法没有考虑到永磁磁链改变对永磁同步电机带负载才能的影响。本文使用滑模变结构操控与龙伯格操控器相结合的办法对永磁磁链进行重构，重构参数反响到速度环中进行调理，从而确保产生失磁工况时永磁同步电机的带负载才能。经过仿真对该办法的可行性进行验证。
　　1 PMSM数学模型

　　在同步旋转d-q坐标系下PMSM的电压方程为^[11]：

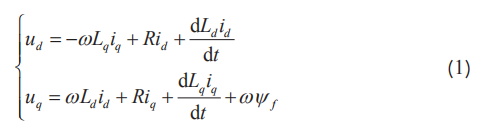
　　式中， u_d 、u_q —d、q电压； 

　　i_d 、i_q —d、q轴电流；

　　L_d、L _q —d、q轴电感； 

　　R —定子电阻； 

　　ω —转子电角速度； 

　　ψ _f —转子永磁磁链。
　　选用 i_d = 0 的矢量操控办法，则PMSM电磁转矩方程为：

　　式中， n_p —电机极对数。
　　永磁同步电机转矩平衡方程为

　　式中， J —转动惯量； 

　　T_L —负载转矩。
　　PMSM永磁体磁链矢量的幅值产生改变，如图1所 示^[12]。PMSM永磁体磁链矢量的初始值将会由 ψ _f 改变到 ψ ' _f 。

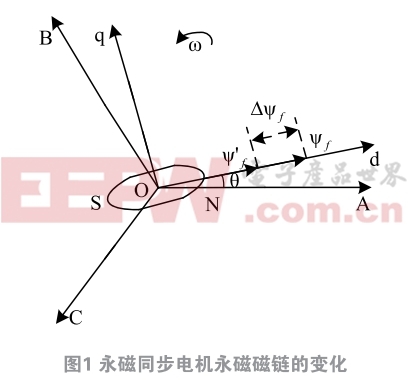
　　为便于龙伯格-滑模观测器规划，由式( 1 )可得PMSM电压方程：

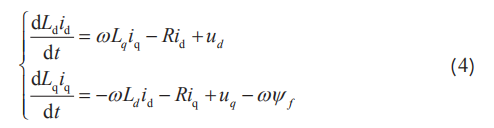
　　令L_di_d=X₁ ，L_qi_q=X₂

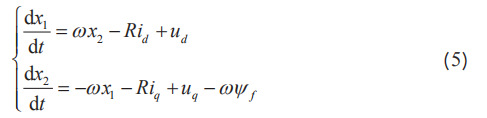
　　界说直轴电枢反响磁链为L_di_d=X₁，交轴电枢反响磁链为L_qi_q=X₂。 

　　将 x₁ 和 x₂ 作为选定的情况矢量，由式(5)构建PMSM在d-q坐标系下的磁链重构情况方程：

　　式中，情况矢量 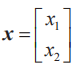，体系输入矢量 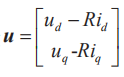，永磁磁链矢量 。
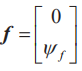　　情况方程系数矩阵：

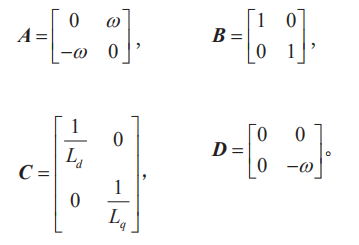
　　2 滑模观测器规划

　　2.1 速度环规划

　　令转速差错 e =ω*_e-ω_e ，由式(3)得

　　式中， e —转速差错的改变率^[13]：

　　由式(2)、式(7)得

　　式中， e—转速差错的二阶导。
　　由式(7)和式(8)可得永磁同步电机在相空间的数学模型为

　　设切换函数为

　　式中， c 为大于0的常数。
　　规划操控率为

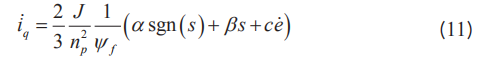
　　滑模操控稳定性推导见文献^[13]。
　　2.2 磁链重构

　　为了得到PMSM的磁链重构值，依据式(6)电机模型，结构式(14)龙伯格-滑膜观测器：

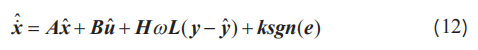
　　式中， k sgn (e) 是滑模操控项， k 是待规划矩阵，^表明观测值， sgn (⋅) 是符号函数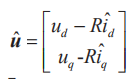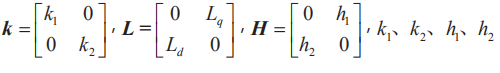，均为待规划实数。
　　取情况差错

　　由式(6)与式(13)可得观测器差错方程为：

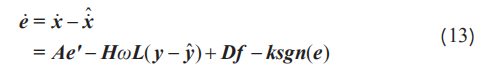
　　式中，

　　挑选式(15)正定函数作为Lyapunov函数，证明式(13)

　　所规划观测器的稳定性：

　　对(15)求导得：

　　由 式 (16) 可看出 ， 当规划 A=Hω 时 ， 即规划  ，观测器中 ω 的改变对观测器差错方程形成影响可被离隔。进一步由式(16) 得

　　式 (18) 中 k 的取值 ， ， 其 中 是大于零的常值矩阵，K₃= min{K₁,K₂ } 。
　　只需规划 ，则可得出：

　　由Lyapunov稳定性理论可知，磁链观测器收敛作用较好。
　　滑模等值原理^[14]表 明 ， 体系抵达滑模面后 ，e=e=e'=0 ，所观测的磁链参数收敛到实践值邻近。由式(14)可得：

　　对式(19)进行打开，代入相应参数可得永磁磁链算式：

　　用Sigmoid函数 F(e) 代替传统的开关函数以便减小滑模运动的颤动性^[15]。其函数办法为：

　　式中，a>0，Sigmoid函数的斜率用其来进行调整。因此结构失磁工况下永磁磁链核算式

　　将式(22)带入式(12)，由式(2)、式(3)知，当产生失磁工况时，可经过调理 iq 来确保电机快速呼应。
　　3 仿真与剖析

　　图2为失磁工况滑模调速操控体系框图，首要包含电流调理器模块、速度调理器模块及情况观测器模块等。使用龙伯格-滑膜观测器对永磁同步电机进行永磁磁链重构，重构的参数用于速度环调理。滑模观测器参数设置为： λ =150 ， ε = 870 ， c = 3850 ， k₁ = 2280 ， k₂ =1310 ， a = 2.5 ， h₁ =1 ， h₂ = −1 。仿真中所用的PMSM参数如表1所示。电机操控选用 i_d = 0 的矢量操控战略。

　　仿真在电机失磁工况下进行，磁链在0.1 s时，由 0.175 Wb变为0.150 Wb。

　　为了验证所结构的磁链观测器的鲁棒性，分别在PI调速操控和滑模调速操控两种情况下运转，且在0.08 s 时，电机速度由300 rad/s加快到380 rad/s。仿真成果如图2(a)、图2(b)，成果显现在两种操控下，规划的观测器能很好地盯梢方针参数，鲁棒性较好。

　　图3是PI调速操控下 i_q 轴电流、电磁转矩以及转速呼应时刻曲线。图4是滑模调速操控下 i_q 轴电流、电磁转矩以及转速呼应时刻曲线。由图3(a)、3(b)和图4(a)、 4(b)能够看出，分别在0.05 s和0.1 s时，负载转矩由0 N.m突加为2 N.m、永磁体磁链产生失磁时，PI调速操控下， i_q 轴电流以及电磁转矩呼应较慢。由图3(c)、4(c)可知滑模操控下，转速能够快速呼应。

　　由图(3)、图(4)知，当产生失磁工况时，应及时观测出磁链，并反响到速度环，以确保电机带负载才能不变，仿真成果表明，磁链观测器具有较高的鲁棒性，以及在失磁工况下滑模调速操控具有显着优越性。
　　4 定论

　　本文提出了永磁同步电机新式情况方程模型与滑模变结构以及龙伯格观测器相结合办法，离隔了电机速度对观测器差错方程的影响，给出磁链参数观测值，然后把观测所得观测值反响到滑模调速操控中，以确保电机快速呼应。鲁棒性强，滑模变结构观测器参数易于挑选。仿真成果对该办法的可行性进行了验证。
　　参考文献

　　[1] ICHIKAWA S,TOMITA M, DOKI S, et al. Sensorless controlof permanent-magnet synchronous motors using onlineparameter identification based on system identificationtheory[J]. IEEE Transactions on Industrial Electronics, 2006,53(2): 363-372.
　　[2] 谷鑫,胡升,史婷娜等. 依据神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技能学报,2015,30(6):114-121.
　　[3] LIU Kan, ZHANG Qiao, CHEN Jintao. Online multiparameterestimation of nonsalient-pole PM synchronous machineswith temperature vatiation thracking[J]. IEEE Transaction onIndustrial Electronics, 2011, 58(5):1776-1788.
　　[4] 吴忠强,杜春奇,李 峰等. 依据蝙蝠算法的永磁同步电机健康情况监测[J]. 仪器仪表学报,2017,38(3):695-702.
　　[5] BOILEAU T, NAHID-MOBARAKEN B, MEIBODY-TABAR F.On-Line Identification of PMSM Parameters: Model-Referencevs EKF[C]//Industry Applications Society Annual Meeting,2008:1-8.
　　[6] JARAMILLO R,ALVAREZ R,UR DENAS V,et al.Identificationof induction motor parameter using an extended Kalmanfilter[C]//1st International Conference on Electrical andElectronics Engineering,2004:584-588.
　　[7] 韩世东,王应喜,邢益超等. 依据永磁磁链在线辨识的永磁同步电机无速度传感器操控[J]. 电机与操控使用, 2018,45(1):46-50.
　　[8] 崔茂振, 张昌凡, 朱剑. 永磁同步电机滑模调速操控及其完成[J].电子丈量与仪器学报, 2012, 26(1):84-92.
　　[9] 徐金龙, 张向文, 刘政等. 依据积分型滑模面的无刷直流电机滑模调速操控算法[J]. 微电机, 2015,48(5):61-65.
　　[10] 张文宾,缪仲翠,余现飞等. 依据改进型滑模观测器的永磁同步电机分数阶微积分滑模操控[J]. 电机与操控使用, 2018, 45(7):8-14.
　　[11] 曹艳玲,文彦东. 永磁同步电机直交轴电感参数离线丈量办法[J].微电机,2016,49(2):41-64.
　　[12] 肖曦,张猛,李永东. 永磁同步电机永磁体情况在线监测[J].我国电机工程学报, 2007, 24(27)：43-47[13] 赵越, 刘斌. 依据滑模变结构的内置式永磁同步电机弱磁矢量操控[J]. 信息与操控, 2017,46(4):428-436.
　　[14] 邱忠才,郭冀岭,王斌等. 依据卡尔曼滤波滑模变结构转子方位观测器的 PMSM无差拍操控[J]. 电机与操控学报,2014,18(4):60-71.
　　[15] 赵凯辉, 陈特放, 张昌凡等. IPMSM非奇特快速终端滑模无速度传感器转矩操控[J].仪器仪表学报,2015, 36(2):294-303.

　　本文来源于科技期刊《电子产品世界》2020年第02期第36页，欢迎您写论文时引证，并注明出处。