热连轧体系大多选用活套设备,经过其缓冲效果来吸收咬钢进程中构成的套量,并坚持安稳的小张力操控.在实践运用中,张力的设定值既不能过大,也不可以过小.张力过大对带材质量有影响;张力过小会使活套体系不安稳,不利于安稳轧制.
传统的活套操控是经过调整上游机架轧辊速度使活套高度维持在设定值邻近,经过操控活套电机力矩使机架间张力安稳.在这种操控战略中,活套高度与张力操控是彻底独立进行的,没有考虑二者之间存在的耦合联系.而实践状况是活套高度改变时,机架间张力也发生改变,反之亦然.即活套高度与张力体系是一个典型的双输入,双输出耦合体系.此外,活套操控体系还与其他操控体系(如AGC体系、机架间的喷水体系)之间存在着相互效果,这使得活套操控比较杂乱消除耦合联系,使活套安稳作业.进步产品的尺度精度,已成为活套操控的一个重要课题.
为了完成活套高度与张力体系解耦操控,需树立其动态数学模型.在鞍钢1700热轧厂,对F3,F4机架间活套耦合体系建模,选用FPGA器材进行了根据BP神经网络份额、积分、微分参数自学习的PID操控器的规划,为先进的操控战略在热轧现场运用奠定了根底.
1 体系建模
活套体系对错线性、时变的,要想获取其准确的数学模型是不或许的.在进程操控中,大多数运用线性时不变模型来描绘.当进程违背平衡点的改变很小时,操控体系的动态行为就可以用线性时不变模型来描绘.这样可防止很多非线性方程联解的困难,即完成对非线性体系线性化处理.这儿只考虑F3压下、F4不动作时对体系建模.
1.1 活套张力体系建模
张力增量方程为 
1.2 活套高度体系建模
因为活套臂的动作,发生角加速度,即当活套处于动作进程中,除了接受张力矩MT、重力矩外MW、活套电机实践上还将接受一个动力矩,打破原有的平衡联系,使张力矩发生改变.因为实践的活套组织有减速设备,传动比为GR,电机转速为n,则整个活套电机输出力矩为: 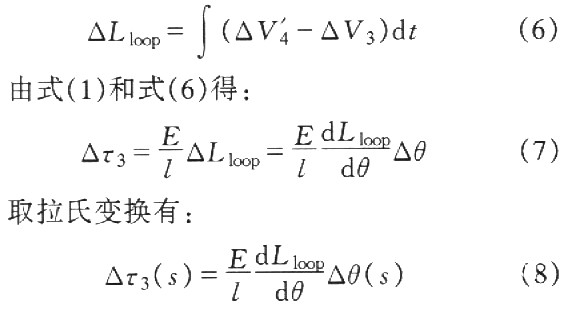
将主电机与活套电机近似为一阶惯性环节,由式(5)和(13)得到体系的耦合框图1.
活套高度和张力的作业点取为:活套臂升角θ=21°,张应力τ3=4.8N·mm-2,弹性模量E=150N·mm-2,机架间隔l=6m,活套器支点与F3的间隔la=2.2m,活套臂交点离轧制线的间隔ha=0.18m,活套臂全长R=O.796m,活套辊半径r=O.11m,传动比GR=14:1;f3,Ti,Tv,Ki分别为0.082,0.18,0.09,8.25;J=7.85kg·m2;V03,V04分别为3.246m·s-1,4.786 m·s-1:F3机架进口厚度为H=9.44mm,出口厚度为h=5.69mm,作业辊半径R1=0.332m;α,β为F3,F4板带出口、进口与轧制线的视点,在线性作业点(θ,τ3)处线性化处理,相应的非线性函数是: 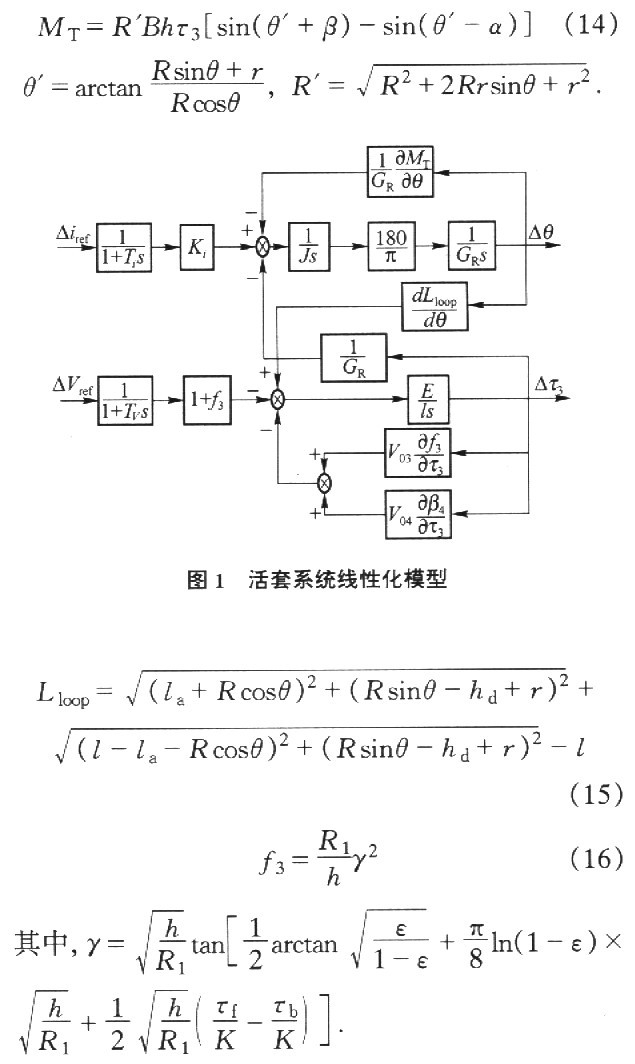
式中,B为板宽,γ为中性角,ε为相对变形程度,K为金属变形阻力,τf为前张应力,τb为后张应力.
可得到: 


应该指出线性化后所得到的传递函数是被控目标的近似数学模型,系数是慢时变的,可作为解耦操控器(经典传函、奈氏办法等)的规划根据.关于绝大多数状况来说,解耦器的增益不该该是常数.假如要到达最优化,则解耦器有必要对错线性的,乃至是适应性的.假如解耦器是线性和定常的,那么可以意料解耦将不完善.在某些状况下解耦器的差错或许引起不安稳.文中选用BP神经网络整定的PID解耦操控器,进行了仿真研讨,详细算法见文献.
2 BP-PID在FPGA上的规划
在结构实践的神经网络运用体系时,必定要考虑到硬件完成问题,特定运用下的高性能专用神经网络硬件是神经网络研讨的最终目标.为此选用FPGA器材进行这项作业,选用数据驱动的脉动阵列并行处理办法,进行了由13个神经元组成的三层(4-6-3)电路规划.因为电原理图规划很直观,因而在顶层选用了电原理图的规划办法,而功能模块则选用VHDL,描绘办法进行规划.
根据上述办法,关于三层BP前馈神经网络硬件规划的体系整体框图见图2. 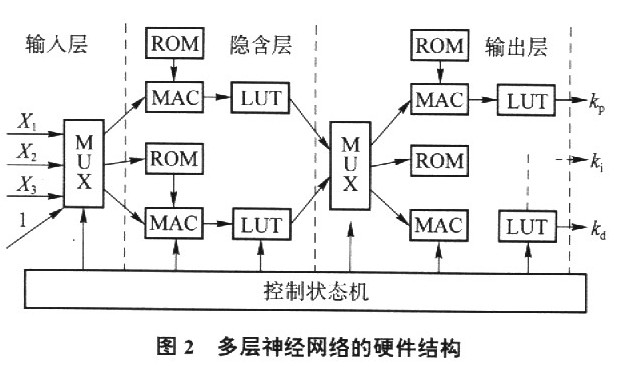
在图2中,X1,X2,X3是神经网络的输入,对应于r(k),y(k),e(k),Y1,Y2,Y3对应于PID操控器的三个可调参数kp,ki,kd ROM模块存储的是每一神经元对应的权值向量(整个神经网络共需对42个权值批改);MAC是神经元的乘累加模块;LUT是效果函数查找表模块;MUX是多路选通器,担任数据流的扇入扇出.从神经元的数学模型可以看出,其最基本也是最杂乱的运算为权值与输入的乘累加运算.脉动阵列结构(Systolic结构)是一种有节奏地核算并经过体系传输数据的处理单元网络.Systolic结构的优势在于它可以用流水线的办法完成矩阵向量乘法,因而这种结构十分合适神经网络的完成;一起,因为其具有模块化及规则化的特征,十分合适用数字VLSI完成为了便于在硬件上完成,考虑到运算杂乱度和速度,运用定点格局的数据,一般来说,16位的定点数是不用弱神经网络才干的最小要求.其他需求阐明的是:关于前馈多层网络,只用于前向传达所需的数据精度一般可小于后向传达所需的精度;选用常用的Wallace树乘法器,其核算速度快,占用面积小;关于FPCA硬件来说,其可完成的运算极为有限,而BP网络中的效果函数对错线性的,是硬件完成的一个难点,例如BP网络中的效果函数为Sigmoid函数;常用的完成办法是查表法,这种办法比较简单,但需求占用较多资源,当需求完成的网络规划较大且精度要求较高时,查表法的完成有很大妨碍;其他可以考虑的完成办法是用多项式去迫临这一非线性函数在硬件完成中,考虑到Sigmoid函数在输入大于必定数值后即进入饱满区的特色,只对原点邻近的函数值进行存储,可节省很多资源并简化问题,其作业效果与非查表办法完成的仿真软件很挨近.神经网络硬件完成的优势主要是速度快,特别当运算量大时,其优越性才干表现出来.在实时操控中,特别是在高速轧制进程中,先进的操控算法其运算的快速性是尤为重要的,是在工业操控中可以运用的条件学习算法的硬件完成面临着两个难题,一是数据流操控杂乱,二是数据精度对收敛性的影响.关于数据精度对收敛性的影响,为简化起见,点评函数挑选为差错的平方和.
将式(17)离散化,实践的活套臂长度为796mm,在线性作业点处对应的套高285 mm,对活套高度附加15%左右,即起伏为40mm的阶跃扰动信号.神经网络的结构4-6-3,加权系数初始值取区间[-0.5,0.5]上的随机数,输入形式选为r(k),y(k),e(k),1.学习速率η=0.34,惯性系数α=0.06.解耦后的带钢张力改变曲线如图3所示. 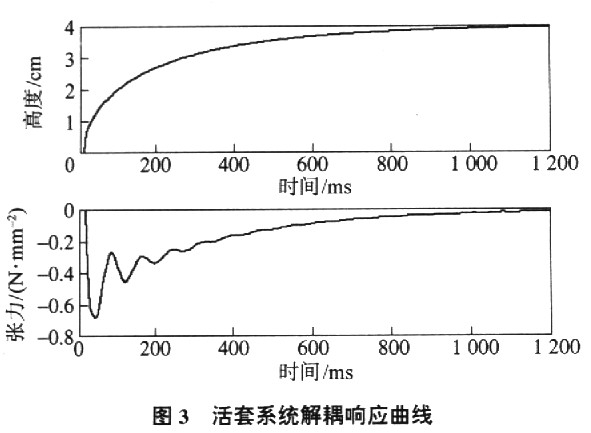
仿真结果表明,根据上述的操控战略,体系在满意活套高度增量设定的一起,活套张力动摇较小,在500ms时张应力的改变为-0.2N·mm-2在800ms时张应力的改变为-0.05N·mm-2,然后完成了活套高度与张力耦合体系的解耦操控.
3 结语
如何将神经网络的操控算法固化到专用的芯片上,以处理高速轧制进程与杂乱操控算法核算耗时的对立,是实践热轧现场可以运用的条件.根据上述剖析,本文规划了相关的仿真软件,并用FPGA完成了一个选用BP算法可以进行片上学习的前馈多层网络模型.