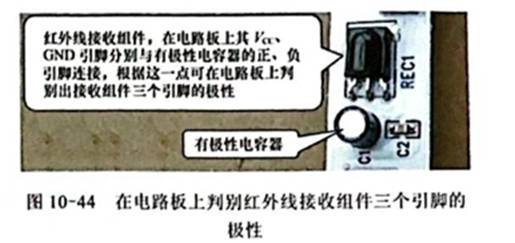
直方图(Histogram)也叫柱状图,它是用一系列宽度持平、高度不等的长方形表明数据的图,如图1(a)所示,长方形的宽度表明数据规模的间隔,长方形的高度表明在给定间隔内的数据数量。在计算学上这是很常用的用来表明样本各组概率散布的一种直观的图表。假如样本容量获得满足大,分组的间隔获得满足小,柱状的直方图就会变成曲线图(图1 b)。这条较为滑润的曲线便是样本整体的密度曲线。它提醒了样本的散布规则。
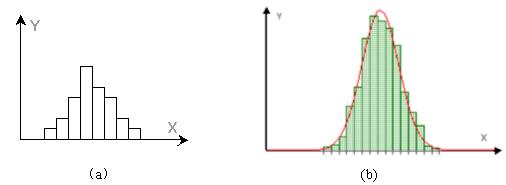
图1什么是直方图
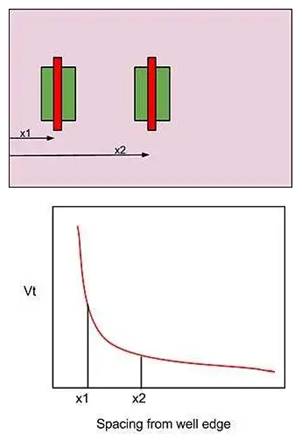
直方图描绘了数据或许参数值在一个确认规模内呈现的概率(如图2),直观的显现了参数的动摇状况。在用示波器对波形参数进行丈量时,咱们能够使用直方图,依据丈量成果的计算剖析确认产品的一些要害目标,经过许多数据样本的数值规模和散布状况能够验证产品的功能和质量并辨认和确诊一些间歇性的问题。尤其是关于随机事情(如噪声或颤动)的了解,它是一个很好的东西。因为在颤动剖析中一切信号均包含有随机成分的颤动,因而有必要选用计算的手法来剖析和检定颤动,而直方图便是最常用的计算剖析东西,所以说直方图是颤动剖析的根底。
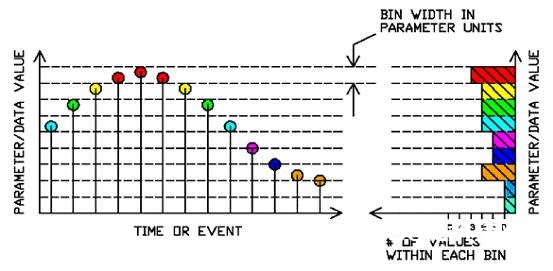
图
2怎么得到直方图2怎么得到直方图
描绘直方图的主要参数有均匀值(mean)、标准偏差(standard deviation)、样本峰-峰值和样本总量。力科示波器包含了一切这些计算参数。
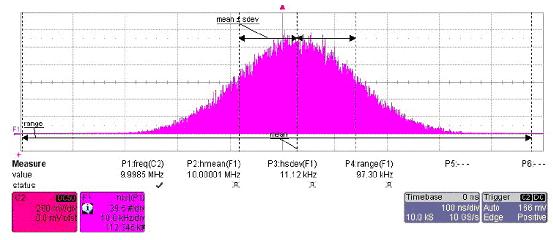
图
3示波器中的直方图与直方图参数3示波器中的直方图与直方图参数
均匀值是测得一切值的算术均匀,表明丈量值的最佳预算成果,即图3中的“mean”。
标准偏差是丈量值违背均匀值的均匀量,常用σ表明。它决议了直方图的“胖瘦”,标准偏差越大,离散程度越大,图形就越胖。在力科示波器顶用“mean±sdev”表明直方图的标准偏差,假如均匀值为0,则标准偏差等于参数的均方根值(rms)。
直方图曲线描绘了某个概率散布的概率密度函数(%&&&&&%),在数学模型中求这个概率密度函数定积分,即求图1(b)中赤色曲线与X轴围成的面积,其成果为1。在实践使用中,许多变量都有近似于高斯散布的概率散布,则其约68%的数值散布在距均匀值±1σ之内的规模,约95%数值散布在间隔均匀值有±2σ之内的规模,以及约99.7%数值散布在间隔均匀值有±3σ之内的规模(图4)。

图
4高斯散布的标准偏差4高斯散布的标准偏差
最大值、最小值和峰-峰值:最大值和最小值一般指丈量过程中实践观察到的值,峰-峰值(Range)则是最大值与最小值之差。需求指出的是,对确认性信号而言,即使是在相对较短的丈量区间内测得的,这些值仍很可能等于其实践的真正值。但对具有高斯散布的随机信号而言,理论上最大值和最小值是没有边界的,因而观察到的峰-峰值一般会跟着丈量时刻(丈量样本)的增加而增加。
样本总量是直方图中包含的丈量总数,图3中直方图的标签F1指明晰这个值,即列表底部的数值。在这一丈量实例中,样本总量是频率参数测得的112,345个值。