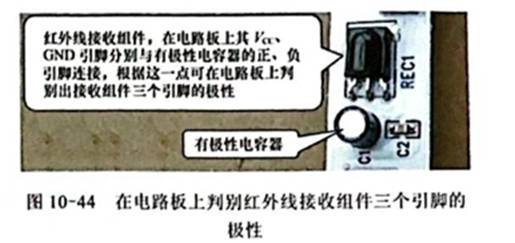
1简介
颤动是实践信号的一组边缘与抱负信号之间的差错（兔子：说白了，颤动便是实践状况和抱负状况不一样，不同越大颤动越大）。时钟信号的颤动一般由体系中的噪声或其他搅扰要素引起。影响要素包含热噪声、电源改动（动摇）、负载的状况（负载也能够反过来影响时钟信号）、设备噪声和挨近电路耦合进来的搅扰。
2颤动的分类
颤动能够通过许多办法丈量（不同办法丈量到的颤动被别离加以界说），以下是首要的颤动分类：
1. 周期颤动（Period Jitter）
2. 相邻周期间的颤动（Cycle to Cycle Period Jitter）
3. 长时刻颤动（Long Term Jitter）
4. 相位颤动（Phase Jitter）
5. 单位时刻距离颤动（TIE，Time Interval Error）
2.1周期颤动
周期颤动是时钟信号的实践周期长度与抱负周期长度之间的差错，丈量样本为数目不定（随机）的一组周期。假如给定必定数意图单个时钟周期，咱们就能够通过丈量每个周期的长度并核算均匀的周期长度，以及这些时钟周期的规范差和峰峰值（peak-to-peak value）。这儿所说的规范差和峰峰值也别离被称为RMS颤动和Pk-Pk周期颤动。
许多文献将周期颤动直接界说为被测时钟周期与抱负周期之间的差错。可是实在状况下很难对抱负周期进行量化。假如咱们用示波器调查一个标称100MHz的晶振，测得的均匀时钟周期却或许是9.998ns，而不是抱负的10ns。所以退而求其次，一般将均匀周期作为抱负周期看待（兔子：由于实践周期都是在抱负值周围依照必定规则散布的，假如丈量时刻满足长，得到的均匀值就能够十分挨近抱负值）。
2.1.1周期颤动的运用
周期颤动关于核算数字体系的时序裕量十分有用。假定在一个依据微处理器的体系中（上升沿采样），处理器要求1ns的数据树立时刻（即数据需求在时钟上升沿1ns前坚持稳定有用）。当时钟的某个周期颤动为-1.5ns时，上升沿会出现在数据有用之前，如此处理器将会收集到过错的数据。如图1所示：
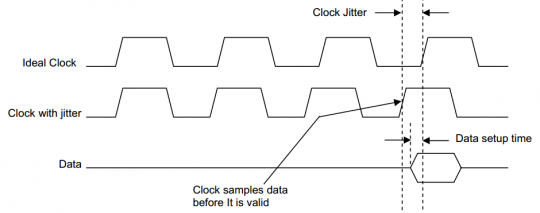
图1时钟颤动形成的数据树立过错
相似的，假如另一个处理器需求2ns的数据坚持时刻，可是时钟某一个周期的颤动是+1.5ns，那么实践有用的数据坚持时刻只要0.5ns，处理器也会采到过错的数据。如图2：
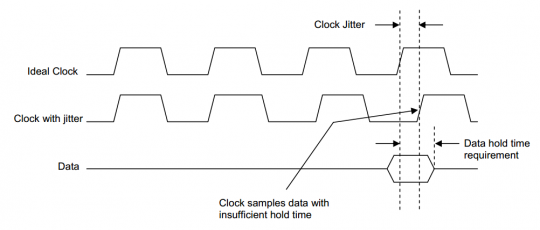
图2时钟颤动形成的数据坚持过错
2.1.2由RMS颤动核算Pk-Pk颤动
由于时钟的周期颤动是随机的，并遵照高斯散布。因而周期颤动彻底能够用统计学中的均方根（RMS ，Root Mean Square，甭说不会算）来表明，单位为皮秒（ps）。可是呢，峰峰值却和核算树立坚持时刻裕量有更大的联络（峰峰值表明晰最大差错，超越树立坚持时刻要求，数据采样就有或许犯错）。要将10000个时钟周期的RMS颤动换算成Pk-Pk颤动，可遵照以下等式：
Pk-Pk周期颤动=7.44 x RMS颤动 *等式1
例如：若RMS颤动为3ps，则Pk-Pk周期颤动为7.44 x 3 = ±11.16ps。
等式1其实是由高斯概率密度函数表（PDF ，Gaussian Probability Density Function）推导出来的。比方当样本个数为100时，从统计学的均匀状况来讲，其间 99个会落在有用值周围的±2.327σ规模内，只要1个会落在该规模之外。依据JEDEC规范的要求，某司丈量RMS周期颤动时设定的样本数为10000。
|
样本数 |
σ |
|
10 |
±1.282 |
|
100 |
±2.327 |
|
1,000 |
±3.090 |
|
10,000 |
±3.719 |
|
100,000 |
±4.265 |
|
1,000,000 |
±4.754 |
|
10,000,000 |
±5.200 |
|
100,000,000 |
±5.612 |
|
1,000,000,000 |
±5.998 |
|
10,000,000,000 |
±6.362 |
|
100,000,000,000 |
±6.706 |
|
1,000,000,000,000 |
±7.035 |
表1高斯概率密度函数表（%&&&&&%）
2.1.3周期颤动丈量办法
JEDEC Standard 65B中将周期颤动界说为某一随机数量的时钟周期与抱负周期之间的差错（由界说了一次，生怕咱们忘了）。JEDEC规范进一步地指定了测周期颤动需求丈量10000个信号周期（多一个少一个应该也无所谓吧）。某司引荐的测验过程如下：
1. 丈量一个时钟周期（一个上升沿到下一个上升沿之间）的长度，即一个样本
2. 等候随机个时钟周期
3. 重复1、2两步10000次
4. 通过测到的10000个样本，核算均匀值，规范差(σ)，和峰峰值
5. 重复1-4过程25次，通过这25组成果，核算均匀峰峰值
10000个随机样本核算出的规范差（σ），即均方根（RMS，也有人以为均方根和规范差并非同等）现已很准确了，RMS的差错能够通过如下等式核算：
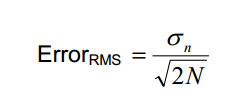*等式2
等式中的σn为样本的RMS，N为样本数。
例如：样本数为10000，RMS差错为0.0071 σn。这种差错是随机的，而且遵照高斯散布，一般用±3 x RMS差错来核算最大丈量差错。
又例如：假如从10000个样本中核算出RMS为10ps，则RMS差错为0.071ps，一切RMS值都会落在10 ± 0.213ps（RMS ± 3 x RMS差错）的规模内。在实践运用中，若只要10000样本，RMS差错能够忽略不计。
Q： 为什么要用均方根来核算峰峰值？
A：必定数量的随机样本就能够准确核算出均方根，可是想要丈量实践的峰峰值却十分困难。由于周期颤动的随机性，样本数量越大则越有或许丈量到落在高斯散布曲线远端的样本，换言之峰峰值随采样数量添加发散，而非收敛。
Q：为什么需求过程5（重复25次）？
A：每丈量10000个样本，就能够算出一个规范差（均方根）和峰峰值。而随机地重复该过程25次，咱们就能够核算很高精度的的均匀峰峰值。这添加了峰峰值丈量的共同性和可重复性。（兔子：便是说每次直接测250000个数据核算出的峰峰值共同性欠好，这样分隔测就好啦？有待验证……）
图3为某125MHz晶振的周期颤动直方图，一起显现了10000个样本中测得的RMS和Pk-Pk颤动。
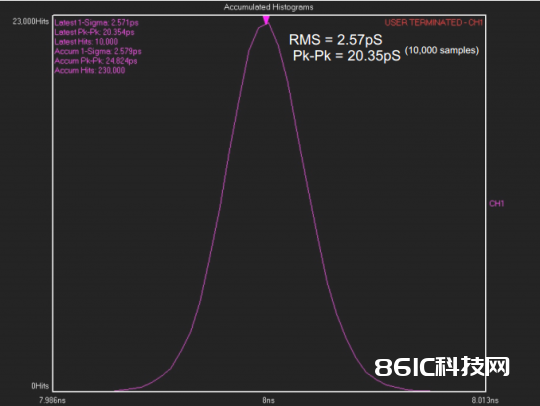
图3 10000个样本的周期颤动直方图
2.2相邻周期颤动
JEDEC 65B规范将相邻周期颤动（C2C，Cycle to cycle）界说为信号相邻周期之间的时刻长度改动，条件也是丈量不定数量（随机）的相邻周期长度差，归纳后得到的成果。JEDEC规范也进一步指定了每个样本集的样本数应该大于或等于1000（便是收集1000对相邻周期）。需求留意的是C2C颤动只重视两个接连周期之间的周期长度改动，并不参阅任何抱负时钟。
C2C颤动一般用峰值表明，有时分也用均方根表明，单位是ps。该参数界说了一个时钟信号的恣意两个接连周期间长度改动的最大值（以上升沿为规范）。此类颤动常被用于体现带有扩频（SSC，spread spectrum clock）特性时钟的稳定性，原因是周期颤动对扩频（频率值会发生改动）很灵敏，C2C颤动则否则。
2.2.1相邻周期颤动丈量办法
1. 丈量某时钟的两个相邻周期的长度：T1和T2
2. 核算T1-T2，取绝对值
3. 等候随机个时钟周期
4. 重复1-3过程1000次
5. 核算标这1000个样本的准差（σ）和峰值，峰值为|T1-T2|的最大值
6. 重复1-5过程25次，核算25个峰值的均匀值
与周期颤动的峰峰值相似，C2C颤动的峰值也是随样本数发散的。第6步用于获取均匀峰值（以添加测验成果的共同性和可重复性）。
图4为某时钟C2C颤动的直方图，这儿颤动峰值为25.66ps（正负峰值21.22ps和-25.66ps中取最大值）。
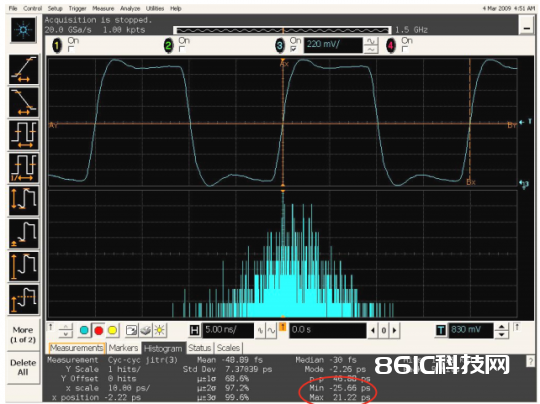
图4 C2C颤动直方图
2.3长时刻颤动
长时刻都懂用于丈量一组接连时钟周期中实践时钟与抱负四种的差异。实践需求丈量多少个周期由运用场合决议。长时刻颤动与周期颤动、相邻周期颤动不同，它表明一段长时刻、接连的时钟信号流中存在的颤动累积效应，因而长时刻颤动也被称为累计颤动。长时刻颤动的典型运用为图片及视频显现、长途遥感勘察及测距仪。
某司引荐的丈量长时刻颤动办法如下（以10000个时钟周期为例）：
1. 丈量10000个周期的总时刻长度，如图5所示
2. 等候随机个时钟周期
3. 重复1-2过程1000次
4. 核算这1000个样本的有用值、规范差和峰峰值
5重复1-4过程25次，取25次峰峰值的均匀值
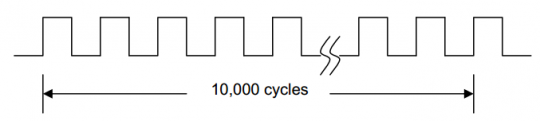
图5丈量10000个时钟周期的总时长
同理，咱们需求通过过程5来战胜峰峰值的无鸿沟散布特性。
2.4相位颤动
相位噪声一般被描绘为在不同频率下的一组噪声值（如-60 dBc/Hz @ 20KHz 和 -95 dBc/Hz @ 10MHz），或许表明为一段接连频率规模内的噪声图。相位颤动则是一段特定频谱中相位噪声归纳的成果，其单位是秒。
关于方波而言，其首要能量会集在载波频率上，但一些能量仍会在载波频率两边的必定频率规模内“走漏”（leaked-out）出去。相位颤动便是与载波频率fc相关的两个指定频率之间的相位噪声能量总和。图6是一个未经滤波的相噪图，暗影区域即表明f1至f2频率之间的相位颤动。
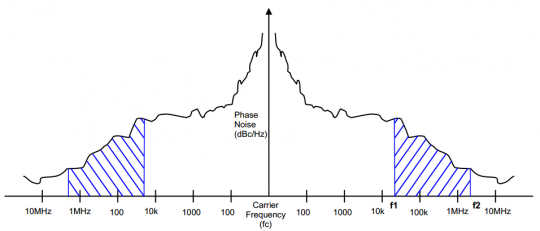
图6相噪图
频率f1与f2之间的RMS相位颤动能够用等式3表明：
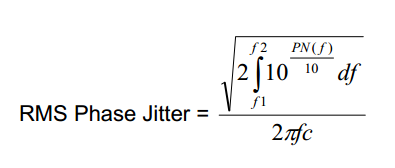*等式3
其间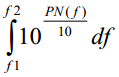
表明fc一侧f1-f2之间的噪声功率。在通讯领域中，通讯接口的发送端 PLL和接纳端 PLL存在带通滤波效，因而在实践状况下咱们需求依据滤波器的特性核算滤波后的RMS相位颤动。以下为常见通讯接口对应带通滤波器的带宽（拐点频率），这些带宽是归纳了发送和接纳端PLL特性得到的成果：
1. 光纤接口： 637 KHz ~ 10 MHz
2. 10GE XAUI接口：1.875 MHz ~ 20 MHz
3. SATA/SAS接口： 900 KHz ~ 7.5 MHz
假定滤波器函数为H(f)，则滤波后的RMS相位颤动能够用等式4核算：
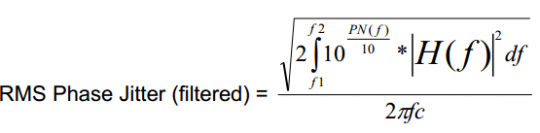*等式4
3单位时刻距离差错
单位时刻距离差错（TIE，Time Interval Error）是指在具有参阅点（兔子：用于参阅的时钟边缘，在该点实践时钟与抱负时钟边缘对齐）的状况下，信号的某个实践边缘与抱负边缘间的时刻差。事实上，TIE是相位噪声在离散时刻域上的体现，单位为秒或皮秒。图7形象地描绘了TIE的根本概念。抱负信号一般是由软件对被测信号的周期进行均匀估量得到的。
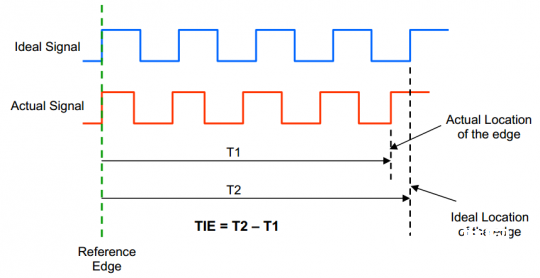
图7丈量单个信号边缘的TIE
3.1制作时域TIE图
图8的最上面一行是一组时钟的的波形，赤色表明周期为1000ps的抱负时钟，黑色表明带有颤动的实践时钟。为了便利表明，只画出了时钟的上升沿。在时钟序列的开端，抱负边缘与实践边缘重合（以此作为参阅点），之后由于颤动，黑色的实践时钟边缘开端跟着时刻漂移，时而抢先时而落后于赤色的抱负时钟。
图中的Clock Period曲线表明所测得黑色时钟的各个周期长度。本例中黑色时钟不是990ps便是1010ps（为了便利了解，抱负化了，和榜首行也不太对的上，将就看吧）。
Period Change曲线则描绘了每个时钟周期与前一个周期的改动量。假如黑色时钟的两个相邻周期长度相同，那么Period Change曲线就会坚持平整，反之就会发生改动。例如：……（兔子就不举例了都能看懂）总而言之该曲线描绘了时钟周期的改动。
TIE曲线则记录了抱负边缘和实践边缘之间的累计差错。此一例中，TIE曲线开端时向下添加，这是由于开端的四个时钟周期里每个实践周期都比抱负周期长度要少10ps。在累积了-40ps的颤动差错后，曲线从第5个周期开端向上添加，这也是由于第5个时钟的实践周期比抱负周期多10ps。
TIE丈量在查验数据流（一般是串行通讯接口）的特性时十分有用，这些传输接口的时钟一般由时钟数据康复（CDR，Clock/Data Recovery ）电路从数据信号中康复出来。比方较大的TIE值或许就说明晰CDR中PLL的响应速度太慢了跟不上数据流的数据改动速率。
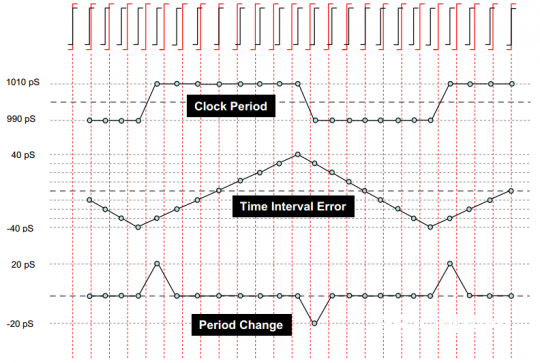
图8 TIE图
4选用实时示波器丈量颤动
4.1示波器设置辅导
丈量时钟颤动最通用的设备当属实时数字示波器，本章将为咱们介绍假如设置示波器以到达更高的丈量精度。
数字示波器选用内部时刻基准来定时采样输入的数据，其采样率可由1Gsps到40Gsps不等。图9列举了数字示波器采样和显现信号的办法。图底部的箭头表明采样点，实线是实践的信号，黑点为采样得到的数据，而示波器显现出的图画（虚线）为依据采样数据通过优化得到的曲线。
或许你会发现采样值与实践信号并不共同，这是由于示波器量化的过程中存在差错。大多数差错是由于示波器为了在规划功能和本钱之间寻求平衡而带来的固有差错，但咱们通过恰当的设置能够缓解为了省钱带来的准确度问题。下面咱们就就来讨论一下形成这些差错的首要原因以及假如通过设置来下降他们对颤动丈量的影响。
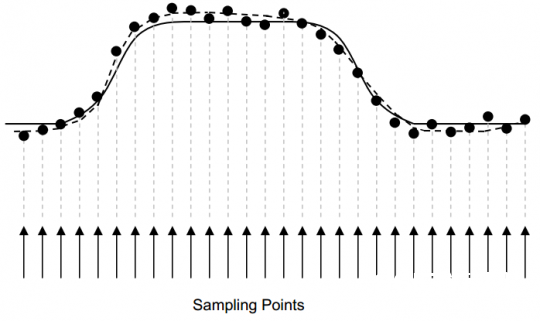
图9数字示波器的采样及显现
4.1.1前端放大器差错
数字示波器的输入信号要通过模仿放大器才干被ADC数字化，而放大器发生的噪声与示波器输入带宽成正比：带宽越宽，噪声越大（兔子：这也是测电源纹波的时分要约束带宽的原因）。可是一位地减小带宽会影响示波器对信号上升和下降时刻的采样，也会引进很大的差错。
这儿有一个通用的描绘信号边缘上升/下降时刻和借款联系的等式：
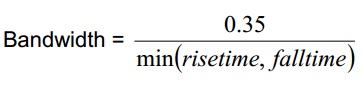*等式5
其间上升时刻或下降时刻丈量方位为信号边缘电平的20%~80%之间。某司引荐将示波器带宽设置为信号带宽的3倍（还有某司出头以为3倍缺乏以复原信号边缘的细节，至少应为5倍），另外在一些示波器中，带宽只能跟着最高采样率的设置改动，乃至有的示波器带宽彻底不能设置。
4.1.2笔直增益引起的量化噪声
量化差错是指采样值与采样点实践信号值之间的不同，这种差错如图9所示。引起这种差错的一部分要素来自于为调整示波器Y轴显现而设置的笔直增益。假如笔直增益过小，示波器或许无法有用运用内部ADC的完好分辨率（许多示波器只要8位的AD）。
某司引荐调整示波器笔直增益直至波形撑满屏幕Y轴。某些示波器中乃至能够将波形调至稍微超出Y轴显现规模，然后运用ADC的额定bit位。不过这一特性取决于你运用的示波器，详细能够咨询厂家。
4.1.3低采样率引起的量化噪声
还有一部分量化噪声是由于示波器横轴方向采样点数缺乏形成的。某司引荐在信号上升/下降沿的20%~80%电平间至少有3个采样点，由此能够推出示波器设置的最低采样率要求。例如，假如信号上升时刻1ns而且需求在这段时刻里确保4个采样点，那么示波器至少要设置4Gsps的采样率。假如你的示波器功能高于这个规范，那么就越大越好啦，设置成最高采样率（实践上除了约束带宽以外，大部分的示波器软件都能依据实践信号主动调理到最佳的横轴和纵轴）。
4.1.4时刻基准颤动
数字示波器采样点的挑选源于内部时刻基准。作为一个时钟源，时刻基准本身存在颤动，而且会添加丈量信号颤动时的差错。一般来说，时基颤动应该小于被测信号颤动期望值的25%，然后到达优于3%的准确度。某司引荐运用你试验室里最好的示波器来进行颤动丈量，由于更高端的设备往往具有更好（更低颤动）的时基电路（好一通废话啊哈哈）。
4.2运用实时示波器丈量颤动的过程
（本节内容根本与2.1-2.3节所述相同，故不做翻译）
4.2.1丈量周期颤动
4.2.2丈量相邻周期颤动
4.2.3丈量长时刻颤动
5定论
本文著成之初有两个意图：其一，向读者描绘今天之高速体系中所能遇见的一般颤动类型；其二，供给借由实时示波器来捕获不同品种颤动的办法过程。兔子翻译此文之意图 已于文前尽言，不复赘述。
