摘要 在信号处理中,滤波的好坏直接影响信息的精确性。仿照滤波尽管方便但不活络,数字滤波效果虽好但杂乱。所以文中提出一种以仿照滤波器为基准,规划具有相同功用并且参数可调的数字滤波器的办法。并以二阶RC无源低通滤波电路为例对此进程进行阐明,与仿照滤波电路和传统的数字滤波比较,该办法不只比传统的数字滤波算法简略方便,并且可有用避免仿照电路中器材的寄生参数、精度、温度等的影响,使滤波愈加安稳。
跟着信息科技的开展,信号处理得到了大幅推进,现已被广泛运用于雷达、通讯、自动化、航空航天等范畴。在信号处理体系中,输入信号一般含有各种噪声和搅扰。为对信号进行精确的丈量和操控,有必要削弱或滤除被测信号中的噪声和搅扰。一般在体系中可选用硬件滤波和软件滤波。硬件滤波又分为无源滤波和有源滤波,无源滤波是经过RC滤波器或LC滤波器等仿照滤波器进行滤波。软件滤波也称数字滤波,是经过必定的算法削弱噪声的影响。硬件滤波的优势是不需要进行杂乱的程序处理,反响活络。而软件滤波的优势是不需要硬件的投入,并且牢靠安稳。
归纳两者的优势,本文提出了一种以低通二阶RC无源滤波电路为基准,用Matlab和Visual C++规划一个具有相同功用数字滤波器的办法即仿照电路数字化办法,以滤除信号中的高频杂波,得到了较为抱负的波形。
1 仿照电路数字化办法
仿照电路数字化的进程如下,首先从硬件滤波电路动身,核算电路的传递函数H(s)。由于软件滤波的信号是离散的数字信号,所以将H(s)转化成离散域的H(z),经过Matlab编程完结对信号的滤波。假如滤波效果不抱负,则对传递函数中的参数进行调整,得到具有较抱负滤波效果的H(z)。为终究用Visual C++编程完结,需要将H(z)反改换得时域的h(t),与信号进行卷积和运算以完结滤波。经过以上进程,完结仿照滤波电路数字化的进程,并在Matlab和Visual C++渠道上完结滤波。
2 二阶RC无源低通滤波电路
关于仿照电路的剖析,一般选用传递函数的剖析办法。电子电路往往是由若干个动态环节连在一起构成一个杂乱电路。关于每个具体环节来说,都有它的输入量和输出量,而必定输入量的改动都会引起输出量的改动。依据一个环节中所进行的物理进程能够写出微分方程,它表明了该环节输出量和输入量的联系。
例如RLC振动回路的微分方程为

输入量与输出量都是时刻t的函数,用微分方程直接表明输入量与输出量时刻函数之间的联系比较杂乱。但运用拉氏改换把时刻函数改换为s的函数今后,原函数关于时刻t的微分积分就简化为s的乘除法。
在零开始条件下,一个动态环节的输出量的拉氏改换用X(s)表明,输入量的拉氏改换用F(s)表明,把
称为传递函数。
一般信号在进行扩大之前,先对该信号进行滤波。以低频信号为例,运用经典的二阶RC无源滤波电路进行滤波,电路如图1所示。在接下来的部分将以此电路为例对仿照电路数字化办法进行具体的剖析和解说。
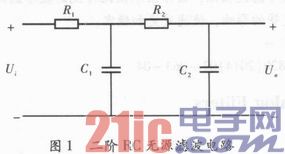
核算出该电路的传递函数H(s)如式(2)所示。其间,b=R1C1+R1C2+R2C2,a=R1R2C1C2。
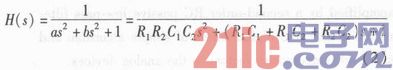
3 传递函数离散化
滤波器的滤波效果与R1、R2、C1和C2等参数相关,假如取值不妥会形成滤波效果不抱负。关于杂乱的传递函数,谐振频率和带宽不易核算,所以本文选用操控变量法。
关于多要素的问题,常常选用操控要素的办法,把多要素的问题变成多个单要素的问题。每一次只改动其间的某一个要素,而操控其他几个要素不变,然后研讨被改动的这个要素对事物的影响,别离加以研讨,最终再归纳处理,这种办法叫操控变量法,被广泛地运用在各种科学研讨之中。
得到传递函数后,就能够对信号进行滤波。由于待处理的数据是数字信号,若想仿真需将频域的传递函数转化为x域的传递函数,行将仿照滤波器转化为数字滤波器。仿照滤波器转化为数字滤波器有两种办法:脉冲呼应不变法和双线性改换法。
脉冲呼应不变法是一个安稳的规划,首要用于规划某些要求在时域上能仿照仿照滤波器功用的数字滤波器。这种改换法的首要特点是频率坐标的改换是线性的,即由于混叠现象,阻带边际的衰减要比仿照滤波器稍差一些,但仍能满意技能指标的要求。脉冲呼应不变法要求该仿照滤波器是带通滤波器或许低通滤波器,但这种办法在阻带没有崎岖的情况下才有用。
双线性改换法映射也是一种安稳的规划,不存在混叠现象,对能够改换的滤波器类型没有约束。但这种办法也有固有缺点:仿照频率和数字频率之间对错线性联系,它使得频率的标度曲折,不能坚持本来的仿照滤波器的相频特性;数字的频率呼应与仿照的频率呼应有显着的不同。一般情况下,能够经过频率的预畸变进行校对。但全体来说,双线性改换法的仿真成果比脉冲呼应不变法愈加抱负。
由于脉冲呼应不变法从s平面到z平面是多值映射,会在频域呼应发生混叠失真。而双线性改换法能够把整个s平面改换到整个z平面上去,且使s的左半平面映射到z平面的单位圆内,所以规划选用双线性改换法。
双线性改动法的映射函数为

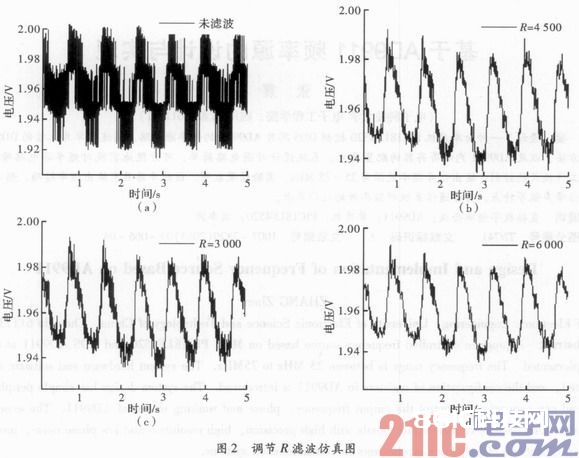
调用Matlab中的Fiher函数R1和R2调理参数、进行仿真,仿真成果如图2所示。图2(a)是未加滤波的波形,图2(b)、图2(c)、图2(d)的电阻顺次增大,从图中能够看到,电阻越大,高频重量越少。
4 时域传递函数
Matlab一般只用于功用仿真,而实践项目运用,一般选用Visual C++软件编程进行信号操控和硬件完结,所以需要将Matlab仿真时运用的滤波器函数Filter转化为C代码完结。
软件编程有时域和频域两种思路。由于输入信号较为杂乱不易进行时-频转化,只能选用时域滤波。所以需将传递函数反改换到时域,对信号进行滤波处理。


5 时域卷积滤波
卷积在通讯技能和信号处理中起着重要的效果。在线性时域体系中,依据时刻的接连性,能够分为卷积积分和卷积和。在LTI接连时刻体系中,把鼓励信号分解为一系列冲激函数,求出各种冲激函数独自效果于体系时的冲激呼应,然后将这些呼应相加就得到体系关于该鼓励信号的零状况呼应。这个相加的进程表现为求卷积积分。在LTI离散体系中,可用上述办法进行剖析。由于离散信号自身是一个序列,因而,鼓励信号分解为单位序列的作业就较简略完结。假如体系的单位序列呼应为已知,那么,也不难求得每个单位序列独自效果于体系的呼应。把这些序列相加就得到体系关于该鼓励信号的零状况呼应,这个相加的进程表现为求卷积和。
由于本体系中的信号是离散时刻序列,常用的卷积和的求解办法有图解法、对位相乘求和法、解析法和列表法等4种。一般,待处理的信号的数据量比较大,列表法不适用,所以选用解析法。
卷积与傅里叶改换有着亲近的联系。运用两个函数的傅里叶改换的乘积等于它们卷积后的傅里叶改换的性质,能使傅里叶剖析中许多问题的处理得到简化。本文正是选用这一点,将频域的滤波转化为时域滤波。
频域相乘等效于时域卷积。编写C程序求输入信号和传递函数的卷积和。当两个信号为因果信号时,能够依据式(5)求卷积和。当f1(k)的数据长度为m;f2(k)的数据长度为n(n
6 成果及剖析
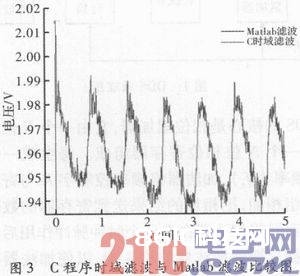
信号别离经卷积和滤波和Filter函数滤波,将滤波后的数据导入Matlab比较,成果如图3所示。由图可见,前者在初始状况呈现尖峰,这是由于卷积和是在特定窗口内时域累加的进程,会形成头部数据和尾部数据不精确。尽管编写的C卷积和滤波程序有必定的缺点,可是全体波形共同,阐明试验取得开始成功。
7 结束语
提出了一种将硬件滤波电路数字化的办法,并在Matlab和Visual C++渠道上得以完结。与仿照滤波电路和传统的数字滤波比较,不只比传统的数字滤波算法简略方便,并且有用避免了仿照电路中器材的寄生参数、精度、温度等的影响,使滤波愈加安稳。