OPENGL坐标系可分为:国际坐标系和当时绘图坐标系。
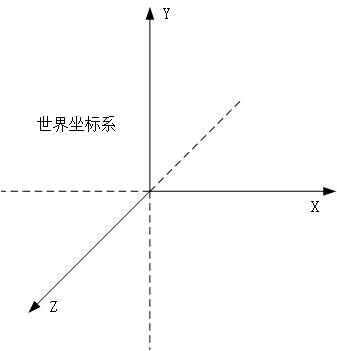
国际坐标系:在OpenGL中,国际坐标系是以屏幕中心为原点(0, 0, 0),且是始终不变的。你面临屏幕,你的右边是x正轴,上面是y正轴,屏幕指向你的为z正轴。长度单位这样来定:窗口规模按此单位恰好是(-1,-1)到(1,1),即屏幕左下角坐标为(-1,-1),右上角坐标为(1,1)。
当时绘图坐标系:是制作物体时的坐标系。程序刚初始化时,国际坐标系和当时绘图坐标系是重合的。当用glTranslatef(),glScalef(), glRotatef()等对当时绘图坐标系进行平移、弹性、旋转改换之后,国际坐标系和当时绘图坐标系不再重合。留意,这儿的平移旋转是将当时绘图坐标系看做一个全体在国际坐标系中进行旋转平移。然后,改动今后,再用glVertex3f()等绘图函数绘图时,都是在当时绘图坐标系进行绘图,一切的函数参数也都是相对当时绘图坐标系来讲的。
齐次坐标
只讲三维的状况啊
向量空间中,只要标量和向量
向量 + 向量 = 向量
标量 * 向量 = 向量
三维向量空间中,能够视恣意一组线性无关的向量为基
基 V = [ v1 , v2 , v3 ]
其他向量能够用一个三维的元组来表明
向量 a = [ A1 , A2 , A3 ]
所以 向量 a = A1 * v2 + A2 * v2 + A3 * v3
仅有向量是无法表明几许的,至少要有点吧
一般以为点的表明也是一个三维的元组
点 b = [ B1 , B2 , B3 ]
这样就无法差异点和向量了,咋办?
仿射空间
仿射空间中,基称为标架,由三个向量和一个点组成
标架 V = [ v1 , v2 , v3 , p ]
仿射空间的运算
向量+ 向量 = 向量
标量 * 向量 = 向量
点 + 向量 = 点
PS:能够看到,点与向量的和为另一个点,其实也能够以为向量记载的是点的运动,记载着一个点转化到另一个点的信息
所以
向量 a = [ a1 , a2 , a3 , 0 ]
点 b = [ b1 , b2 , b3 , 1 ]
即
a = a1 * v1 + a2 * v2 + a3 * v3 , 确实是向量
b = b1 * v1 + b2 * v2 + b3 * v3 + p
b = 向量 + p = 点
牵强差异开了哈
还有问题
点p和向量v1v2v3怎样确认?它们的值又是在那种标架或基下的?
所以评论了再多,这个标架其实仍是对应咱们一般的三维坐标系才显得和蔼可亲,即
点p为原点
v1 v2 v3 别离对应三个坐标轴 [1,0,0]、[0,1,0]、[0,0,1]
只不过我还告知你,关于恣意一个点和恣意三个线性无关的向量v1 v2 v3,其都能够当作一个标架。由于三个线性无关的向量就能够表明出恣意一个向量,再有一个点为根底,就能够表明恣意一个点
所以想OpenGL中就默许,其国际坐标系对应的仿射空间,p为原点,v1v2v3为坐标轴
可是相机坐标系就不是了,由于啥?由于相机能够移动啊,能够改动朝向和正向,这些都影响着相机坐标系。单就移动来说:
相机的默许方位是在国际坐标系的原点,移动了之后就不是了啊
那么你在相机的方位看国际坐标系上的点,那些点的坐标表明就应该转化到相机坐标系上来,才对应着咱们真实应该看到的点的方位
仍是写写坐标系比较真实
坐标系
国际坐标系
国际坐标系的标架

相机坐标系
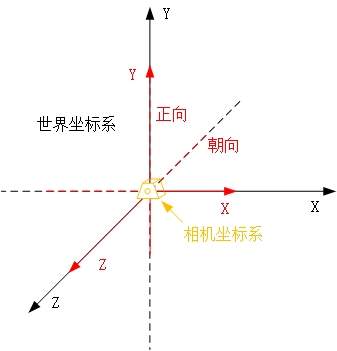
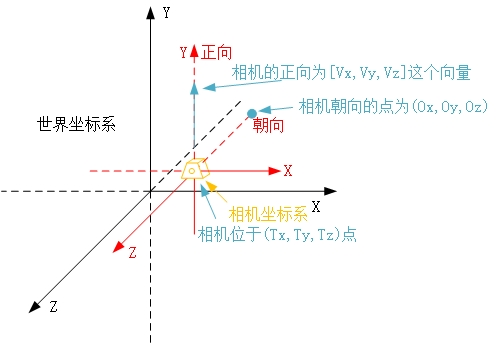
相机默许的方位为国际坐标系原点,朝向是Z轴的负方向,正向是Y轴的正方向
考虑相机
方位便是相机的方位,也便是从哪里去调查这个国际
朝向便是相机对准的方向
正向便是相机该放在这个方位、对准了方向后,该怎样摆。比方一般咱们摄影,竖着摆拍出来的便是竖着的相片,横着摆便是横着的相片。
而这些参数其实也是在国际坐标系下表明的
默许的相机坐标系
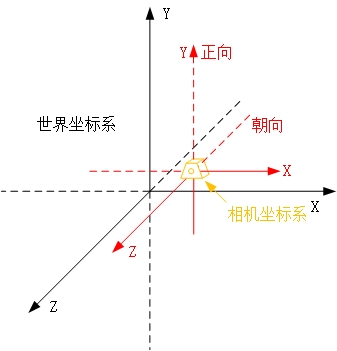
移动相机之后,相机的方位、朝向、正向就改动了
但极点的数据仍是对应着的国际坐标系,而咱们要生成图片是依赖于相机的,所以咱们要把极点转化到相机坐标系下才行,这便是视图的转化。
视图转化后极点的表明便是相关于相机坐标系,但其标架在逻辑上依然是 原点+三个坐标轴
裁剪坐标系
这还仅仅相机的外部参数,咱们还需求确认
那一块的三维区域内的点,我才会拍下来,才会用来生成图画,即我需求规则一块“视景体”来确认摄影的规模
是否需求透视作用等等其他
仍是讲坐标改换比较真实
坐标改换
OpenGL首要有两个矩阵,模型视图矩阵和投影矩阵
模型视图矩阵
对国际坐标系下极点的改动操作,如平移、旋转、缩放(模型)都是对极点的改动,而相机的方位、朝向、正向的改动(视图)也需求极点从相关于国际坐标系下转化到相关于相机坐标系,这两种虽然是不同的改动但都是对极点的操作,所以能够用一个矩阵来记载

便是说只要在原先点的根底上左乘平移矩阵,就能够把点的坐标进行平移改换
记平移矩阵 T 为 T(dx,dy,dz),
旋转
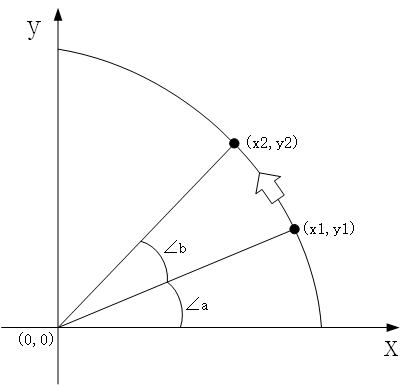
先考虑绕Z轴旋转的状况,正向的旋转为右手大拇指朝向Z轴正向时,其他手指的朝向(逆时针)
绕Z轴旋转至改动X和Y坐标

缩放,便是在原坐标的根底上乘以某个倍数
缩放矩阵
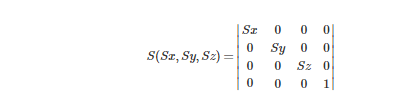
视图矩阵,将以国际坐标系原点为(0,0,0)点的国际坐标系下的极点转化到以相机方位为(0,0,0)的相机坐标系下。
极点和相机之间真实相对方位是不变的,只不过咱们原先极点的坐标表明是在国际坐标系下,而咱们需求的是相机坐标系下的坐标表明。所以这儿仅仅做坐标改换,即同一个极点在不同坐标系下其坐标表明是不同的。
从默许的相机方位能够看到,默许的相机坐标系和国际坐标系是重合的,即不需求转化,其实也便是相当于视图矩阵是单位矩阵罢了
而改动了相机的方位、朝向和正向之后,视图矩阵才会真实的发挥作用,乘上的作用便是让国际坐标系下的极点转化到相机坐标系下
OnenGL经过gluLookAt函数来改动相机的外部参数
gluLookAt( Tx , Ty , Tz , Ox , Oy , Oz , Vx , Vy , Vz )
Tx Ty Tz 为相机的方位
Ox Oy Oz 为相机朝向的点
Vx Vy Vz 为相机的正向
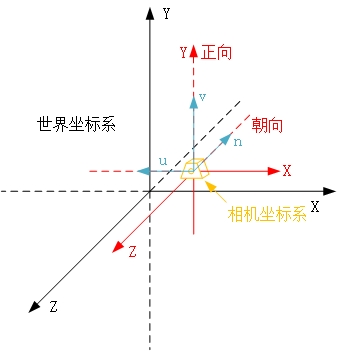
考虑相机的三个向量

n为相机朝向的方向向量
v为相机的正向向量
u为二者叉乘的向量
要求:n和v为相互笔直,nuv三者均为单位向量(只表方向)
那么能够看出这三个向量和相机坐标系的联系
而且咱们还知道相机的方位 Tx Ty Tz
关于极点
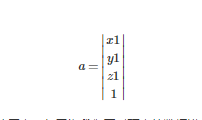
首要咱们把相机移动到国际坐标系的原点,但由于咱们要对极点的数据进行修正,所以就要对极点乘上 T( -Tx , -Ty , -Tz )这样一个平移矩阵。这样以来极点移动到了便是以相机方位为原点的坐标系下
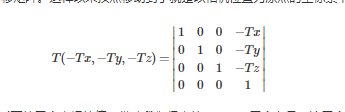
再求这个极点在相机坐标系下的三个坐标的值。凭借咱们得出的 u,v,n三个向量,这三个向量别离对应了相机坐标系的三个坐标轴,所以要求坐标的值也便是看以这个极点为结尾、相机方位为起点的向量和nuv这三个单位向量的点积,相当于乘上这样一个矩阵
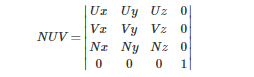
然后咱们得到了坐标的值吗?还没有。由于 向量n和坐标轴z的正向是相反的,向量u和坐标轴x的正向是相反的,所以咱们还需求再乘上一个矩阵来调整
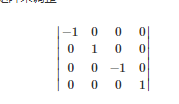
所以咱们终究用来把国际坐标系下的点转化到相机坐标系下的视图矩阵便是

投影矩阵
模型操刁难极点进行改换,其仍是在国际坐标系下
视图操作将极点转化到相机坐标系下
但这二者都是对极点进行改换,所以只需求一个模型-视图矩阵来保护就能够了
那么投影矩阵就需求别的一个内存空间来保护
由于咱们现已把极点转化到了相机坐标系下,所以咱们设置视景体就以相机坐标系来设置
只会glOrtho的矩阵,即正交投影。其视景体是一个方形的区域。
glOrtho( left , right , bottom , top , near , far )
left,right别离对应了x=left和x=right这两个平面
bottom和top别离对应了y=bottom和y=top这两个平面
near和far别离对应了z=-near和z=-far两个平面
这儿取负,首要是由于相机的朝向是z的负方向,这样才会使视景体落在相机的前面
投影矩阵要做的工作,便是一个“标准化”
即依据视景体的规模,对极点进行平移、放缩,使原先在视景体内的点都落在以原点为中心、边长为2的标准化正方体内
这样做的优点便是标准,之后的裁剪、光照等等操作都在一个一致的标准下进行

留意到咱们放缩的时分,关于Z坐标的放缩多了一个负号,这也就意味着一切的点在标准化正方体内是Z坐标的负号是相反的
这也就意味着,咱们要去“看”标准化正方体内的物体的时分,应该从Z轴的负无穷远看向原点,即方向应该是Z的正向
这一步得到的点的坐标,咱们称其坐落裁剪坐标系