怎么使用通讯体系测验中的高斯噪声(上)

噪声产生器是丈量通讯体系功能的有力东西。它答应操作者在参阅信号上参加一个巨细可控的热噪声，然后确认噪声对体系功能(例如比特过错率BER)的影响。热噪声遵从高斯概率密度散布(PDF)，易于从理论剖析走向实践使用。在大都状况下，噪声产生器的输出与实践的(数学意义上的)高斯噪声很挨近，适用于功能剖析和测验使用。本文接下来的部分化说了怎么使用测验中的高斯噪声，以及非抱负的高斯噪声对测验成果有何影响。

体系中信号能量与噪声的比值一般记做E_b/N_o(或是C/N、C/N_o、SNR)，标明信号强度与噪声强度巨细的比率，是衡量通讯信道功能的重要参数。使用加性高斯白噪声核算信噪比的办法现已十分老练，并被广泛地使用于各种首要的通讯规范中(例如MIL-188-165a and ATSC A80)。

白噪声在频谱中所有频率点上的强度都是相同的，是体系功能测验中噪声源的抱负挑选。噪声的概率密度为高斯散布的原因是实践的随机信号都遵从高斯散布，或许说正态散布的。大大都通讯信道中的噪声(如扩大电路引进的噪声)都是热噪声，往往倾向于高斯散布。并且，中心极限定理证明了假如数量足够多的随机事情同时产生，不论单个事情遵守何种散布(均匀散布，高斯散布或其它)，其总和的极限值趋于无穷大并为高斯散布。

高斯散布的数学表达式如下所示：

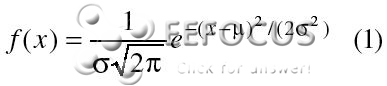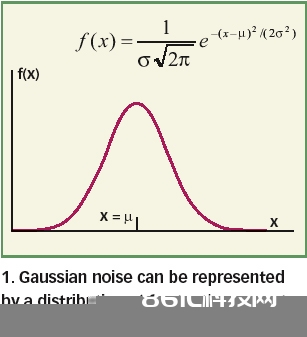
上式给出了一个均值为?，方差为Σ²的变量x的概率散布函数。数学家和计算学家一般称之为正态散布，心理学家称为贝尔曲线，而物理学家和工程师则称为高斯散布。该函数从数学上描绘了高斯噪声的巨细环绕其均值上下动摇的特征(图1)。

使用噪声来丈量体系功能有多种办法，其间一种是在待测信道中参加噪声并不断提高强度，使得信号质量下降直至无法检出停止。举例来说，能够在电视图画中参加“雪花”作为信号噪声。导致信道信号质量下降的噪声强度巨细能够用来评价信号处理技能的才能和功率。

假如需求愈加量化的剖析，有一种办法是把体系容量分为叠加了噪声的信号和没有噪声的信号两部分。没有噪声的信号愈加简略分化(图2)，比方用电压V₀的信号代表数字比特0，电压V₁的信号代表数字比特1。在实践的电子体系中信号上总是存在噪声，这时信号起伏就会环绕V₁ 或V₀上下随机动摇，其概率密度遵守1式给出的高斯散布。

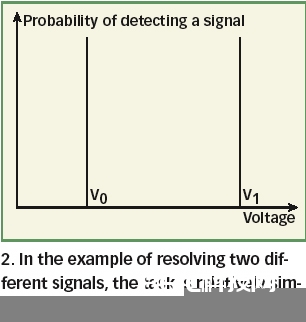假如上述两个信号相隔很远没有相互交迭的话，把他们区别隔不会有什么问题。可是高斯噪声的存在使得信号之间总会有或多或少的交迭(图3)，此刻该怎么区别它们呢？

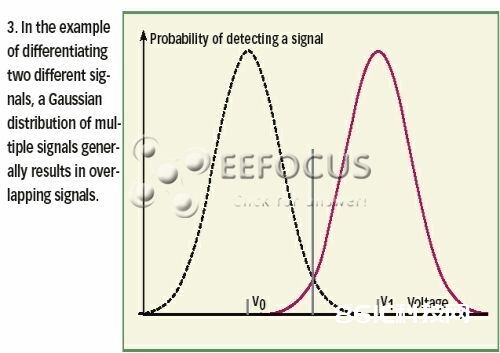解决办法是在二者之间设定一个门限值(V₁–V₀)/2，该值小于V₁大于V₀，假如检测到的信号电压高于该门限则判为1，不然判为0。假如比特0的信号噪声足够大，超出了门限值，会产生什么状况？在判定算法给定的状况下，0会被误判为1，这时就产生了比特误码。

必定数量的过失是无法防止的，因而有必要为比特误码确认丈量规范来衡量问题的严峻程度。核算以下状况呈现的概率是或许的：传送0时因为噪声的存在使得信号电平超越了门限值，或许传送1时噪声与信号相抵使得信号电平降低到门限值以下。依据贝叶斯定理，这个概率能够标明为：

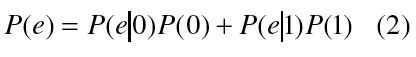上式标明总的过错概率等于0码和1码的过错概率别离乘以它们的呈现概率之和。在一个简略的体系中只要1和0两种信号，且1和0呈现概率大致相同(1和0的呈现或许各占一半)，这时2式能够改写为：

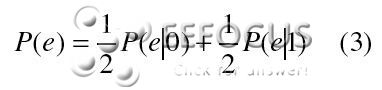0码的过错概率由下式给出：

其间n标明叠加了噪声的信号电压。1码的过错概率为：

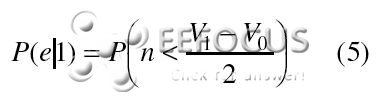因为高斯散布的对称性，高斯噪声信道中依据上两式核算得出的概率数值持平，可统一标明为：

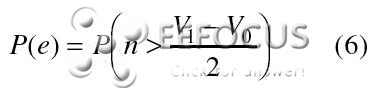上面的比如中体系的比特过错率等于噪声强度超越门限值的概率。高斯散布的计算特性给出了高斯变量x超越给定值a的概率：

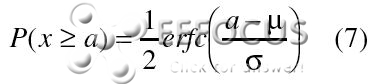其间erfc为互补差错函数，erfc(x)= 1-erf(x)，erf为差错函数。

差错函数erf广泛使用于各种数据剖析的场合，包含解描绘半导体材猜中杂质散布的微分方程。该方程没有解析解，但能够由麦克劳林级数求出近似解。因为其重要性，许多教科书中都列出了erf(x)的数值表，Microsoft Excel乃至把erfc作为其数据剖析东西包Toolpak的一部分。

对应上面的比如，门限值为(V₁– V₀)/2，噪声电压的计算参数为零均值、方差σ²= V_n²，其间V_n²是噪声电压的RMS值。因而7式能够标明为：

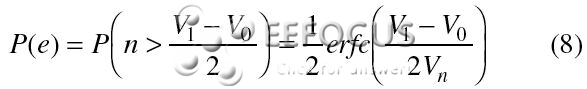为了得出标明功率之比的E_b/N_o表达式，能够把8式变形为以电压的平方来标明：

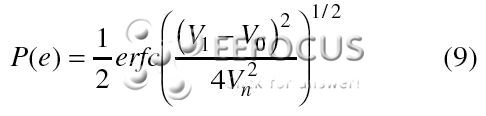上式能够改由功率标明：

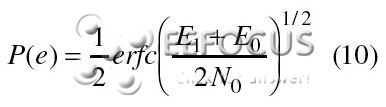其间N_o代表噪声功率密度。因为每比特功率E_b等于两信号功率的均匀，上式还能够改写为：

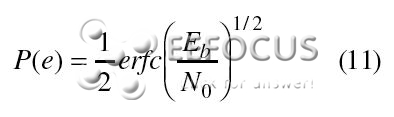至此咱们推导出了二进制移相键控(BPSK)信道中误码率的常用公式。相同的推导办法使用于四进制移相键控(QPSK)和正交QPSK(OQPSK)信道能够得出相同的成果，关于其它调制机制只需把11式稍加变形即可。对这些调制方法的具体的推导超出了本文的规模，可是它很好地解说了该公式(以及使用它得出的“瀑布曲线”)是来源于高斯%&&&&&%的内涵特性。

作者：Peter Matthews