FFT(Fast Fourier Transform,快速傅立叶改换)是离散傅立叶改换的快速算法,也是咱们在数字信号处理技能中经常会提到的一个概念。在大学的理工科课程中,在完结高等数学的课程后,数字信号处理一般会作为通讯电子类专业的专业根底课程进行学习,原因是其间触及了许多的高等数学的理论推导,一起又是各类应用技能的理论根底。
关于傅立叶改换的经典著作和文章十分多,可是看到满篇的杂乱公式推导和罗列,咱们仍是很难从直观上去了解这一杂乱的概念,我想关于一般的测验工程师来说,把握FFT的概念首要应该搞清楚这样几个问题:(1) 为什么需求FFT (2) 改换究竟是怎么进行的 (3) 改换前后信号有何种对应联系(4) 在运用测验东西(示波器或许其它软件渠道)进行FFT的办法和需求留意的问题 (5) 力科示波器与泰克示波器的FFT核算办法的比较
在这篇文章中我尝试用愈加粗浅的解说,尽量不运用公式推导来说一说FFT的那些事儿。
一, 为什么需求FFT?
首要FFT(快速傅立叶改换)是离散傅立叶改换的快速算法,那么提到FFT,
咱们天然要先讲清楚傅立叶改换。先来看看傅立叶改换是从哪里来的?
傅立叶是一位法国数学家和物理学家的姓名,英语原名是Jean Baptiste
Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上宣布了一篇论文,运用正弦曲线来描绘温度散布,论文里有个在其时颇具争议性的出题:任何接连周期信号能够由一组恰当的正弦曲线组合而成。其时检查这个论文的人,其间有两位是历史上闻名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其他检查者投票通过并要宣布这个论文时,拉格朗日坚决对立,在近50年的时刻里,拉格朗日坚持以为傅立叶的办法无法标明带有棱角的信号,如在方波中呈现非接连改动斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的作业,走运的是,傅立叶还有其它工作可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后由于怕被推上断头台而一直在避祸。直到拉格朗日身后15年这个论文才被宣布出来。
谁是对的呢?拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。
可是,咱们能够用正弦曲线来十分迫临地标明它,迫临到两种标明办法不存在能量不同,基于此,傅立叶是对的。
为什么咱们要用正弦曲线来替代本来的曲线呢?如咱们也还能够用方波或三角波来替代,分化信号的办法是无量的,但分化信号的意图是为了愈加简略地处理本来的信号。用正余弦来标明原信号会愈加简略,由于正余弦具有其他信号所不具备的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只要起伏和相位或许发生改动,可是频率和波的形状仍是相同的,且只要正弦曲线才具有这样的性质,正因如此咱们才不必方波或三角波来标明。
傅立叶改换的物理含义在哪里?
傅立叶原理标明:任何接连丈量的时序或信号,都能够标明为不同频率的正弦波信号的无限叠加。而依据该原理创建的傅立叶改换算法运用直接丈量到的原始信号,以累加办法来核算该信号中不同正弦波信号的频率、振幅和相位。当然这是从数学的视点去看傅立叶改换。
那么从物理的视点去看待傅立叶改换,它其实是协助咱们改动传统的时刻域剖析信号的办法转到从频率域剖析问题的思想,下面的一幅立体图形能够协助咱们更好得了解这种视点的转化:
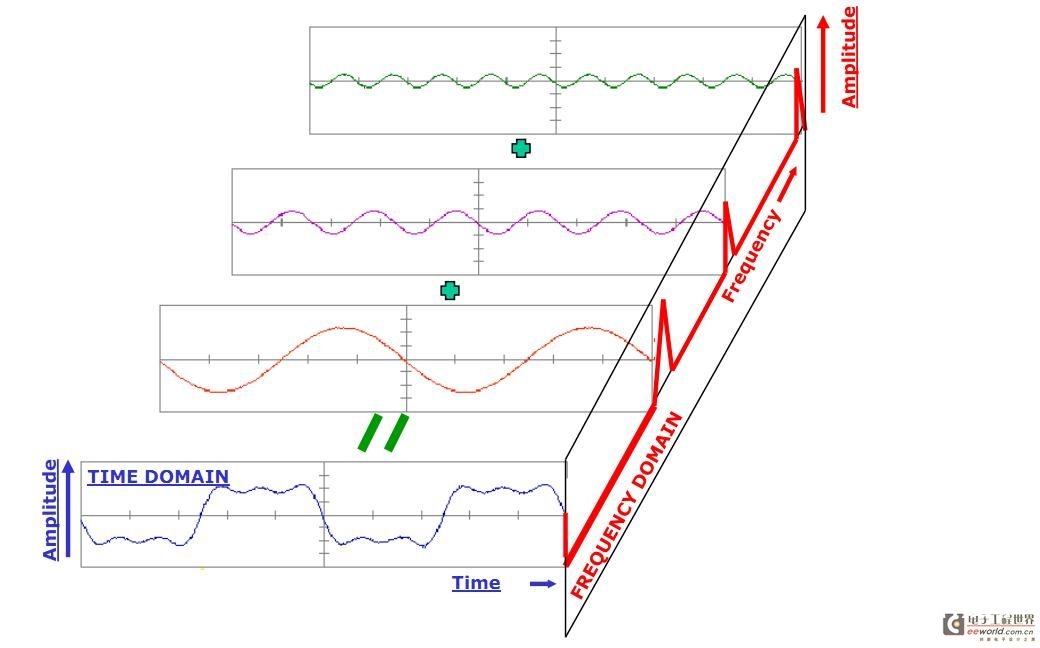
所以,最前面的时域信号在通过傅立叶改换的分化之后,变为了不同正弦波信号的叠加,咱们再去剖析这些正弦波的频率,能够将一个信号改换到频域。有些信号在时域上是很难看出什么特征的,可是假如改换到频域之后,就很简略看出特征了。这便是许多信号剖析选用FFT改换的原因。别的,FFT能够将一个信号的频谱提取出来,这在频谱剖析方面也是经常用的。
傅立叶改换提供给咱们这种换一个视点看问题的东西,看问题的视点不同了,问题或许就便利的解决!
二、 改换是怎么进行的?
首要,依照被改换的输入信号类型不同,傅立叶改换能够分为 4种类型:
1、非周期性接连信号傅立叶改换(Fourier Transform)
2、周期性接连信号傅立叶级数(Fourier Series)
3、非周期性离散信号离散时域傅立叶改换(Discrete Time Fourier Transform)
4、周期性离散信号离散傅立叶改换(Discrete Fourier Transform)
下面是四种原信号图例:
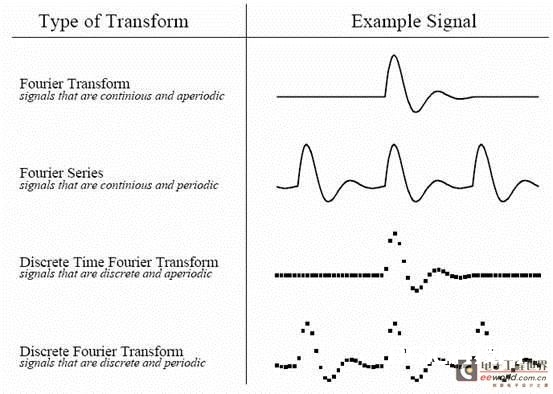
这儿咱们要评论是离散信号,关于接连信号咱们不作评论,由于核算机只能处理离散的数值信号,咱们的终究意图是运用核算机来处理信号的。所以关于离散信号的改换只要离散傅立叶改换(DFT)才干被适用,关于核算机来说只要离散的和有限长度的数据才干被处理,关于其它的改换类型只要在数学演算中才干用到,在核算机面前咱们只能用DFT办法,咱们要评论的FFT也只不过是DFT的一种快速的算法。
DFT的运算进程是这样的:
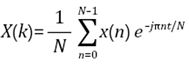
其间,
X(k)—频域值
X(n)—时域采样点
n—时域采样点的序列索引
k—频域值的索引
N—进行转化的采样点数量
可见,在核算机或许示波器上进行的DFT,运用的输入值是数字示波器通过ADC后收集到的采样值,也便是时域的信号值,输入采样点的数量决议了转化的核算规划。改换后的频谱输出包括相同数量的采样点,可是其间有一半的值是冗余的,一般不会显现在频谱中,所以真实有用的信息是N/2+1个点。
FFT的进程大大简化了在核算机中进行DFT的进程,简略来说,假如本来核算DFT的杂乱度是N2次运算(N代表输入采样点的数量),进行FFT的运算杂乱度是Nlg10(N),因而,核算一个1,000采样点的DFT,运用FFT算法只需求核算3,000次,而惯例的DFT算法需求核算1,000,000次!
咱们以一个4个点的DFT改换为例来简略阐明FFT是怎样完成快速算法的:
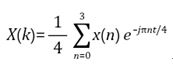
核算得出:
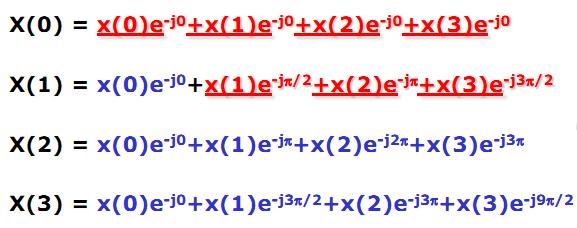
其间的赤色部分在FFT中是有必要核算的重量,其他蓝色部分不需求直接核算,能够由赤色的重量直接推导得到,比方:
x(1)e-j0 = -1*x(1)e-jπ
x(2)e-j0 = x(2)e-j2π
… …
这样,现已核算出的赤色重量只需求核算机将成果保存下来用于之后核算时调用即可,因而大大减少了DFT的核算量。
三、 改换前后信号有何种对应联系?
咱们以一个实践的信号为例来阐明:
示波器采样得到的数字信号,就能够做FFT改换了。N个采样点,通过FFT之后,就能够得到N个点的FFT成果。为了便利进行FFT运算,一般N取2的整数次方。
假定采样频率为Fs,信号频率F,采样点数为N。那么FFT之后成果便是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,便是该频率值下的起伏特性。详细跟原始信号的起伏有什么联系呢?假定原始信号的峰值为A,那么FFT的成果的每个点(除了第一个点直流重量之外)的模值便是A的N/2倍。而第一个点便是直流重量,它的模值便是直流重量的N倍。而每个点的相位呢,便是在该频率下的信号的相位。第一个点标明直流重量(即0Hz),而最终一个点N的再下一个点(实践上这个点是不存在的,这儿是假定的第N+1个点,也能够看做是将第一个点分做两半分,另一半移到最终)则标明采样频率Fs,这中心被N-1个点均匀分红N等份,每个点的频率顺次添加。例如某点n所标明的频率为:Fn=(n-1)*Fs/N。由上面的公式能够看出,Fn所能分辩到频率为为Fs/N,假如采样频率Fs为1024Hz,采样点数为1024点,则能够分辩到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也便是说,采样1秒时刻的信号并做FFT,则成果能够剖析准确到1Hz,假如采样2秒时刻的信号并做FFT,则成果能够剖析准确到0.5Hz。假如要进步频率分辩率,则有必要添加采样点数,也即采样时刻。频率分辩率和采样时刻是倒数联系。
下面这幅图更能够明晰地标明这种对应联系:
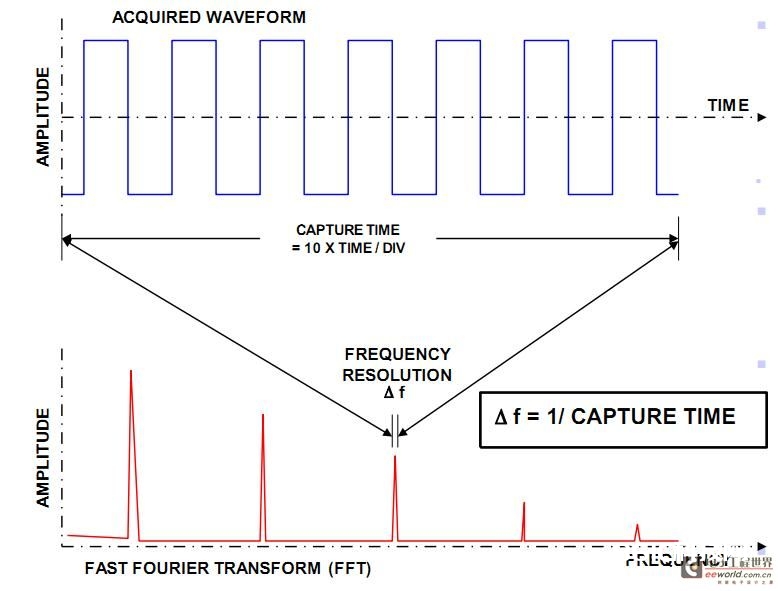
改换之后的频谱的宽度(Frequency Span)与原始信号也存在必定的对应联系。依据Nyquist采样定理,FFT之后的频谱宽度(Frequency Span)最大只能是原始信号采样率的1/2,假如原始信号采样率是4GS/s,那么FFT之后的频宽最多只能是2GHz。时域信号采样周期(Sample Period)的倒数,即采样率(Sample Rate)乘上一个固定的系数便是改换之后频谱的宽度,即 Frequency Span = K*(1/ΔT),其间ΔT为采样周期,K值取决于咱们在进行FFT之前是否对原始信号进行降采样(抽点),由于这样能够下降FFT的运算量。如下图所示: