文章转自ADI官网,版权归属原作者一切
上一篇文章1 评论了滤波器相位与滤波器完成拓扑之间的联系,本篇将评论滤波器传递函数自身的相位漂移。尽管滤波器首要是针对起伏呼应而规划的,但在延时仿真、级联滤波器电路特别是进程操控环路等运用中相位呼应十分重要。
本文首要评论低通和高通呼应。后续系列文章还将评论带通和陷波(带阻)呼应、全通呼应以及滤波器的脉冲与阶跃呼应。
回忆曾经的文章可知,有源滤波器的传递函数能够被看作是滤波器传递函数和放大器传递函数的级联呼应(图1)。

低通传递公式
首要,咱们再看一下传递公式的相位呼应。
关于单极点低通滤波器,传递函数的相移等于:
 |
(1) |
其间ω代表角频率(ω = 2π f 弧度每秒,1 Hz = 2π 弧 度 每 秒),ω0代表滤波器的弧度中心频率。中心频率也可被看作是截止频率。就相位而言,中心频率是相移在整个规模一半处的频率。因为角频率用在比值公式中,因而f/f0彻底能够替代ω/ω0。
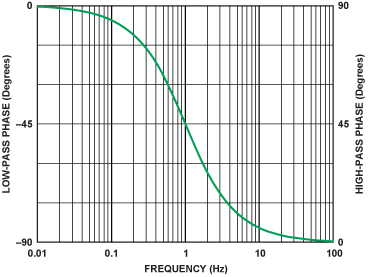
图2(左轴)是在中心频率以下二十倍频到中心频率以上二十倍频规模内对公式1的 求值 成果。因为单 极 点低 通滤 波器 具 有90°的相移规模—从0°至90°—中心频率的相移为-45°。当ω = ω0时,归一化中心频率等于1。

相同,单极点高通滤波器的相位呼应等于
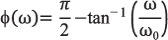 |
(2) |
图2(右轴)是在中心频率以下二十倍频至中心频率以上二十倍频规模内对公式2的求值成果。中心频率 (=1) 的相移等于+45°。
假如低通通带界说为截止频率以下的频率,高通通带界说为中心频率以上的频率,那么最小相移(0°至45°)应在通带内。反之,最大相移(45°至90°)发作在阻带内(频率高于低通截止频率并且低于高通截止频率)。
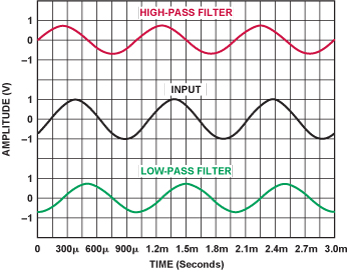
在低通情况下,滤波器输出滞后于输入(负相移);在高通情况下,输出抢先于输入(正相移)。图3显现了相关波形:输入正弦波信号(中心曲线),截止频率为1k H z的单极点高通滤波器输出信号(顶部曲线),截止频率为1k H z的单极点低通滤波器输出信号(底部曲线)。信号频率也是1k H z—两个滤波器的截止频率。图中波形抢先和滞后45°清楚明了。
二阶低通滤波器传递函数的相移能够近似标明为:
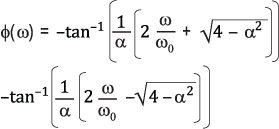 |
(3) |
图4(左轴)是在中心频率以下二十倍频至中心频率以上二十倍频规模内对公式3的求值成果(代入α= √2 = 1.414)。这儿的中心频率等于1,相移为-90°。
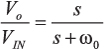
在公式3中,α是滤波器的阻尼比,等于Q的倒数(即Q = 1/α)。它决议了起伏(和瞬态)呼应中的峰值和相位改动的尖利度。α等于1.414很好地表征了双极点巴特沃斯(最大平整度)呼应。
双极点高通滤波器的相位呼应能够被近似标明为:
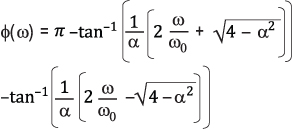 |
(4) |
图4(右轴)是在中心频率以下二十倍频至中心频率以上二十倍频规模内对公式4的求值成果(α=1.414)。在中心频率(=1) 点,相移为90°。
图2和图4只运用了一条曲线,这是因为高通和低通相位呼应是相似的,仅仅相移分别是90°和180°(π/2和π弧度)。这等效于相位符号的改动,导致低通滤波器输出滞后而高通滤波器抢先。
在实践运用中,高通滤波器其实是一个宽带带通滤波器,因为放大器的呼应至少会引进一个低通单极点。
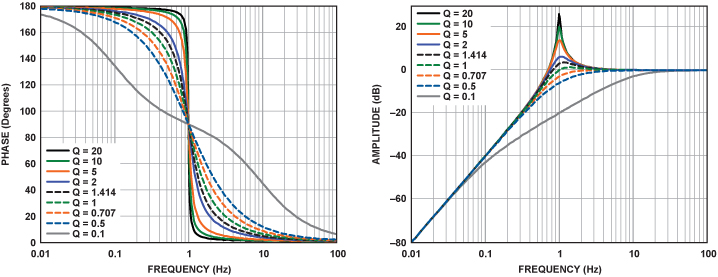
图5是双极点低通滤波器的相位呼应和增益呼应,图中给出了不同Q值时的曲线。这个传递函数标明,相位改动遍及在适当宽规模的频率上,而改动的规模与电路Q值呈反比联系。尽管本文首要评论相位呼应,但相位改动率和起伏改动率之间的联系也值得咱们认真思考。
值得留意的是,每级双极点电路供给最大180°的相移,在极点情况下,相移–180°,尽管滞后360°,但这个视点与180°相移具有相同的特点。根据这个原因,多级滤波器的传递函数图形经常在一个限制规模内,比方180°至–180°,以进步图形读取的准确性(见图9和图11)。在这种情况下,咱们有必要认识到,图形上的视点实践上是真实的视点加上或减去m×360°。尽管在这种情况下图形的顶部和底部会呈现不接连(因为图形改动了±180°),但实践相位视点的改动是滑润和单调的.
图6给出了不同Q值下双极点高通滤波器的增益和相位呼应。这个传递函数标明,180°的相位改动能够发作在很大的频率规模内,而改动的规模反比于电路Q值。别的值得留意的是,曲线的形状十分相似。特别是相位呼应具有相同的形状,仅仅掩盖规模不同。
放大器传递函数
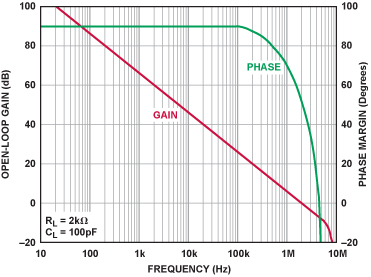
放大器的开环传递函数根本上便是单极点滤波器的传递函数。假如是反相放大器,作用上等同于刺进180°的额定相移。放大器的闭环相移通常被疏忽,但假如它的带宽不行的话,将影响复合滤波器的总传递函数。本文选用了A D822进行滤波器仿真。A D822将影响复合滤波器的传递函数,但仅仅在较高频率处,因为它的增益和相移保持在比滤波器自身的转机频率高得多的频率。从数据手册上摘抄的AD822开环传递函数见图7。
例1:1kHz、5极点、0.5dB切比雪夫低通滤波器
下面举一个1k Hz、5极点、0.5dB的切比雪夫低通滤波器比如进行评论。挑选这个特定比如的原因如下:
1) 与巴特沃斯滤波器不同,切比雪夫滤波器各级电路的中心频率
是彻底不同的,这样能使图形上的曲线扩展得更开一些,使得
图形愈加风趣。
2) 电路的Q值一般要高一点。
3) 奇数个极点能够杰出单极点和双极点电路之间的差异。
滤波器部分选用ADI网站上供给的滤波器规划导游进行规划。
这部分电路的f0和Q见下表:
| f01 = 615.8 Hz | f02 = 960.8 Hz | f03= 342 Hz |
| Q1 = 1.178 | Q2 = 4.545 |
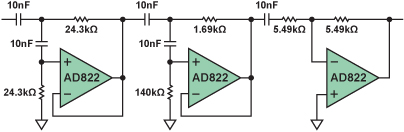
图8是整个滤波器的原理图。所挑选的滤波器拓扑—多反应 (M F B)—又是恣意的,这种挑选使得单极点部分是一个有源积分器,而不是简略缓冲的无源RC电路。
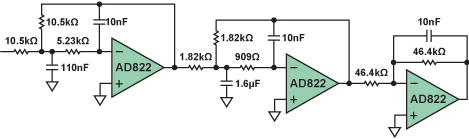
图9给出了整个滤波器的各级电路的相移。图上显现了独自榜首级电路(第1级 — 蓝 色)、前面两级电路(第1和第2级 — 赤色)和整个滤波器(第1、第2和第3级—绿色)的相移。这些相移包含了滤波器部分的根本相移、每个反相放大器奉献的180°相移和放大器频率呼应对总相移的影响。
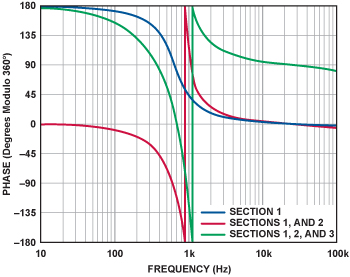
让人感兴趣的一些细节:首要,作为净滞后的相位呼应是负相加的。因为在低频段放大器的倒相,榜首个双极点电路开端相位是–180°(=180°以360°为模),在高频段添加到–360°(=0°以360°为模)。第二级电路添加别的一次倒相,开端相位是–540°(=180°以360°为模),在高频段相位添加到–720°(=0°以360°为模)。第三级电路在低频段的相位开端于–990°(=180°以360°为模),在高频段添加到–990°(=90°以360°为模)。别的需求留意,当频率超越10k H z时,因为放大器的频率呼应,相位将发作轻度的滚降。这种滚降是累积的,每级电路都会有所添加。
例2:1kHz、5极点、0.5dB切比雪夫高通滤波器
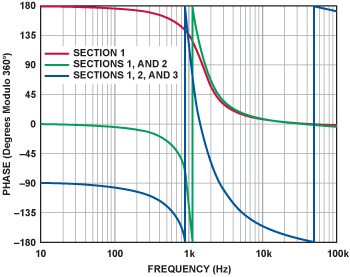
第二个比如(见图10)考虑的是一个1kHz、5极点、0.5dB切比雪夫高通滤波器的相位呼应。在这个比如中,滤波器选用S allen-Key压控电压源(VC V S) 电路而不是多反应 (M F B) 进行规划(仍运用滤波器规划向 导)。尽管是恣意挑选的,但VCVS只需求每级双极点电路两个电容,不像MFB中的每级电路三个电容,并且前两级电路是同相的。

图11给出了滤波器中每级电路的相位呼应。榜首级电路相移开端于低频段的180°,高频段下降到0°。第二级电路在低频段添加了180°,开端于360°(=0°以360°为模),在高频段下降到0°。第三级电路添加了一次倒相,开端于低频段的–180°+90°=-90°,在高频段下降到–540°(= –180°以360°为模)。请再次留意,因为放大器的频率呼应,在高频段会有额定的滚降发作。
结束语
本文评论了低通和高通滤波器的相移特性。这个系列中的前一篇文章介绍了相移与滤波器拓扑之间的联系,在后续文章中,咱们还将评论带通、陷波和全通滤波器—最终,咱们会对一切内容进行回忆,并介绍相移将怎么影响滤波器的瞬态呼应,一起评论群延时、脉冲呼应和阶跃呼应。
附录
单极点和双极点的低通和高通滤波器的通用传递函数见公式A1到公式A4。
单极点低通滤波器的传递函数:
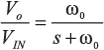 |
(A1) |
其间 s = jω and ω0 = 2πf0.
双极点有源低通滤波器的传递函数:
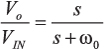 |
(A2) |
其间 HO 是这级电路增益。
单极点高通滤波器的传递函数:
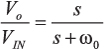 |
(A3) |
双极点有源高通滤波器的传递函数:
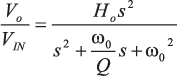 |
(A4) |
1k Hz、0.5dB切比雪夫低通滤波器的f 0和Q值如下:
| 电路 | f0 | Q |
| 第1级 | 690.5 | 1.1779 |
| 第2级 | 1017.8 | 4.5451 |
| 第3级 | 362.3 | —— |
有关更具体的评论请阅览参阅文献6、7和8。
参阅电路
- Zumbahlen, H. “有源滤波器中的相位联系。.” 模仿对话. 第41卷第4期。2007年10月。
- Daryanani, G. 有源网络组成和规划原理. J. Wiley & Sons (1976). ISBN: 0-471-19545-6.
- Graeme, J., G. Tobey and L. Huelsman. 运算放大器的规划和运用。. McGraw-Hill (1971). ISBN: 07-064917-0.
- Van Valkenburg, M.E. 模仿滤波器规划。. Holt, Rinehart & Winston (1982). ISBN: 0-03-059246-1
- Williams, A.B. 电子滤波器规划手册。. McGraw-Hill (1981).
- Zumbahlen, H. “模仿滤波器”第五章Jung, W。运算放大器运用手册。Newnes-Elsevier (2006)。(ADI研讨会笔记的原章节 . 能够在网上找到)。
- Zumbahlen, H. 根本线性规划。 第8章。ADI (2006)。
- Zumbahlen, H. 线性电路规划手册。. Newnes-Elsevier (2008). ISBN: 978-0-7506-8703-4









