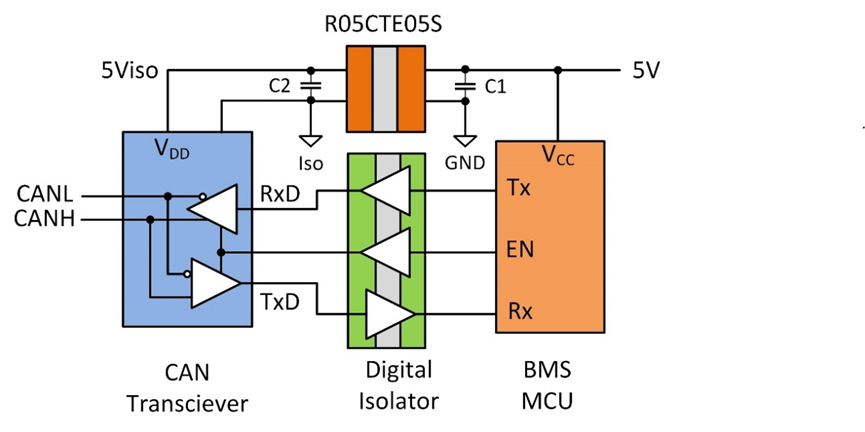
1前语
在发动机的辐射噪声中,结构薄壁件(包含油底壳、气门室罩、正时齿轮室罩等)发生的辐射噪声占总辐射噪声的50%左右,其间油底壳发生的辐射噪声占总量的20%左右[ 1 ] ,因而有必要对该结构进行声学优化,下降发动机的噪声水平。
油底壳一般由薄钢板冲压而成,外表积大而刚度小,跟着曲轴箱的振荡而辐射出很多噪声。许多学者针对油底壳这类薄壁结构进行研究,文献[ 2 ]、文献[ 3 ]经过试验办法对发动机的薄壁件进行了剖析,得出施加结构阻尼资料能够下降薄壁件的辐射噪声;文献[ 4 ]提出在油底壳结构上安置加强板来进步结构刚度然后下降辐射噪声,可是未考虑油底壳中贮存润滑油的状况。因为发动机作业时油底壳中的润滑油与油底壳相互效果会对结构的动态特性及声学特性发生影响[ 5 ] , 运用有限元/鸿沟元法( FEM /BEM)进行剖析时应该考虑这个要素,然后得到准确的成果。关于润滑油的模仿,文献[ 6 ]运用附加质量的办法,该办法能够下降求解核算量和存储空间,但附加质量的确认比较困难。
文中针对某六缸柴油机在标定工况条件下,对油底壳结构选用FEM /BEM直接求解结构的流固耦合方程得到了结构辐射噪声功率级,而且与试验成果进行了比照验证,在此基础上提出两种下降该类薄壁结构辐射噪声的办法,且均具有必定效果。
2有限元流固耦合方程与鸿沟元方程
在油底壳结构中,流体与固体相互效果的部分为流固耦合区,流体的振荡对固体外表发生压力,固体外表的振荡会引起流体的扰动,为流体供给速度或加速度载荷。流固耦合的运动学方程为
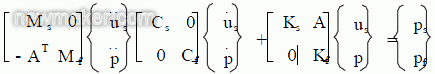
式中Ms、Cs、Ks 为固体结构的质量、阻尼、刚度矩阵;Mf、Cf、Kf 为流体的质量、阻尼、刚度矩阵; A 为流固耦合质量矩阵; us、p分别为固体结构对应节点位移与流体结构对应节点压力; ps、pf 分别为效果在
固体与流体上的载荷。
经过有限元流固耦合方程能够核算得到结构的振荡呼应数据,可是还须对结构振荡对周围外声场发生的辐射噪声特性进行剖析。假定声学体系为线性,将结构的振荡作为声学体系的输入量,声学体系的鸿沟元方程能够描绘为

式中P为声压, ATV (ω)为声响传递向量(Acoustic TransferVector) ,ω为频率, vns (ω)为结构外表法向振荡速度,其间ATV (ω)取决于油底壳的几许形状、润滑油特性、油量及空气的特性阻抗[ 7 ] 。
3模型核算与试验验证
树立油底壳模型及包含润滑油的流固耦合模型如图1。在Nastran中核算油底壳在自在状态下的模态参数,包含模态频率及对应的振型,一起对油底壳结构进行试验模态参数辨认,成果如表1所示,有限元核算模态与试验模态成果符合较好,说明晰有限元模型的正确性,可利用其进行频率呼应核算。
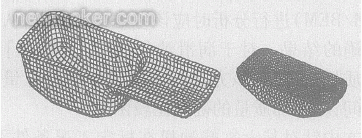
图1 油底壳结构及润滑油有限元模型

因为油底壳为薄壁冲压件,其刚度远小于曲轴箱刚度,且两者之间有密封垫圈的效果,因而模型位移鸿沟条件为将油底壳对应曲轴箱衔接部位沿气缸中心线方向的移动自在度及其它两个方向滚动自在度束缚。