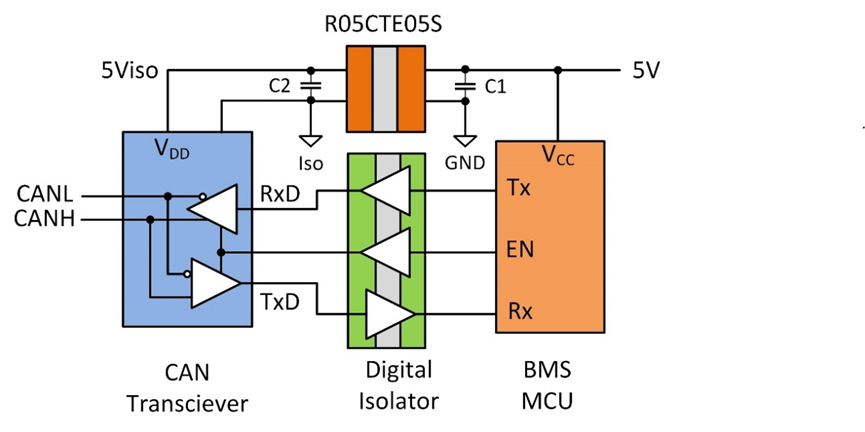
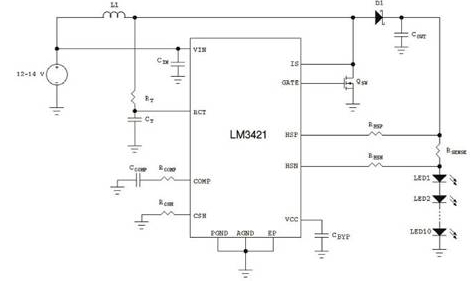
ARM的NEON协处理器技能是一个64/128-bit的混合SIMD架构,用于加快包含视频编码解码、音频解码编码、3D图画、语音和图画等多媒体和信号处理运用。本文首要介绍怎么运用NEON的汇编程序来写SIMD的代码,包含怎么开端NEON的开发,怎么高效的运用NEON。首要会重视内存操作,即怎么改变指令来灵敏有用的加载和存储数据。接下来是由于SIMD指令的运用而导致剩余的若干个单元的处理,然后是用一个矩阵乘法的比如来阐明用NEON来进行SIMD优化,终究重视怎么用NEON来优化各式各样的移位操作,左移或许右移以及双向移位等。本节是一个用NEON优化矩阵乘法的实例。
矩阵
本节将介绍怎么用NEON有用的处理一个4×4的矩阵乘法运算,这种类型的运算常常用于3D图形,咱们以为这些矩阵在内存里是依照列为主摆放的,这是依照OPENGL-ES的通用格局。
矩阵乘法算法
咱们首要看一下矩阵乘法的核算办法,核算的打开,用NEON指令来进行子操作过程。

图1. 以列为主的矩阵乘法运算
由于数据是依照列序存储的,因此矩阵乘法便是把榜首个矩阵的每一列乘以第二个矩阵的每一行,然后把乘积成果相加。乘累加成果 作为成果矩阵的一个元素。
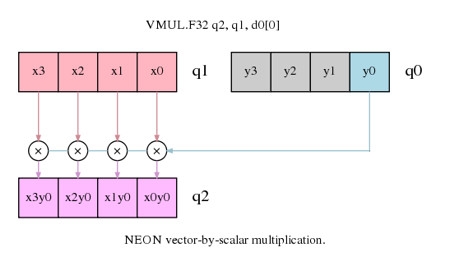
图2. 矩阵乘法中的向量乘以标量的运算
假定每列元素在NEON寄存器中表明为一个向量,那么上述的矩阵乘法便是一个向量乘以标量的运算,而后续的累加也相同可以同向量乘以标量的累加指令完结。由于咱们的操作是在榜首个矩阵的列,然后核算列的成果,读列元素和写列元素都是线性的加载和存储操作,不需求interleave的加载和存储操作。
代码
浮点运算版别
首要看一个单精度浮点的矩阵乘法完结。首要加载矩阵元素到NEON寄存器,然后依照列序做乘法,用VLD1做线性的加载数据到NEON寄存器,用VST1把核算成果保存到内存。
vld1.32 {d16-d19}, [r1]! @ 加载矩阵0的上8个元素
vld1.32 {d20-d23}, [r1]! @ 加载矩阵0的下8个元素
vld1.32 {d0-d3}, [r2]! @ 加载矩阵1的上8个元素
vld1.32 {d4-d7}, [r2]! @ 加载矩阵1的下8个元素
NEON有32个64位寄存器,因此加载一切的输入矩阵元素到16个64-bit寄存器,咱们依然有16个64位寄存器做后续的处理。
D和Q寄存器
大都的NEON指令有两种办法来拜访寄存器组:
- 作为32个双字寄存器,64-bit位宽,命名为d0-d31
- 作为16个四字寄存器,128-bit位宽,命名为q0-q15
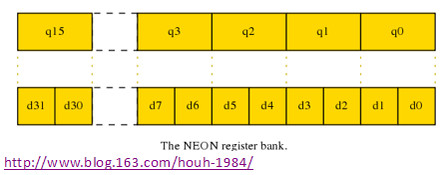
图3. NEON寄存器组
这些寄存器中一个Q寄存器是一对D寄存器的别号,如Q0是d0和d1寄存器对的别号,寄存器中的值可以用两种办法拜访。这种完结办法很相似C言语里的union联合的数据结构。关于浮点的矩阵乘法,咱们会常常运用Q寄存器的表达办法,由于常常会处理4个32-bit的单精度浮点,这对应于128-bit的Q寄存器。
代码部分
经过以下4条NEON乘法指令能完结一列4个成果:
vmul.f32 q12, q8, d0[0] @ 向量乘以标量(MUL),矩阵0的榜首列乘以矩阵1的每列的榜首个元素0
vmla.f32 q12, q9, d0[1] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素1
vmla.f32 q12, q10, d1[0] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素2
vmla.f32 q12, q11, d1[1] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素3
榜首条指令是图2中的列元素x0, x1, x2, x3 (寄存器q8)乘以y0 (d0[0]),然后成果保存到q12寄存器。接下来的指令操作相似,便是把榜首个矩阵的其他列乘以第二个矩阵的榜首列的呼应元素,成果累加到寄存器Q12里。需求留意的是标量元素如d1[1]也可以用q0[3]表明,可是或许编译器如GNU汇编器会不能承受这种办法。
假如咱们只需求矩阵乘以向量的运算,如许多3D图画处理中的那样,那么此刻的核算就完毕了,可以把成果向量保存 到内存了,可是为了完结矩阵相乘,还需求完结后面的迭代操作,运用寄存器Q1到Q3的y4到yF的元素。假如界说如下的宏,那么就能简化代码结构了:
.macro mul_col_f32 res_q, col0_d, col1_d
vmul.f32 \res_q, q8, \col0_d[0] @向量乘以标量(MUL),矩阵0的榜首列乘以矩阵1的每列的榜首个元素0
vmla.f32 \res_q, q9, \col0_d[1] @累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素1
vmla.f32 \res_q, q10, \col1_d[0] @累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素2
vmla.f32 \res_q, q11, \col1_d[1] @累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素3
.endm
那么整个4×4的矩阵乘法代码或许如下:
vld1.32 {d16-d19}, [r1]! @ 加载矩阵0的上8个元素
vld1.32 {d20-d23}, [r1]! @ 加载矩阵0的下8个元素
vld1.32 {d0-d3}, [r2]! @ 加载矩阵1的上8个元素
vld1.32 {d4-d7}, [r2]! @ 加载矩阵1的下8个元素
mul_col_f32 q12, d0, d1 @ 矩阵 0 * 矩阵1的榜首列
mul_col_f32 q13, d2, d3 @ 矩阵 0 * 矩阵1的第二列
mul_col_f32 q14, d4, d5 @ 矩阵 0 * 矩阵1的第三列
mul_col_f32 q15, d6, d7 @ 矩阵 0 * 矩阵1的第四列
vst1.32 {d24-d27}, [r0]! @ 保存成果的上8个元素
vst1.32 {d28-d31}, [r0]! @ 保存成果的下8个元素
定点算法
定点算法核算往往比浮点核算更快,由于往往定点运算或许需求更少的内存带宽,整数值的乘法也会比浮点算法更为简略。可是定点算法,你需求很细心的挑选表明格局来防止溢出或许饱满,这些会影响你的算法终究的精度。定点算法完结的矩阵乘法和浮点算法相似,在本例中,用Q1.14定点格局,可是根本的完结格局根本相似,仅仅完结中或许需求对成果做一些移位调整。下面是列乘的宏:
.macro mul_col_s16 res_d, col_d
vmull.s16 q12, d16, \col_d[0] @ 向量乘以标量(MUL),矩阵0的榜首列乘以矩阵1的每列的榜首个元素0
vmlal.s16 q12, d17, \col_d[1] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素1
vmlal.s16 q12, d18, \col_d[2] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素2
vmlal.s16 q12, d19, \col_d[3] @ 累加的向量乘以标量(MAC),矩阵0的第二列乘以矩阵1的每列的第二个元素3
vqrshrn.s32 \res_d, q12, #14 @ 把成果右移14位,并把累加成果变成Q1.14定点格局,并饱满运算
.endm
比较定点和浮点算法的宏,你会发现如下的首要差异:
- 矩阵元素的值为16位而不是32位,因此用D寄存器来保存4个输入元素
- 矩阵乘法的成果是把16×16=32位的数据,运用VMULL和VMLAL来吧成果保存到Q寄存器。
- 终究成果也是16位,因此需求把32位累加器成果来得到16-bit的成果,运用VQRSHRN,饱满处理把32位的成果舍入到16位的narrow右移操作。
把数据从32-bits变成16-bits也能有用的处理内存拜访,加载和存储数据都只需求更少的带宽。
vld1.16 {d16-d19}, [r1] @ 加载16个元素到矩阵0
vld1.16 {d0-d3}, [r2] @ 加载16个元素到矩阵1
mul_col_s16 d4, d0 @ 矩阵0乘以矩阵1的列0
mul_col_s16 d5, d1 @ 矩阵0乘以矩阵1的列1
mul_col_s16 d6, d2 @ 矩阵0乘以矩阵1的列2
mul_col_s16 d7, d3 @ 矩阵0乘以矩阵1的列3
vst1.16 {d4-d7}, [r0] @ 保存16个成果元素
指令重排
咱们先展现一下指令重排怎么能进步代码功能。在宏中,接近的乘法指令会写入到相同的方针寄存器,这会让NEON的流水线等候前面的乘法成果完结才干开端下一条指令的履行。假如不运用宏界说,而合理组织指令的次第,把那些相关依靠的指令变成不依靠,这些指令就能并发而不会形成流水线的stall。
vmul.f32 q12, q8, d0[0] @ rslt col0 = (mat0 col0) * (mat1 col0 elt0)
vmul.f32 q13, q8, d2[0] @ rslt col1 = (mat0 col0) * (mat1 col1 elt0)
vmul.f32 q14, q8, d4[0] @ rslt col2 = (mat0 col0) * (mat1 col2 elt0)
vmul.f32 q15, q8, d6[0] @ rslt col3 = (mat0 col0) * (mat1 col3 elt0)
vmla.f32 q12, q9, d0[1] @ rslt col0 += (mat0 col1) * (mat1 col0 elt1)
vmla.f32 q13, q9, d2[1] @ rslt col1 += (mat0 col1) * (mat1 col1 elt1)
...
...
用以上的处理办法,矩阵乘法的功能在Cortex-A8处理平台上功能提高了一倍。从文档arm.com/help/index.jsp?topic=/com.arm.doc.set.cortexa/index.html” rel=”nofollow”>Technical Reference Manual for your Cortex core可以看到 各个指令的需求时刻以及推迟,有这些推迟周期,可以更为合理的组织代码次第,提高功能。