滤波是信号处理中的一个重要概念。滤波分经典滤波和现代滤波。
经典滤波的概念,是依据富立叶剖析和改换提出的一个工程概念。依据高等数学理论,任何一个满意必定条件的信号,都能够被看成是由无限个正弦波叠加而成。换句话说,便是工程信号是不同频率的正弦波线性叠加而成的,组成信号的不同频率的正弦波叫做信号的频率成分或叫做谐波成分。只答应必定频率规模内的信号成分正常经过,而阻挠另一部分频率成分经过的电路,叫做经典滤波器或滤波电路。
实践上,任何一个电子体系都具有自己的频带宽度(对信号最高频率的约束),频率特性反映出了电子体系的这个根本特色。而滤波器,则是依据电路参数对电路频带宽度的影响而规划出来的工程运用电路。
用模仿电子电路对模仿信号进行滤波,其根本原理便是运用电路的频率特性完成对信号中频率成分的挑选。依据频率滤波时,是把信号看成是由不同频率正弦波叠加而成的模仿信号,经过挑选不同的频率成分来完成信号滤波。
当答应信号中较高频率的成分经过滤波器时,这种滤波器叫做高通滤波器。
当答应信号中较低频率的成分经过滤波器时,这种滤波器叫做低通滤波器。
当只答应信号中某个频率规模内的成分经过滤波器时,这种滤波器叫做带通滤波器。
抱负滤波器的行为特性一般用起伏-频率特性图描绘,也叫做滤波器电路的幅频特性。抱负滤波器的幅频特性如图所示。图中,w1和w2叫做滤波器的截止频率。

滤波器频率响应特性的幅频特性图
关于滤波器,增益起伏不为零的频率规模叫做通频带,简称通带,增益起伏为零的频率规模叫做阻带。例如关于LP,从-w1当w1之间,叫做LP的通带,其他频率部分叫做阻带。通带所表明的是能够经过滤波器而不会发生衰减的信号频率成分,阻带所表明的是被滤波器衰减掉的信号频率成分。通带内信号所取得的增益,叫做通带增益,阻带中信号所得到的衰减,叫做阻带衰减。在工程实践中,一般运用dB作为滤波器的起伏增益单位。
低通滤波器
低通滤波器的根本电路特色是,只答应低于截止频率的信号经过。
(1)一阶低通Butterworth滤波电路
下图a和b是用运算扩大器规划的两种一阶Butterworth滤波电路的电路。图a是反相输入一阶低通滤波器,实践上便是一个积分电路,其剖析办法与一阶积分电路相同。
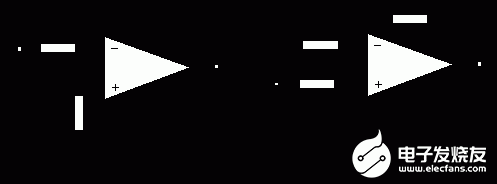
根本滤波电路 演示
图b是同相输入的一阶低通滤波器。依据给定的电路图能够得到

对滤波器来说,更关怀的是正弦稳态是的行为特性,运用拉氏改换与富氏改换的联系,有

下图是上式RC=2时的幅频特性和相频特性波特图。
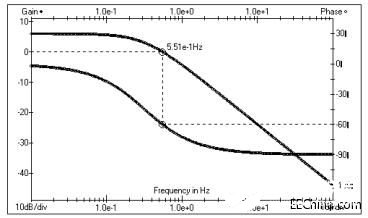
RC=2时一阶Butterworth低通滤波器的频率响应特性
(2)二阶低通Butterworth滤波电路
下 图是用运算扩大器规划的二阶低通Butterworth滤波电路。

二阶Butterworth低通滤波电路
直接选用频域剖析办法得到
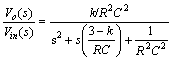
其间k = 1+R1/R2 。令Q=1/(3-k),w0=1/RC,则能够写成
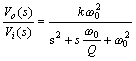
其间k相当于同相扩大器的电压扩大倍数,叫做滤波器的通带增益,Q叫做品质因数,w0叫做特征角频率。
下图是二阶低通滤波器在RC=2时的波特图,其间图a是Q》0.707时的作用,图b是Q=0.707时的作用,图c是Q《0.707时的作用。

(a) Q》0.707

(b) Q=0.707

(c)Q《0.707
二阶低通滤波器在RC=2时的波特图
从图中能够看出,当Q》0.707 或Q《0.707时,通带边缘处会呈现比较大的不平坦现象。因而,品质因数表明晰滤波器通带的状况。一般要求Q=0.707。
由此能够得到
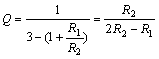
这便是二阶Butterworth滤波器电压增益得核算0.707公式。令Q=0.707,得
0.414R2 = 0.707R1
一般把最大增益倍所对应的信号频率叫做截止频率,这时滤波器具有3dB的衰减。运用滤波器幅频特性的概念,能够得到截止频率w0 =w =1/RC,即
f =1/2pRC

高通滤波器的特色是,只答应高于截止频率的信号经过。下图是二阶Butterworth高通滤波器电路的抱负物理模型。
直接选用频域剖析办法,并令k = 1+R1/R2 ,Q =1/(3-k),w0=1/RC,则能够得到二阶Butterworth高通滤波电路的传递函数为
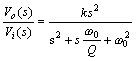
二阶Butterworth高通滤波电路 演示
高通滤波器
考虑正弦稳态条件下,s=jw,得

二阶BButterworth高通滤波器在频率响应特性与低通滤波器类似,当Q》0.707或Q《0.707时,通带边缘处会呈现不平坦现象。有关依据品质因数Q核算电路电阻参数R1 和R2的办法与二阶低通滤波器的核算相同。
相同,运用滤波器幅频特性的概念,能够得到截止频率w0 =w =1/RC,即 f =1/2pRC
责任编辑:gt