0 导言
现在根据传感器的温度补偿办法首要分为模仿硬件规划和数字信号处理两种办法。模仿硬件一般选用PTAT 和CTAT 等技能来规划读出电路。数字信号处理办法一般包含线性拟合、最小二乘多项式 拟合、BP神经网络 、卡尔曼滤波 、支撑向量机等算法。本文在这些算法的基础上提出一种双指数函数模型的温度补偿算法,有以下长处:
(1)指数函数具有无限阶的泰勒展开式,因而双指数函数在比照如传感器温度系数曲线这类非线性曲线的拟合上能够到达很高的精度。
(2)本文提出一种具有高精度初值的替换迭代法 ,即别离系数法。首要选用4组数据点,联立方程组,求出非线性系数的初始值,其次运用替换迭代法核算得到优化后的线性和非线性系数。整个算法处理了直接运用替换迭代法核算发生的迭代不收敛、精度较低、迭代次数较多的问题。
(3)在传感器温度补偿中,因为双指数函数系数只要4个,能够运用CORDIC算法规划硬件补偿电路来集成到传感器中,其间系数保存在ROM中即可,因而具有很好的工程实用价值。
1 替换迭代法拟合双指数函数
根据传感器温度补偿的双指数函数模型为式(1)。


(5)重复过程(2)、(3)和(4),使线性系数和非线性系数核算替换进行,直到均方差错Δ满意给定的规模停止。
替换迭代法仅运用非线性系数作为初值,在必定程度下降低了初值选取难度,不过对非线性系数仍然有依赖性,因而在拟合过程中,非线性系数初值的选取就起到了至关重要的作用。
2 别离系数法核算非线性系数初值
本节选用别离系数法[9]来核算非线性初值。详细算法如下:
(1)在数据点中挑选4组数据点{(Vtempi,Vouti)},i=1,2,3,4。其间Vtemp1《Vtemp2《Vtemp3《Vtemp4,且VouTI同号。
(2)将点1和点2带入双指数函数式(1)中得到式(4)和式(5):
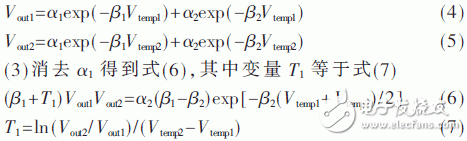
(4)将点2和点3带入式(1)能够得到与式(6)相似的方程,二者联立能够消去线性参数α2,得到式(8),其间T2由式(7)下标加1得到。
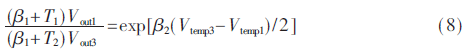
(5)将式(8)两头取对数再近似带入中点微分消除对数可得式(9),其间中心变量A1、B1、C1、D1表达式由式(10)所示:
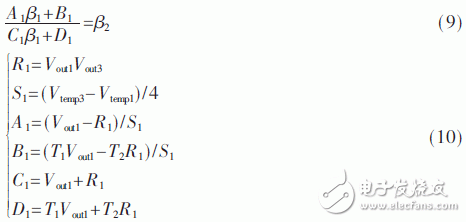
(6)再运用点2、3、4还能够导出相似于式(9)的方程,如式(11)。其间系数为式(10)下标加1即可。

(7)联立式(9)和式(11),消去一个非线性系数β2,求解一个一元二次方程组得到另一个非线性系数β1的两个解,再由式(9)求得β2。
别离系数法选用数据点对系数别离,终究将逾越函数方程转换为一元二次方程求解。选用该办法时能够屡次测验不同的4点来比照拟合成果。一般来说,观测点相对密布和均匀时,差错相对较小。得到精度较高的非线性系数初始值后,将核算得到的初始值,运用第一节介绍的替换迭代法核算线性系数并优化成果,能够得到拟合精度较高的双指数函数方程,为温度补偿供给较为精准函数模型。
3 仿真试验与剖析
3.1 双指数函数拟合
对两组数据(x1,y1)和(x2,y2)进行试验测验,详细数据见表1。
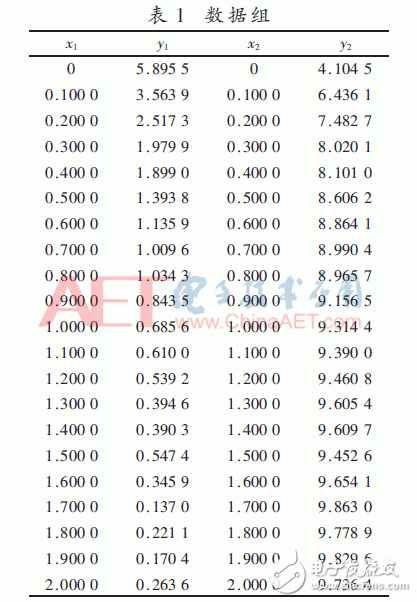
选用matlabR2013软件对数据(x1,y1)和(x2,y2)进行拟合。拟合成果如图1、图2所示。图1(a)和图2(a)选用本文提出的算法,首要算出高精度的非线性系数初始值,分别为β1=17.614 6、β2=1.314 7和β1=-0.092 9、β2=7.568 5,图1和图2(b)、图2(c)选用不同的线性初始值进行比照。表2和表3分别为对图1和图2三种拟合作用进行定量剖析,运用均方根差错(RMSE)和确认系数(R_square)作为点评目标。
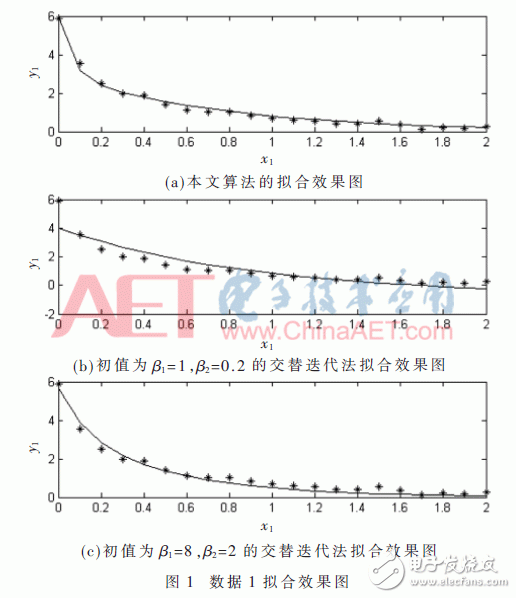


从表中成果能够看出,本文提出的算法,提高了初始值准确性,降低了均方差错,提高了确认系数,有较好的拟合作用。
3.2 根据传感器温度补偿
在本末节中,为了验证本文的算法和模型在传感器温度补偿中的有效性,运用一款MEMS加速度计,在温箱中进行零位温度循环试验。将收集到的数据进行预处理,详细过程如下:
(1)试验数据导入MATLAB中进行数据理,取温度循环试验中的全温试验一段即Vtemp从0.4 V~0.67 V(实践温度相当于-40 ℃~60 ℃)。
(2)将数据进行小波降噪和除掉奇特值。
(3)选用移动均匀法进行滑润处理并等间隔得采样50个数据点作为待拟合的数据。成果如图3(a)、图3(b)、图3(c)、图3(d)所示。
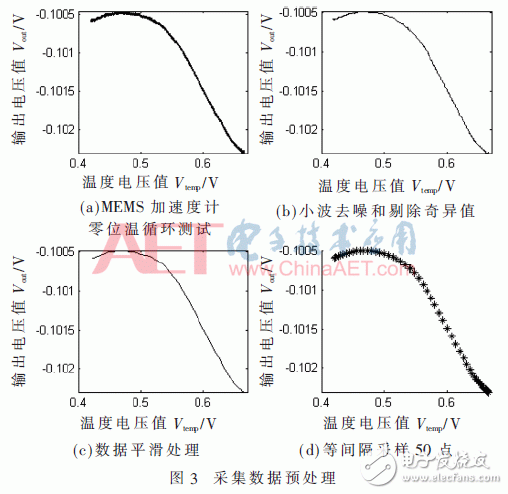
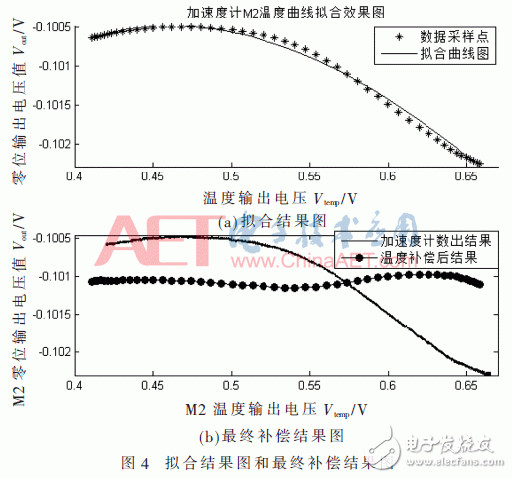
图4(a)、图4(b)为拟合成果图和终究补偿成果图。拟合成果RMSE=4.874 2&TImes;10-5,R_square=0.994 3。将MEMS加速度计原始输出进行补偿后,最大差错(峰峰值)从1.851 3&TImes;10-5下降到1.735 0&TImes;10-5。减少了一个数量级。
4 结束语
本文在现有温度补偿算法的基础上,首要提出了一种双指数函数模型的温度补偿办法。其次,在考虑到传统的替换迭代法进行双指数函数拟合过程中因为初值选取不妥导致的迭代不收敛、精度较低、迭代次数较多的问题时,提出一种别离系数法 ,该办法能够有效地核算出高精度的初值,然后得到高精度的拟合成果。终究将算法应用到传感器温度补偿中,补偿成果表明温度系数曲线最大差错降低了一个数量级。具有必定实用价值。下一步能够选用CORDIC算法将双指数函数模型硬件完成,系数储存在ROM中,规划一款数字补偿电路集成到传感器芯片中,只需要改动4个系数,替代单片机,完成自动化的温度补偿。