Cyclic Redundancy Check循环冗余查验,是依据数据核算一组效验码,用于核对数据传输过程中是否被更改或传输过错。
算法原理
假定数据传输过程中需求发送15位的二进制信息g=101001110100001,这串二进制码可表明为代数多项式g(x) = x^14 + x^12 + x^9 + x^8 + x^7 + x^5 + 1,其间g中第k位的值,对应g(x)中x^k的系数。将g(x)乘以x^m,既将g后加m个0,然后除以m阶多项式h(x),得到的(m-1)阶余项r(x)对应的二进制码r便是CRC编码。
h(x)能够自由挑选或许运用世界通行规范,一般依照h(x)的阶数m,将CRC算法称为CRC-m,比方CRC-32、CRC-64等。
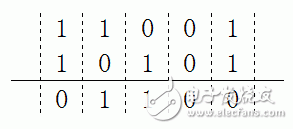
g(x)和h(x)的除运算,能够经过g和h做xor(异或)运算。比方将11001与10101做xor运算:
理解了xor运算规则后,举一个比方运用CRC-8算法求101001110100001的效验码。CRC-8规范的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1,既h是9位的二进制串111010101。

经过迭代运算后,终究得到的r是10001100,这便是CRC效验码。
经过示例,能够发现一些规则,依据这些规则调整算法:
1. 每次迭代,依据gk的首位决议b,b是与gk进行运算的二进制码。若gk的首位是1,则b=h;若gk的首位是0,则b=0,或许越过此次迭代,上面的比方中便是碰到0后直接跳到后边的非零位。

2. 每次迭代,gk的首位将会被移出,所以只需考虑第2位后核算即可。这样就能够放弃h的首位,将b取h的后m位。比方CRC-8的h是111010101,b只需是11010101。
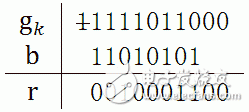
3. 每次迭代,受到影响的是gk的前m位,所以构建一个m位的寄存器S,此寄存器贮存gk的前m位。每次迭代核算前先将S的首位扔掉,将寄存器左移一位,一起将g的后一位参加寄存器。若运用此种办法,核算过程如下:
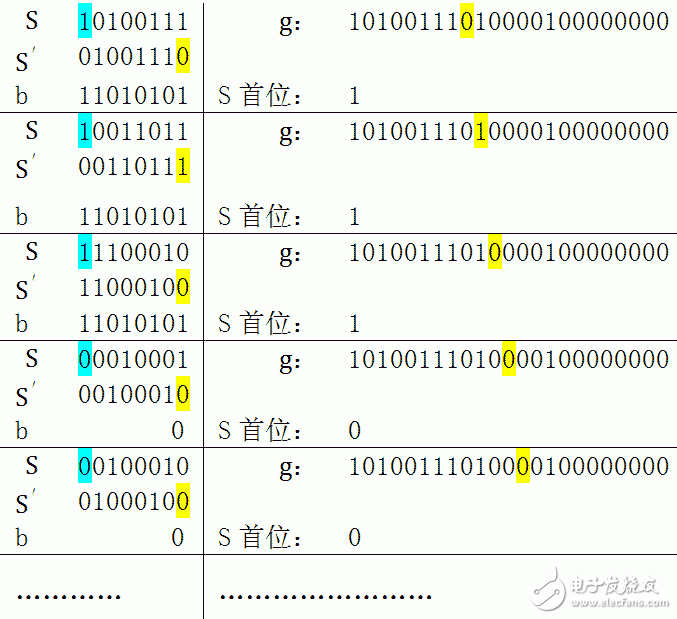
※蓝色表明寄存器S的首位,是需求移出的,b依据S的首位挑选0或许h。黄色是需求移入寄存器的位。S‘是经过位移后的S。
查表法
同样是上面的那个比方,将数据按每4位组成1个block,这样g就被分红6个block。

下面的表展现了4次迭代核算过程,灰色布景的位是保存在寄存器中的。
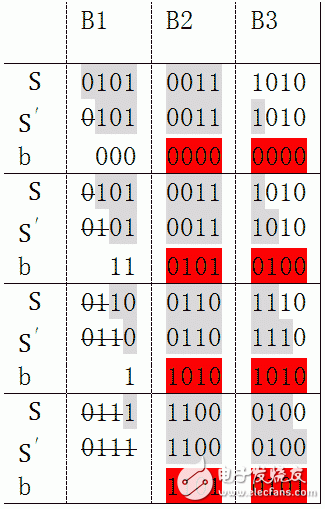
经4次迭代,B1被移出寄存器。被移出的部分,不咱们关怀的,咱们关怀的是这4次迭代对B2和B3产生了什么影响。注意表中赤色的部分,先作如下界说:
B23 = 00111010
b1 = 00000000
b2 = 01010100
b3 = 10101010
b4 = 11010101
b’ = b1 xor b2 xor b3 xor b4
4次迭代对B2和B3来说,实践上便是让它们与b1,b2,b3,b4做了xor核算,既:
B23 xor b1 xor b2 xor b3 xor b4
能够证明xor运算满意交换律和结合律,所以:
B23 xor b1 xor b2 xor b3 xor b4 = B23 xor (b1 xor b2 xor b3 xor b4) = B23 xor b‘
b1是由B1的第1位决议的,b2是由B1迭代1次后的第2位决议(既是由B1的第1和第2位决议),同理,b3和b4都是由B1决议。经过B1就能够核算出b’。别的,B1由4位组成,其总共2^4有种或许值。所以咱们就能够想到一种更方便的算法,事前将b‘一切或许的值,16个值能够当作一个表;这样就能够不用进行那4次迭代,而是用B1查表得到b’值,将B1移出,B3移入,与b‘核算,然后是下一次迭代。

可看到每次迭代,寄存器中的数据以4位为单位移入和移出,关键是经过寄存器前4位查表取得
,这样的算法能够大大提高运算速度。
上面的办法是半字节查表法,别的还有单字节和双字节查表法,原理都是相同的——事前核算出2^8或2^16个b’的或许值,迭代中运用寄存器前8位或16位查表取得b‘。
反向算法
之前评论的算法能够称为正向CRC算法,意思是将g左面的位看作是高位,右边的位看作低位。G的右边加m个0,然后迭代核算是从高位开端,逐渐将低位参加到寄存器中。在实践的数据传送过程中,是一边接纳数据,一边核算CRC码,正向算法将新接纳的数据看作低位。
逆向算法望文生义便是将左面的数据看作低位,右边的数据看作高位。这样的话需求在g的左面加m个0,h也要逆向,例如正向CRC-16算法h=0x4c11db8,逆向CRC-16算法h=0xedb88320。b的挑选0仍是h,由寄存器中右边第1位决议,而不是左面第1位。寄存器仍旧是向左位移,便是说迭代变成从低位到高位。