0 导言
SPWM技能现在已经在实践中得到十分遍及的运用[1]。经过长时间的开展,大致可分红电压SPWM,电流SPWM 和磁通SPWM,其间电压和电流SPWM 是从电源视点动身的SPWM,而电压空间矢量PWM则是从电动机视点动身的SPWM[2]。本文将介绍单相采样型电压SPWM波的生成和三相采样型电压SPWM波的生成办法。
1 单相SPWM波的生成
对称规矩采样的数学模型十分简略,可是因为每个载波周期只采样一次,因而所构成的阶梯波与正弦的迫临程度仍存在较大的差错[3]。假如既在三角波的极点对称轴方位采样,又在三角波的底点对称轴方位采样,也便是每个载波周期采样两次,这样所构成的阶梯波与正弦波的迫临程度会大大提高。不对称规矩采样法生成的SPWM 波如图1所示。称其为不对称规矩采样法。
由图1 可得,当在三角波的极点对称轴方位t1时间采样时,则有

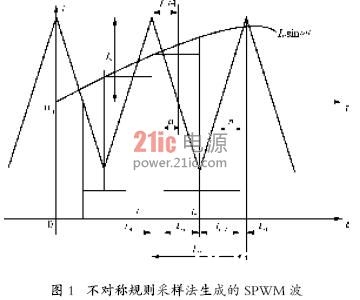
当在三角波的底点对称轴方位t2时间采样时,则有

将三角形类似关系式(3)代入式(1)和式(2),得


不对称规矩采样法的数学模型虽然稍微杂乱一些,但因为阶梯波更接近于正弦波,所以谐波重量的幅值更小,在实践中得到更多的运用[4]。以上是单相SPWM波生成的数学模型。
2 三相SPWM 波的生成
如要生成三相SPWM波,有必要运用三条正弦波和同一条三角波求交点。三条正弦波相位差是2仔/3,即


3 结语
应当指出的是,优化后的SPWM波形并不意味着消除或减少了总的谐波能量,而仅仅改变了各次谐波的组成,因为低次谐波不易由滤波电路消除且对机电设备及外部线路形成的影响高于高次谐波,因而一般进行优化SPWM时,原则上都是尽量削弱低次谐波而由高次谐波承当总的谐波能量,再经过滤波电路将易于完成滤波的高次谐波消除。