arm芯片的浮点运算

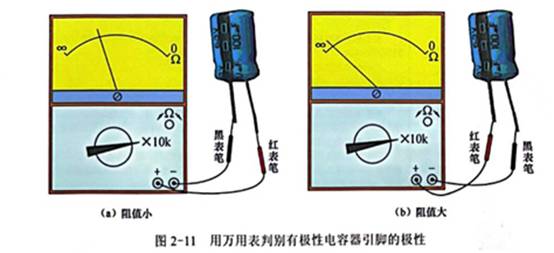
微软MSDN上关于ARM芯片浮点运算的材料
勿运用浮点运算
ARM 处理器并不支撑浮点运算 (Floating Point Math)。一切的浮点运算都是在浮点运算模拟器上进行，因而特别缓慢。需求浮点运算的函式，常要消耗数千个循环才干履行结束。这便是为何游戏开发时，一般都运用定点 (Fixed Point) 格局的运算。定点运算实际上是运用整数，但指定固定数目的位元做為数值的分数部份。就好像是指定某一数字，其千位数以下為分数。若要表明 0.500，只需乘以 1000，便得到 500 这个数值。
比较困难的部份，是开发人员有必要随时想像这个隐形的小数点。加法与减法比较没有问题：
500 + 500 = 1000 (可视為：0.500 + 0.500 = 1.000)。
乘法与除规律较為困难：
500 * 500 = 250000 (但若视為：0.500 * 0.500 = 250.000) 成果会不正确。
两个定点数值相乘后，有必要以除法调整有效位数。若将成果除以 1000，则得到正确值 (250.000/ 1000 = 0.250 為正确的成果)。因而，进行乘法运算时，先做一般的乘法运算，再以除法调整成果的有效位数。
上述方法会引出一项风趣的问题。相乘后但没有调整位数前，此居中数值的规模為何？
在上例中，履行乘法后，数值或许会超越答应的位元数。亦即或许会形成溢位，而得不到您想要的成果。解决方法是為居中数值指定适宜的材料格局，保证能贮存或许的最大值。当您将两个 32 位元数值相乘时，居中数值有必要是 64 位元。调整位数后 (以及切断数值)，成果会恢復為 32 位元。
int Multiply16_16_by_16_16( int a16_16, int b16_16 )
{
__int64 tmp32_32;
int result16_16;
tmp32_32 = a16_16;
tmp32_32 *= b16_16; // 现在成果為 32:32
tmp32_32 >>= 16; // 切断 16 个低位元
result16_16 = ( int ) tmp32_32; // 切断 16 个高位元
// 现在成果回到 16:16
return result16_16;
}
若要除法运算，则履行相反的程序：先以乘法调整，再进行相除。
常用的定点格局為 16:16，亦即前 16 位元代表整数部份，后 16 位元代表分数部份。 以此游戏专案而言，运用了各种不同的格局，以便应用在游戏引擎中各种规模的数值。简而言之，共运用了 2:30、8:24、16:16、24:8、28:4、2:14、8:8、11:5、2:8 以及4:4。其间大多数是 32 位元数值，但有些是 16 位元、10 位元或 8 位元。