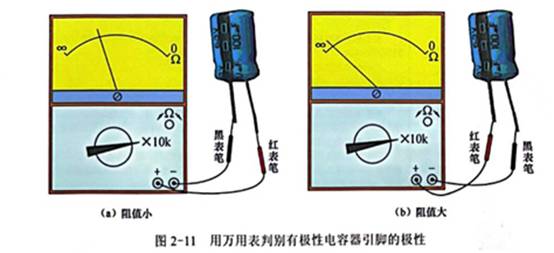
一个数字体系中往往需求多种频率的时钟脉冲作为驱动源,这样就需求对FPGA的体系时钟(频率较高)进行分频。比如在进行流水灯、数码管动态扫描规划时不能直接运用体系时钟(太快而肉眼无法辨认),或许需求进行通讯时,由于通讯速度不能太高(由不同的规范限制),这样就需求对体系时钟分频以得到较低频率的时钟。
分频器首要分为偶数分频、奇数分频、半整数分频和小数分频,假如在规划过程中选用参数化规划,就能够随时改动参量以得到不同的分频需求。
在对时钟要求不是很严厉的FPGA体系中,分频一般都是经过计数器的循环计数来完成的。
偶数分频(2N)
偶数分频最为简略,很容易用模为N的计数器完成50%占空比的时钟信号,即每次计数满N(计到N-1)时输出时钟信号翻转。
奇数分频(2N+1)
运用模为2N+1的计数器,让输出时钟在X-1(X在0到2N-1之间)和2N时各翻转一次,则可得到奇数分频器,可是占空比并不是50%(应为 X/(2N+1))。
得到占空比为50%的奇数分频器的根本思维是:将得到的上升沿触发计数的奇数分频输出信号CLK1,和得到的下降沿触发计数的相同(时钟翻转值相同)奇数分频输出信号CLK2,
最终将CLK1和CLK2相或之后输出,就能够得到占空比为50%的奇数分频器。原理图如下:
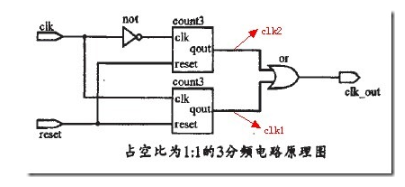
用Quartus II 得到的占空比为50%的9分频时钟输出信号outclk如下:
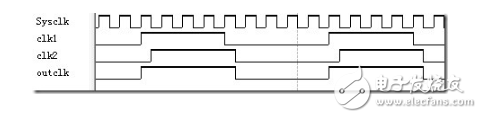
半整数分频(N-0.5)
根本规划思维为:首要进行模N的计数,计数到N-1时输出时钟翻转;并且在计数返回到0时,输出时钟再次翻转。
所以,只要使计数值N-1坚持半个时钟周期,即可完成N-0.5分频时钟。那么怎么坚持半个时钟周期呢?
由于计数器是上升沿触发计数,假如在计数值=N-1时把计数器的触发时钟翻转,则时钟的下降沿就变成了上升沿。即计数值=N-1时,时钟立刻翻转,
则计数值坚持半个时钟周期后,会遇到上升沿而使计数值归0. 然后计数器以翻转了的时钟持续计数,在发生N-0.5个分频周期后,时钟再次翻转。
2.5分频的时序示意图如下:
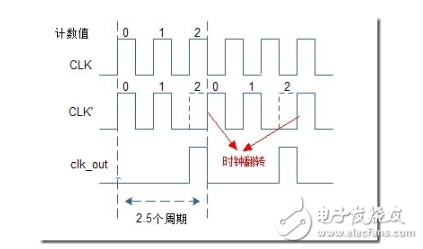
怎样才能够使计数器的触发时钟在N-1时翻转呢? 由半整数分频器的原理图可知,将输出时钟二分频后和输入时钟相异或就可使触发时钟翻转。
半整数分频器原理图如下:
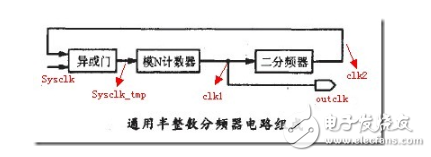
用Quartus II 完成的2.5分频时序图如下:
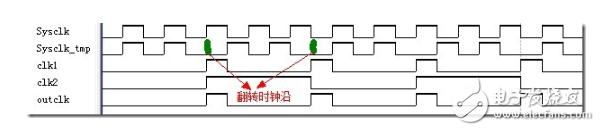
由通用分频器电路组成图能够看到,半整数分频器是由整数分频器加上二分频和异或门而构成的。
那么,假如运用元件例化的思维就能够得到通用的分频(即可挑选整数分频和半整数分频)。
假如想要得到恣意分频,则能够参阅CrazyBingo 的 使用DDS原理的 教你什么才是真实的恣意分频。