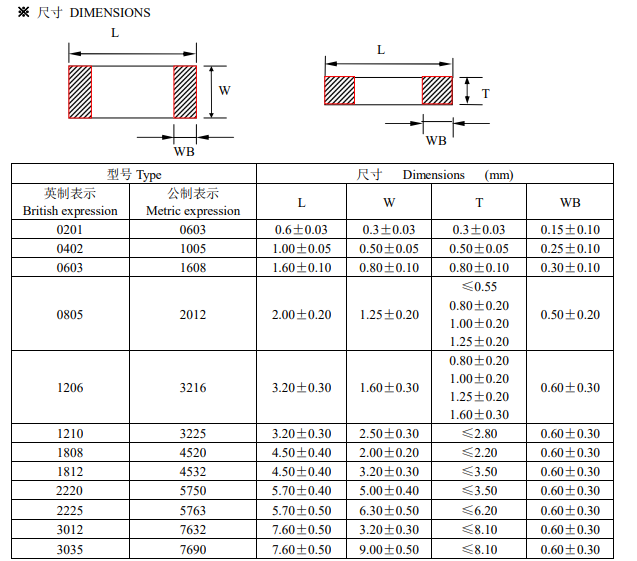
今日咱们来写状况机。
关于状况机呢,想必咱们应该都触摸过,浅显的讲便是数电里咱们学的状况转化图。状况机分为两中类型,一种叫Mealy型,一种叫Moore型。前者便是说时序逻辑的输出不只取决于当时的状况,还取决于输入,而后者便是时序逻辑的输出只是取决于当时的状况。下面两个图别离表明两种不同的状况机。
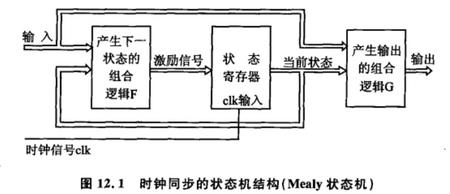
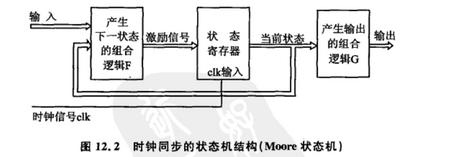
下面咱们就经过代码来写一下状况机,以下面的状况转化图为例
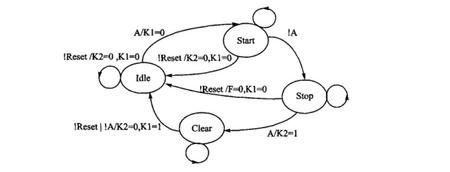
首要,是一种典型的状况机写法,这种写法咱们称为一段时状况机,用于一些简略的规划是能够的,但如果是杂乱的状况机,不主张咱们用这种写法。
//***********************************************************
//可归纳的状况机规划的典型办法
//完成典型的状况机规划
//**********************************************
module fsm (clk,rst_n,A,k1,k2,State);
input clk;
input rst_n;
input A;
output k1,k2;
output [1:0] State;
reg k1;
reg k2;
reg [1:0] State; //当时状况寄存器
parameter Idle = 2’b00,
Start = 2’b01,
Stop = 2’b10,
Clear = 2’b11; //编码 ,留意,只要在最终一句用分号,其他地方用逗号
always @(posedge clk or negedge rst_n)
if(!rst_n)
begin
State <= Idle;
k1 <=1’b0;
k2 <=1’b0;
end
else case (State) //状况判别与组合逻辑赋值
Idle :if(A) begin
State <= Start;
k1 <= 0;
end
else begin
State <= Idle;
k1 <= 0;
k2 <= 0;
end
Start :if(!A) State <= Stop;
else State <= Start;
Stop :if(A) begin
State <=Clear;
k2 <= 1;
end
else State <= Stop;
Clear :if(!A) begin
State <= Clear;
k2 <= 0;
k1 <= 1;
end
else State <= Clear;
default : State <= 2’bxx; //告知归纳器 case句子现已指定了一切状况,这样归纳器就会删去不需要的译码电路,使生成的电路简略
endcase
endmodule