滤波器的截止频率(F0 )一般地是指起伏呼应比通带低3 dB时的频率。关于切比雪夫滤波器, 有时能够界说为起伏呼应降至通带以外时的频率。例如, 一个0.1 dB切比雪夫滤波器的F0 能够界说为呼应下降》 0.1 dB 时的频率。 假如调查的是实践频率与截止频率之比,而不是实践频率 自身,则衰减曲线的形状(以及相位和推迟曲线,它们定 义着滤波器的时域呼应)将是相同的。将滤波器归一化至 1 rad/s,则可开宣布一种简略的滤波器规划和比较体系。 在此基础上,用截止频率对滤波器进行缩放,以确认实践滤波器的元件值。
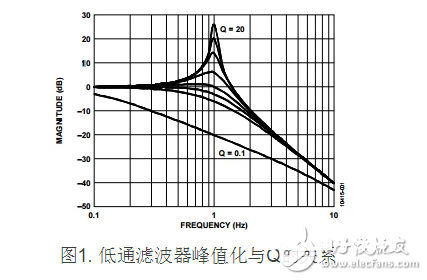
滤波器的品质因数(Q)有时也表明为α,其间: 这一般称为阻尼比。请注意,有时运用ξ,其间:若Q 》 0.707,则滤波器呼应中会有些峰值化现象。若Q 《 0.707,F0 处的滚降会稍大;斜率将更平整些,滚降发生的 时刻将提早。关于2极点低通滤波器的峰值化量与Q的联系如图1所示。
用ωo 和Q改写传递函数H(s):
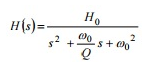
其间,H0 为通带增益且ωo = 2π F0 。 现在,咱们将用该低通原型来规划滤波器。
高通滤波器
把低通原型的传递公式H(s)的分子改为H0 s2 ,成果将使低 通滤波器变成高通滤波器。该高通滤波器的呼应在形状上 与低通滤波器类似,仅仅频率反相罢了。 高通滤波器的传递函数为:
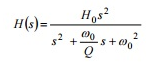
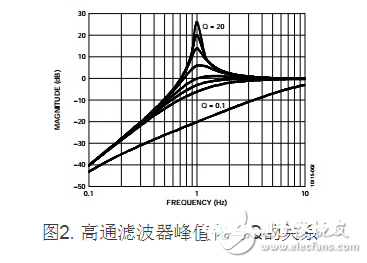
2极点高通滤波器的呼应如图2所示。
带通滤波器
把低通原型的分子改为Ho ωo 2 ,成果将把滤波器变成一个 带通函数。 带通滤波器的传递函数为:
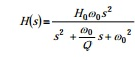 (5)
(5)
其间:ω为滤波器增益峰值化时的频率(F0 = 2 π ω0 )。 H0 为电路增益,界说为:
H0 = H/Q. (6)
对带通呼应来说,Q有特别含义。它是滤波器的选择性。 界说为:
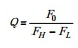 (7)
(7)
其间,FL 和FH呼应比最大值相差–3 dB时的频率。 滤波器的带宽(BW)界说为
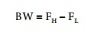 (8)
(8)
请注意,能够证明,谐振频率(F0 )为FL和FH的几何平均 值,这就意味着,F0 在对数规范大将出现在FL 和FH二者的中点。
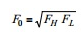
另需注意的是,在对数规范上,带通呼应的波裙在F0 左右 始终是对称的。
带通滤波器对各种Q值的呼应如图3所示。
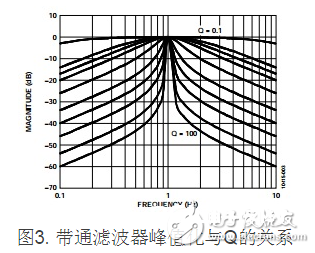
这儿需求提示一下。带通滤波器有两种界说方法。窄带情 况为经典界说,如图3所示。
但是,在某些状况下,假如高、低截止频率相差很大,则 带通滤波器选用独立的高通和低通部分进行结构。这儿所 说的相差很大是说至少相差2个倍频程(频率&TImes;4)。这是使 用宽带的状况。
带阻(陷波)滤波器
把分子改为s2 + ωz 2 ,就能够将滤波器转换成一种带阻或陷 波滤波器。就如带通滤波器相同,假如带阻滤波器的转机 频率之间距离大于一个倍频程(宽带状况),则可用独自的 低通和高通部分结构。因而,咱们将选用以下规范:窄带 带阻滤波器将称为陷波滤波器,宽带带阻滤波器称为带阻 滤波器。
陷波(或带阻)传递函数为:
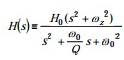 (9)
(9)
陷波滤波器的特性有三种状况,如图4所示。极点频率ω0 与零点频率ωz 的联系决议着滤波器是规范陷波、低通陷 波,仍是高通陷波。
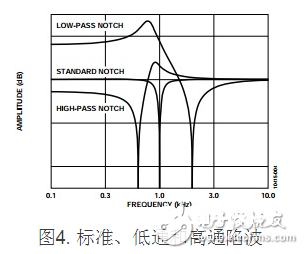
假如零点频率等于极点频率,则存在规范陷波。在此例 中,零坐落jω平面,其间,界说极点频率的曲线与轴相 交。
当零点频率大于极点频率时,会发生低通陷波。这种状况 下,ωz 坐落极点频率曲线之外。对实践使用来说,这意味 着,滤波器在ωz 以下的呼应将大于ωz 以上的呼应。成果形 成一种椭圆形的低通滤波器。
当零点频率小于极点频率时,会发生高通陷波滤波器。这 种状况下,ωz 坐落极点频率曲线之内。对实践使用来说, 这意味着,滤波器在ωz 以下的呼应将小于ωz 以上的呼应。 成果构成一种椭圆形的高通滤波器。
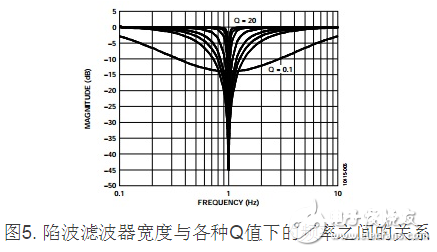
陷波宽度随Q的改变状况如图5所示。