0导言
两个同频信号的相位差丈量在工程上有着广泛的使用。近年来,精细丈量、雷达定位、方针辨认等范畴的高速开展对相位差丈量精度和速度都提出了很高的要求。现在,理论上比较老练的相位差丈量算法首要使用相关原理和快速傅里叶变换(FFT)原理。但由于硬件环境的复杂性和不稳定性,传统硬件丈量的精度往往大大低于软件计算精度,而高功能FPGA芯片的开展为硬件进步相位差丈量算法的精度供给了新的方向。
本文首要介绍了两种相位差丈量算法,一种是依据直接数字频率组成(DDS)的相关丈量法,另一种是依据快速傅里叶变换的FFT丈量法。在软件仿真的基础上,使用高功能的FPGA芯片建立硬件试验渠道,完成了两种算法的硬件完成。
1算法原理和理论仿真
1.1相关丈量法
首要在接纳端使用本振信号与接纳信号进行相关,再通过数字低通滤波器滤除高频重量,别离得到两路接纳信号的相位信息,最终相减得到相位差。由于噪声与本振信号相关性很小,所以可以很好地加以按捺。设被测信号为:
式中:f0为被测信号频率;φ1,φ2别离为两路信号的相位。两路信号的相位差△φ=φ1-φ2,即为所求。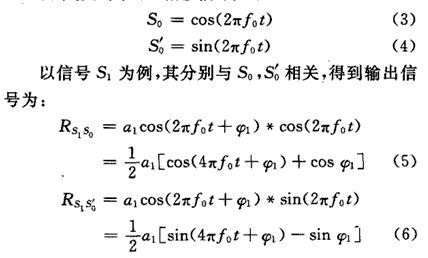
式中,a1为相关后输出信号的起伏,由于两路本振信号的起伏共同,故相关后输出信号的起伏也可以为持平,通过低通滤波器滤除高频重量后可得:
1.2FFT丈量法
假定两路接纳信号同式(1),式(2)所示,则信号Si(n)(i=1,2)在通过FFT之后得到离散频谱Si(k),其频率地点点的谱线的实部和虚部别离包含了信号相位的余弦信息和正弦信息。依据快速傅里叶变换的FFT丈量法正是使用这两项信息别离求得两路被测信号的相位值,最终相减得到相位差。由于噪声是宽带的,在被测信号频率点处的噪声搅扰影响并不大,不会产生很大搅扰。FFT是离散傅里叶变换(DFT)的快速算法,依据DFT的原理:
式中:i=1,2;k0可通过在FFT频谱上查找最大值的办法确认。最终将两路被测信号的相位差值相减即可得到相位差△φ: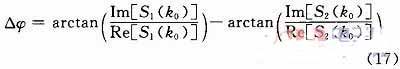
1.3理论仿真
在PC环境下用Matlab软件仿真两种相位差丈量算法的功能,别离就以下两种状况进行功能仿真:一是白噪声搅扰条件下,二是不同数据长度N条件下,这两项目标别离决议了丈量算法的高精度和实时性。假定两信号的相位差△φ为30°,被测信号频率f0为1MHz,数字采样频率fs为8MHz。
仿真成果如图1所示,其间图1(a)是在不同信噪比白噪声搅扰条件下两种丈量法的仿真成果比较;图1(b)是在不同数据长度N条件下两种丈量法的仿真成果比较。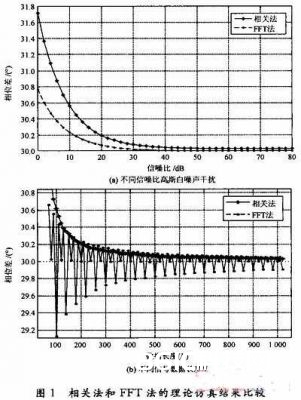
仿真成果表明,在较低信噪比高斯白噪声搅扰条件下,FFT丈量法对白噪声的按捺才能要强于相关丈量法,在高信噪比时两种算法均可到达较高丈量精度,其功能也趋于共同。在不同信号数据长度N条件下,相关丈量法的精度跟着N的添加而进步,FFT丈量法在N等于2的整数次幂的时分,其丈量精度要高于相关丈量法,在N不等于2的整数次幂的时分会产生由数据切断引起的频谱走漏,使其功能变差,这是由于要与硬件完成相统一,对一切数据长度均作2的整数次幂的FFT运算,所以在硬件完成的时分,FFT长度N应该控制在2的整数次幂。