数据收集,又称数据获取,是运用一种设备,从体系外部收集数据并输入到体系内部的一个接口。数据收集技能广泛引用在各个范畴。比方摄像头,麦克风,都是数据收集东西。被收集数据是已被转换为电信号的各种物理量,如温度、水位、风速、压力等,可所以模仿量,也可所以数字量。在互联网职业快速开展的今日,数据收集现已被广泛应用于互联网及分布式范畴,数据收集范畴现已发生了重要的改变。
而在数据收会集存在着各种噪声。滤除噪声的办法有很多种,既有数字滤波器,也有模仿滤波器。这儿咱们选用了根据单片机和C言语来规划并开发数字滤波体系。
咱们针关于单片机数据收集体系中常常呈现的随机搅扰,经过手动输入来模仿数据收集进程,验证了几种运用较为遍及的战胜随机搅扰的单片机数字滤波算法,并给出了相应的C程序,特别对中位值滤波和中位值均匀滤波算法程序进行了改善。一起也对这几种滤波算法进行了比较,并指出了每一种算法的详细适用规模和注意事项。别的咱们运用了 proteus进行仿真验证这几种滤波办法。别的咱们还运用了AD和DA来收集及输出数据。
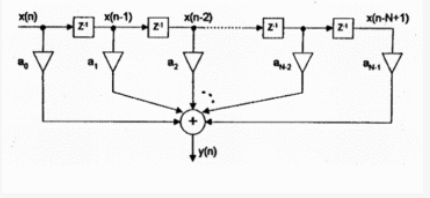
1 数字滤波规划原理
这儿有很多种数字滤波办法,咱们见选用其间几种来进行规划,如中值滤波、算术均匀滤波、加权均匀滤波等等。所以下面我将详细介绍它们。
1.1 中值滤波
中位值滤波是先对某一参数接连采样N次(一般N取奇数),然后把N次采样值按从小到大摆放,取中心值为本次采样值。
该滤波办法实际上是一种排序办法,我在此选用的是冒泡法排序。因为在冒泡法排序中,每呈现一次前者数据大于后者数据,就要进行二者数据的交流。
该算法的样比如程序如下:
1 #define N 11 //N值可根据实际状况调整
3 char filter()
5 {
7 char value_buf[];
9 char count,i,j,k,temp;
11 for(count=0;count
13 {
14 value_buf[count]=get_data();
17 delay();
18 }
20 for(i=0;i
22 {
k=i;
24 for(j=i+1;j
26 if(value_buf[j]
28 temp=value_buf[k];
30 value_buf[k]=value_buf[i];
32 value_buf[i]=temp;
34 }
36 return value_buf[(N-1)/2];
37 }
位值滤波能有用地战胜偶尔要素引起的动摇或采样器不稳定引起的误码等脉冲搅扰。对温度、液位等缓慢改变的被测参数选用此算法能收到杰出的滤波作用,但关于流量、压力等快速改变的数据,不宜选用中位值滤波。
1.2 算术均匀滤波
算术均匀滤波法适用于对一般的具有随机搅扰的信号进行滤波。这种信号的特点是信号本身在某一数值规模邻近上下动摇,如丈量流量、液位时常常遇到这种状况。算术均匀滤波法是要按输入的N 个采样数据,寻觅这样一个Y,使得Y 与各个采样值之间的误差的平方和最小。
详细完成此算法的子程序如下:
1 #define N 12
2 char filter()
5 {
7 int count;
9 int sum=0;
10 for(count=0;count
13 {
15 sum+=get_ad();
16 delay();
17 }
18 return (char)(sum/N);
19 }
算术均匀滤波适用于对一般具有随机搅扰的信号进行滤波。这种信号的特点是有一个均匀值,信号在某一数值规模邻近做上下动摇,在这种状况下仅取一个采样值做根据显然是不精确的。算术均匀滤波对信号的滑润程序彻底取决于N,当N较大时,滑润度高,但灵敏度低;当N较小时,滑润度低,但灵敏度高,应视详细状况选取N,以便既少占用核算时间,又到达最好的作用。
1.3 加权均匀滤波
在算术均匀滤波和移动均匀滤波中,N次采样值在输出成果中的权重是平等的,取1/N。用这样的滤波算法,关于时变信号会引进滞后,N值越大,滞后越严峻。为了添加新采样数据在移动均匀中的权重,以进步体系对当时采样值中所受搅扰的灵敏度,可选用加权均匀滤波,它是移动均匀滤波算法的改善。
加权均匀滤波是对接连N次采样值别离乘上不同的加权体系之后再求累加和,加权体系一般先小后大,以杰出后边若干采样的作用,加强体系对参数改变趋势的辨识。各个加权体系均为小于1的小数,且满意总和等于1的约束条件。这样,加权运算之后的累加和即为有用采样值。
为便利核算,可取各加权系数均为整数,且总和为256,加权运算后的累加和除以256,即舍去低字节后就是有用采样值。详细的样比如程序如下:
1 //code数组为加权体系表,存在ROM区。
2 #define N 12
3 char code jq[N]={1,2,3,4,5,6,7,8,9,10,11,12};
4 char code sum_jp=1+2+3+4+5+6+7+8+9+10+11+12;
5 char filter_5()
6 {
7 char count;
8 char value_buf[N];
9 int sum=0;
10 for(count=0;count
11 {
12 value_buf[count]=get_data();
13 delay();
14 }
15 for(count=0;count
16 sum+=value_buf[count]*jq[count];
17 return (char)(sum/sum_jq);
18 }
1.4 中位值均匀滤波
它适当所以“中位值滤波法”和“算术均匀滤波法”的结合。它接连采样N个数据,然后去掉一个最大值和一个最小值,最终核算N-2个数据的算术均匀值。一般N值的选取:3-14。
详细算法程序如下:
1 #define N 12
2 char filter()
3 {
4 char count,i,j;
5 char value_buf[N];
6 int sum=0;
7 for (count=0;count
8 {
9 value_buf[count] = get_ad();
10 delay();
11 }
12 for (j=0;j
13 {
14 for (i=0;i
15 {
16 if ( value_buf[i]》value_buf[i+1] )
17 {
18 temp = value_buf[i];
19 value_buf[i] = value_buf[i+1];
20 value_buf[i+1] = temp;
21 }
22 }
23 }
24 for(count=1;count
25 sum += value[count];
26 return (char)(sum/(N-2));
27 }
这种滤波办法兼容了移动均匀滤波算法和中位值滤波算法的长处,所以不管对缓慢改变的信号,仍是对快速改变的信号,都能取得较好的滤波作用。
1.5 限幅滤波
限幅滤波的基本原理是把两次相邻时间(n和n-1)的采样值Yn和Yn-1相减,求出其差值,以绝对值表明,然后将这个差值与两次采样答应的最大误差值ΔY比较,假如两次采样值的差值超越了答应的最大误差值ΔY,则以为发生了随机搅扰,并以为最终一次采样值Yn不合法,应予除掉。除掉Yn后,可用Yn-1替代Yn;若未超越答应的最大误差值规模,则以为本次采样值有用。可用如下公式表明:
|Yn-Yn-1|≤ΔY;则Yn有用
|Yn-Yn-1|>ΔY;则Yn-1有用
此算法的样比如程序如下:
此算法的样比如程序如下:
#define A 10 //A值可根据实际状况调整
char data; //上一次的数据
char filter_1()
{
char datanew; //新数据变量
datanew=get_data(); //取得新数据
//滤波算法
if ((datanew-data》A)||(data-datanew》A)
return data;
return datanew;
}
该算法首要用于处理改变比较缓慢的数据,如温度、物体的方位等。运用时关键在于最大误差值的Δy的挑选,一般可根据经历取得,也可依照输出参数或许的最大改变速度Vmax及采样周期T来决议ΔY的值,即ΔY=VmaxT。
1 #include
2 #include
3 #define uchar unsigned char
4 #define A 0.005
5 #define N 11
6 sbit con1 = P2^3;
7 sbit con2 = P2^4;
8 sbit con3 = P2^5;
9 sbit con = P2^6;
10 sbit OE = P2^0;
11 sbit START = P2^1;
12 sbit EOC = P2^2;
13 uchar a;
14 uchar buf[N] ={0};
15 void change()
16 {
17 int i;
18 for(i=0;i
来历;21ic