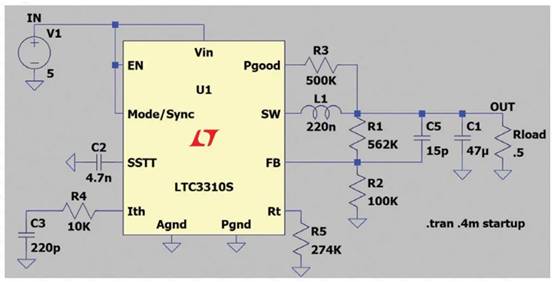
上一篇文章的理论延伸,咱们能够完结一个根本运用电路。依据了解运用该模仿信号链 的根本构建块所进行的运算。
的根本构建块所进行的运算。
该具有差动输入的高增益电路的称号起源于模仿核算机年代。每一个数学运算都需求一个放大器来将一个函数与下一个函数阻隔。简略来说,能够装备一个运算放大器 (op amp),以用于完结反相或非反相增益(见图 1)。
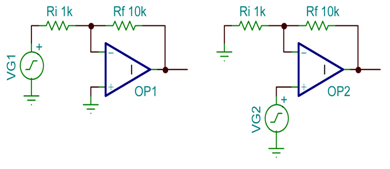
图 1 根本增益级
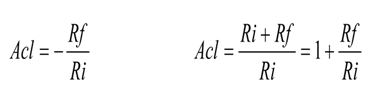
该增益方程式标明,当 Ri>Rf 时,反相级或许会有一个小于 1 的闭环增益 (Acl);当 Ri=Rf 时,该增益为 -1(反相),该非反相级绝不或许有一个小于单位增益 (unity) 的增益。当 Ri 为开路时,该电路就会简化为一个单位增益电压跟从器。假如需求一个小于 1 的增益,那么就应该在放大器前面放置一个电压分压器。
由于这是一个线性系统,所以适用线性迭加规律。因而,下面要讲的便是将两个或更多的信号累加起来(见图 2)。
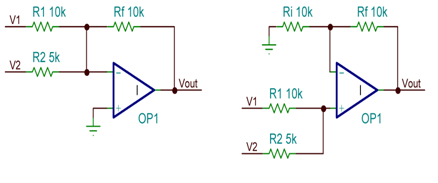
图 2 加权信号求和
为了树立这些联系,首要假定 V2=0,并以 V1 的一个函数写出 Vout 的方程式。然后假定 V1=0,并写出 V2 的方程式。将两项兼并就能够得到完好的传输函数。能够用此处所示的部分并联方法增加更多的输入,而且运用该迭加技能能够得出总传输函数。
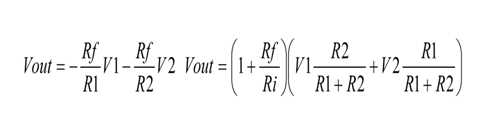
与方才的运算比较,这种可增加电压的才能更具价值。在一个规划中,许多时分都必须进行一个电平转化,而这些电路正好能够完结这一使命。经过这些求和的改变,也有或许完结补码运算(也即减法运算)见图 3。
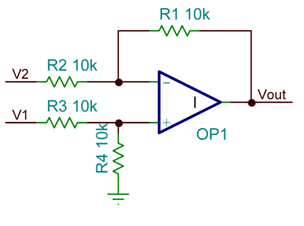
图 3 差动放大器 (diff amp)
如上那样运用线性迭加,该差动放大器的通用输出表达式为:

一种被广泛运用的运用是那些可用信号依存 (ride on) 于搅扰信号中的运用(见图 4)。搅扰信号被称作共模电压 (Vcm),由于其为两个输入共有,而抱负信号为差模电压 (Vdm)。在此情况下,其值为 Vdm1 与 Vdm2 的和。
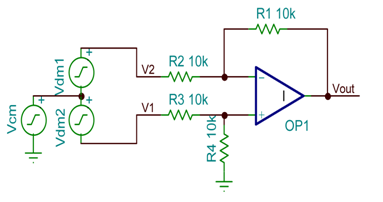
如图 4 差动放大器运用
假如 R1=R4 且 R2=R3,那么 Vout 可由下式得出:
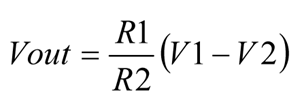
消除搅扰信号的精确度取决于两个变量:电阻器匹配的精确度和运算放大器的参数(被称为共模抑制比 (CMRR))。假定确实存在完美的运算放大器,那么电阻器不匹配导致的输出核算则为一道简略的电子表格核算题。
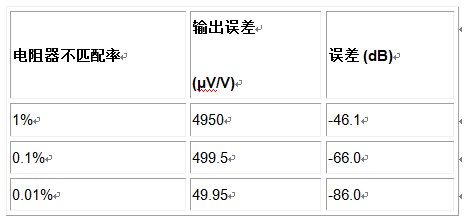
表 1 电阻器不匹配导致的输出核算
已然咱们已经有了一套根本构建块,那么接下来咱们就能够开端挑选各种可用的转化器了。