现在,FPGA作为可编程逻辑器件(PLD)的主要产品,在通讯、消赞电子、轿车电子、工业操控、国防安全等范畴得到广泛的使用。因为在功用和灵活性方面的完美组合,FPGA的使用范围越来越广,客观上要求加强FPGA数字处理功用(如嵌入乘法器,数字信号处理器(DSP)等)。现住简直每一款商用FPGA内部简直都嵌入了乘法器或数字信号处理器,如Xilinx公司的VirtexⅡ系列、Spartan-3/3A系列等。相对来说我国的FPGA只是处于起步阶段,FPGA的开展特别是高功用FPGA的开展刻不容缓。本文紧跟国家重大项目,对嵌入到FPGA的乘法器进行了深化的研讨提出了一个低功耗、高速度的乘法器。该乘法器选用了高速布斯译码、依据全加器的9-2紧缩树和35 b两级超前进位加法器。高速布斯译码器选用了改善的布斯算法,使得部分积通过3个门的推迟得到,进步速度约为50%;9-2紧缩树由3个3-2紧缩和一个4-2紧缩组成,使得部分积阵列仅通过7个异或门推迟;35 b两级超前进位加法器选用的是依据4 b超前进位加法器,使得加法器只是通过10个门的推迟。
1 全体结构
图1为18×18位乘法器的全体结构,它包含了布斯译码模块、紧缩树模块和超前进位加法模块。部分积是通过本文采纳的布斯译码器快速发生,然后其通过9-2紧缩树被紧缩成两个35 b的二进制数,终究通过超前进位加法器生成无符号位的35 b的成果。通过乘数和被乘数的符号位异或发生终究积的符号位,这样就得到了36 b的终究成果。从图1能够看出该乘法器全体结构和传统的结构是相同的。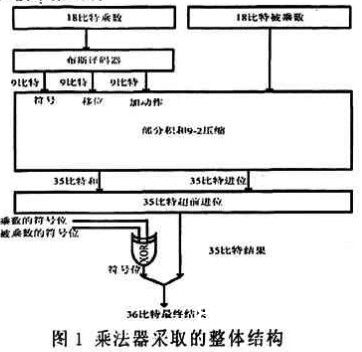
2 布斯译码和部分积
一般进行两个数相乘,是通过一切的部分积相加得到。这样,不只乘法器的速度都得不到确保,而且会糟蹋芯片的面积。因而采纳现在比较盛行的布斯算法,因为它能够使部分积的数目折半,这样对面积和速度都比较有利。在原算法的基础上进行了改善并得到一种新的布斯译码和部分积结构。咱们将布斯算法分解为“sig”,“sht”,“add”三个个因子,别离用来代表对被乘数的不同操作。其间“sig”用来决议被乘数是取反仍是坚持不变;“sht”代表是否对被乘数进行左移一位;而“add”则表明决议终究得到部分积。改善的算法用表达式表明则为:
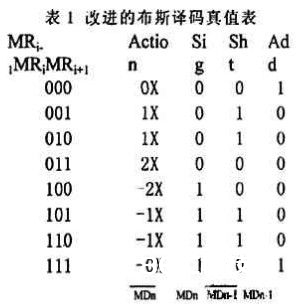
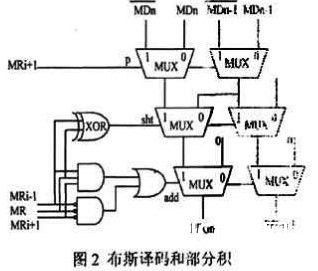
从图2能够看出,改善的布斯译码器由1个异或门、2个与门和1个或门构成而部分积则是有3个二选一多路选择器构成,其要害途径为3个门的推迟。因而结构要比传统的更为简略、推迟更小。
3 9-2紧缩树
华莱士树(Wallace Tree)算法通过并行相加来进步速度。在华莱士树中一切部分积列在同一时间各自独立的进行相加。选用的是一种依据保存进位全加器的9-2紧缩树用来紧缩部分积阵列的,在每一个9-2紧缩树的最顶层有9 b的部分积。9-2紧缩树顶用到了3个3-2紧缩和1个4-2紧缩。关于那些少于9 b的部分积列,为了进一步减小芯片面积,依据部分积的数目选用相应的紧缩树,而且能够用半加器用来替代3-2紧缩(全加器)。
典型的4-2紧缩是由2个3-2紧缩构成的,其推迟为4个异或。图3为一个优化了的4-2紧缩,其推迟为3个异或的推迟。因而9-2紧缩树从顶层到终究输出仅过了7个异或门的推迟。
4 35 b两级超前进位加法器
超前进位加法器对乘法器的全体功用的影响至关重要,要想进步乘法器的速度,超前进位加法器也有必要进行必要的优化。在此采纳依据4 b超前进位加法器的两级加法器。
因为进位链推迟时间跟着输入的添加而添加,有必要考虑到输入信号的个数,在面积和速度中进行折中发现4 b超前进位加法器是最适合作为根本的模块。
从图4(b)中能够看到在4 b超前进位加法器中,除了P和G由与门完成的,其他的都是有与非门完成的。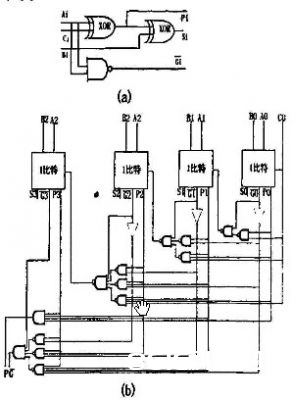
图4(a)为1位全加器的变形,有3个输入Ai,Bi,Ci和三个输出Pi,Si和Gi,其间Ai和Bi为两个加数,Cin为进位输入,Pi和Gi别离为进位传输和进位发生,而Si为第i位的和。
选用依据4 b的超前进位加法器来组成16 b超前进位加法器,进位链采纳与4 b超前进位链相同的结构。相同的剖析办法,发现16 b的P和G延时为5个门的推迟。用2个16 b的超前进位加法器和一个3 b超前进位加法器组成35 b超前进位加法器,其进位链采纳与上面相同的办法。研讨不难发现,通过7个门推迟进位抵达3 b超前进位加法器,再通过3个门的推迟得到第35位的成果。也就是说整个加法器只是通过10个门的推迟。
5 规划总结
5.1 归纳条件阐明
选用TSMC0.18μm CMOS工艺和Synopsis DC进行的归纳并进行推迟剖析。并在DC指令窗口输入了指令“set_dont_use”和“set_dont_ touch”。
5.2 布斯译码和部分积
把传统的布斯译码和部分积与本文采纳的布斯译码和部分积进行了比较,并把成果列在了表2中。从表中发现本规划要害途径与OhkuBo比较减少了50%,生成部分积的速度相应的进步了50%。
5.3 与其他的乘法器进行比较
本文的乘法器与表3中乘法器比较速度有明显进步,与Xilinx公司的Spartan-3A系列嵌入到FPGA的乘法器比较本文乘法器的速度更进步40%。更为要害的是在没有添加芯片面积的情况下把速度进步40%。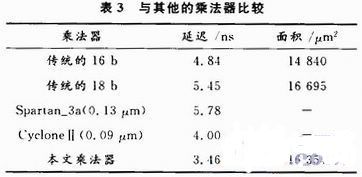
6 结语
本文依据改善的布斯算法的18×18乘法器是特意为嵌入到FPGA而规划的,它处理了乘法器占用FPGA较多资源的问题,并为今后DSP嵌入到FPGA做了必要的准备工作。选用了一种新的布斯译码和部分积、9-2紧缩和两级超前进位加法器以使乘法器到达较好的功用。通过仿真验证,这儿提出的依据改善的布斯乘法器各项目标均能很好的满意嵌入到FPGA的要求。