RS纠错编码是现在最有用、运用最广泛的过失操控编码之一,是一种纠错才能很强的多进制BCH码,也是一类典型的代数几许码。它是由里德(Reed)和索洛蒙(Solomon)运用MS多项式于1960年首要结构出来的。
RS码被广泛用于过失操控体系中,以进步数据的可靠性,并且能够用来结构其他码类,如级联码。在无线通信、卫星通信、磁或光存储以及网络通信中RS码也有较为广泛的运用。RS码不只具有杰出的随机纠错和突发纠错才能,并且有低复杂度的编译码算法,因而被世界电信联盟(ITU)引荐为光纤子体系的前向纠错(FEC)码。RS(225,223)码被CCSDS选为惯例分包遥测信道纠错编码和高档在轨体系前向和反向链路的纠错编码,是完结CCSDS规范低过失率信道纠错编码的要害部件。只需每个码字(255个符号)中呈现的过错不超越16个符号,它就能将其纠正。
近年来,关于RS(255,223)码译码器完结的算法得到了广泛的重视,可是这些算法的完结速度都不太快,即使有速度稍高的,其占用硬件资源也较多,而一些占用硬件资源较少的算法速度却很慢。本文选用依据ME算法的8倍并行规划计划,结合流水线技能,克服了上述算法的缺点,运用尽可能少的硬件资源获得了极高的译码速度。
1RS(255,223)码及其译码原理
1.1RS(255,223)码
因其码元取自GF(q),RS编解码进程中的一切运算都是在GF(q)的有限域上面进行。RS(n,k)码的编码进程是将k个输入信息码字,用生成多项式发生(n,k)个冗余的纠错信息码字,与原码字组成构成n个信息码字进行传输。译码是在接纳端,对接纳的n个码字信息进行纠错处理,康复k个信息码字。关于1个长度为am-1符号的RS码,每个码字都能够看成是有限域GF(am)中的1个元素。最小码距为d的码字,其RS码生成多项式具有如下方式:
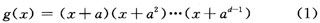
其间ai是GF(am)中的1个元素。
关于RS(255,223)码而言,q=256,a=2,码字符号在GF(28)中。m=8,是每个RS符号的码元数;n=28-1,是每个RS码字的符号数;k=223,是RS码中信息位的符号数;t=16,是RS码字内符号的纠错才能;d=33,是最小码距。
1.2RS(255,223)码译码原理
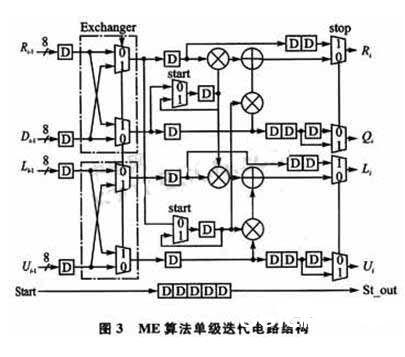
因为RS码为分组码,故其译码算法主要由随同式核算、要害方程求解和钱查找和Forney算法3部分构成,译码器结构如图1所示。
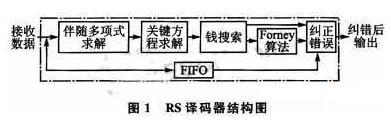
首要,依据接纳码字乘以校验矩阵得到其随同多项式,关于RS(225,223)码,其随同式求解式能够表明为:
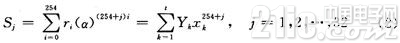
求得随同式今后,则运用随同多项式求解要害方程:过错方位多项式σ(x)和过错特征多项式ω(x),如下所示:
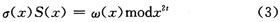
求解要害方程现可选用的算法主要有BM(Belekamp-Messey)算法和ME(ModifiedEuclidean)算法。之后便得到过错方位多项式σ(x)与过错特征多项式ω(x)。
尔后,由过错方位多项式与过错特征多项式来求得过错方位与过错值。求解过错方位本规划选用穷举算法DD钱查找算法来完结。一起,运用Forney公式求得过错值。最终,用延时后的接纳值减去过错值,得到最终的译码输出。Forney公式能够表明为:

其间,ei代表发生在i方位上的过错值,σodd(x)代表过错方位多项式奇数次项之和。
2并行流水结构计划
本规划选用8倍并行流水计划。将255个码元8倍并行后,只需要32个周期便完结一切32个随同多项式系数的求解。然后将32个随同多项式系数次序输出到下一级,在此基础上选用流水线结构,周期刚好满意且不会浪费资源。本规划中一切乘法器都是选用GF(28)有限域乘法器。
2.1随同式核算
8倍并行随同多项式的求解算法,是在迭代算法的基础上打开完结,其推导进程如下:
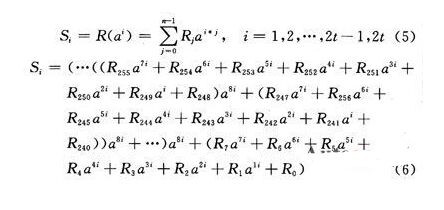
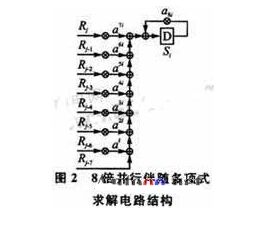
式(6)中,R255=0;i=1,2,…,2t-1,2t。其电路结构如图2所示。
2.2要害方程求解
本规划中要害方程的求解选用ME算法。BM算法具有反应结构,不适合运用流水结构,而ME算法可选用流水结构。其算法描绘如下:
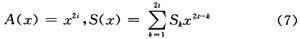
其间,S(x)为输入的随同多项式。
ME算法为1种迭代算法,意图在于求i阶余式Ri(x),相应的多项式ri(x)与Li(x)满意:
ri(x)A(x)+Li(x)S(x)=Ri(x)(8)
当i阶余式Ri(x)的阶数小于t时,迭代算法完毕。算法完毕时的Ri(x)即为过错特征多项式ω(x),而Li(x)即为所求的过错方位多项式δ(x)。
ME算法在每一次迭代时进行的运算为:
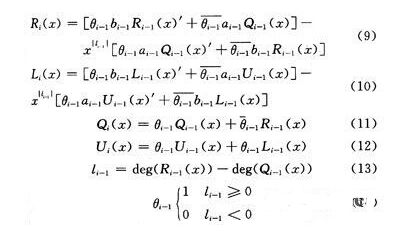
详细推导请见参考文献[8-9]。
单级迭代电路结构如图3所示。