在对任何信号进行傅立叶剖析时,得出的频谱为复数,且其频率规模将从-∞~∞。关于负频率以及该规模的频谱,应当怎么了解?它有没有物理含义?是一个还缺少评论,因而没有一致观点的问题,本文将对此进行评论。
摘要:本文评论了信号通过傅立叶改换所得频谱的物理含义,其间着重于负频率成分。许多信号与体系的教材中,都以为负频率成分没有物理含义。本文以多方面的实例证明了负频率成分不光具有清晰的物理含义,并且有重要的工程使用价值。文章还用Matlab程序演示了怎么用几许办法求傅立叶反改换,把集总频谱组成为时域信号,从中也可明显地看出负频率成分的含义。

1.负频率与复信号
频率 f 的原始界说是每秒呈现的次数,可用以衡量机械运动、电信号、甚至任何事情重复出。
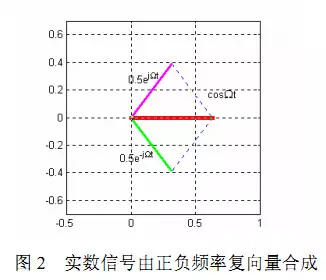
(a) 三维图形
(b)x-y 平面的二维图形现的频度,这当然不存在
有“负”的概念。当用频率描绘圆周运动时(即进入了二维信号平面),发生了角频率 ω”的概念,从机械旋转运动动身,界说为角速度,关于周期运动,角速度也便是角频率。一般 θ以反时针为正,因而滚动的正频率是反时针旋转角速度,负频率便是顺时针旋转角速度。正、负号是十分天然构成的,没有物理含义的有无问题。电的单位向量(电压或电流)环绕原点的滚动,可以用表明,这是在电路中都清楚的。θ的正负所代表的物理含义从未有什么争议,它的导数的物理含义不言自明,取正取负都不影响界说,为什么取负就会失掉物理含义了呢?在信号与体系课程中,为了简化问题,便于初学者把握概念,开宗明义地把研讨规模限定于实 信 号 f(t) , 也便是 在 电 压 旋 转 向 量中,只研讨它在实平面或虚平面上的一个投影 sin(ωt)或 cos(ωt),研讨复信号的特性与只研讨实信号 sin(ωt)或 cos(ωt) 是两个不同的层次。前者是反映信号在空间的全面特性,如图1 所示。后者只研讨了信号在一个平面(x-t或y-t组成的平面)上投影的特性。这就必定要丢掉一些重要的信息,致使 x=sin(ωt) 与sin(-ωt)在x-t平面中的波形没有任何不同,这是人们对负频率的含义发生疑问的直接原因之一。很显然,在x-t或y-t的平面内,是不或许看出旋转的。既看不到θ,更看不到ω。只要在x-y平面上才干看到这两个旋转参数。
2.复信号与实信号的频谱
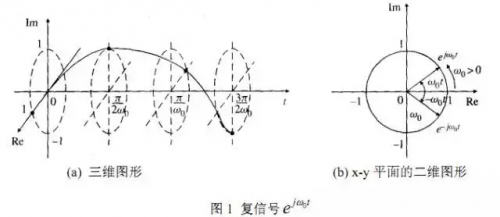
相同,用ejtω或 sin(ωt)或 cos(ωt)作为核来做傅立叶改换所得的成果也是前者全面,后者片面。对实信号做傅立叶改换时,假如用指数为核,将得到双方频谱。以角频率为Ω的余弦信号为例,它有具有坐落±Ω两处的、起伏各为 0.5、相角为零的频率特性。它的几许联系可以用图2表明。两个长度为 0.5 的向量,别离以±Ω等速滚动,它们的组成向量便是沿实轴方向的余弦向量。而沿虚轴方向的信号为零。可见必须有负频率的向量存在,才或许构成纯 粹的实信 号 。 所以欧公式是有其清晰的几许含义(即物理含义)的。在文献[1]中给出了动画,并给出了正、负数字频率的几许解说。