您或许知道,有用位数 (ENOB) 和有用分辨率都是与 ADC 分辨率有关的参数。了解它们的差异并确认哪个更具相关性,是令 ADC 用户与使用工程师等极为困惑的问题,常常因而发生争辩。
您以为哪个更重要?
ADC 的分辨率位数 (N) 可决定 ADC 的动态规模 (DR),其代表 ADC 可丈量的输入信号等级规模,一般以 [dB] 为单位。DR 可定义为:
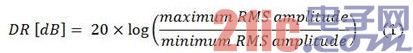
请注意,因为信号在给定时刻视窗内的 RMS 幅值取决于信号幅值在该时刻视窗内怎么改动,因而 ADC 的 DR 改动取决于输入信号特征。关于其满量程规模 (FSR) 内的稳定 DC 输入而言,抱负的 N 位 ADC 可别离丈量 FSR 和 FSR/2N 的最大及最小 RMS 幅值。因而,ADC 的 DR 为:
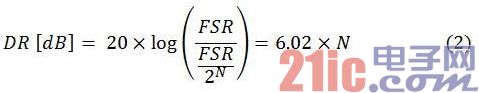
同理,关于幅值随 ADC FSR 改动而改动的正弦波信号输入而言,抱负的 N 位 ADC 可丈量 (FSR/2)/√2 的最大 RMS 幅值。正弦波输入信号的最小可丈量 RMS 幅值受量化差错的约束,其近似于幅值为半个 LSB 或 FSR/2N+1 的锯齿波。幅值 A 的锯齿波 RMS 幅值为 A/√3。因而,正弦波输入信号的抱负 ADC 的 DR 是:

真实的 ADC 具有可下降 DR 的差错。事实上,依据输入信号特征的不同,在输入信号挨近其最小值时,ADC 输出有不同类型的差错占主导地位。
关于稳定 DC 输入而言,ADC 的输出差错首要取决于所谓的“过渡”噪声,其包括 ADC、ADC 驱动器以及电源等组件的固有宽带散热噪声。假如 ADC 不存在较大的线性 (DNL) 问题,过渡噪声可在 ADC 输出端发生一个近似高斯代码散布。
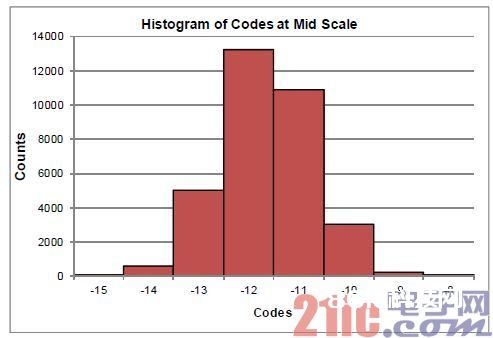
图 1:稳定 DC 输入的 ADC 输出代码直方图
本直方图的一个标准偏差 (σHISTO) 相当于过渡噪声的 RMS 值。在 σHISTO > 1 LSB 时,ADC 的 DC DR 就会减小至:

将 (2) 和 (4) 组合起来,可从头核算出下降的分辨率或有用分辨率:

同理,关于时刻改动的输入而言,ADC 的输出包括动态差错(即量化噪声与失真)以及可下降 DR 的过渡噪声。改动后的 DR 一般被称为 SINAD,从头核算的 ADC 分辨率被称为 ENOB。因而:

总归,给定 ADC 或许具有不同的 DR 和分辨率,首要取决于输入是 AC 仍是 DC 信号。因而,ADC 分辨率有独自的衡量目标,其对应于不同的输入条件,即 ENOB 对应于 AC 输入,有用分辨率对应于 DC 输入。确认哪种更适合天然取决于您的使用。









