作者:刘春江,吴智勇,于新,施玉海
1 导言
低密度奇偶校验(Low Densitv Paritv Check,LDPC)码已成为当今信道编码范畴的研讨热门之一。LDPC码归于线性分组码,根据其结构办法和相应的编码算法,首要分为两类:一类是随机结构的LDPC码,该类码在长码时具有很好的纠错才能,但是因为码组过长,以及生成矩阵与校验矩阵的不规矩性,使编码过于杂乱而难以用硬件完结,编码时刻过长也不利于硬件的实时运用;另一类是结构码,它由几许、代数和组合规划等办法结构。大多数LDPC结构码是循环或准循环结构,准循环码在中短码时具有恰当强的纠错才能,功能挨近随机结构的最优LDPC码,又因其硬件完结极端简略,只需用反应移位寄存器衔接就可完结,因而具有很好的运用远景。
在LDPC码的理论和运用研讨越来越遭到人们重视的一起,讨论LDPC码在DSP,VLSI(超大规模集成电路)和FPGA(现场可编程门阵列)等上的完结也成为一个重要研讨方向。在科研项目的工作中,发现一种针对准循环LDPC码的快速编码完结办法,关于码长为15 360的LDPC码,根据Altera公司的EP2S60型FPGA芯片完结时可到达25 Mbit/s以上的编码速度。
2 LDPC码的通用编码办法
作为信道编码中纠错才能最强的码型之一,LDPC码因为其译码器结构完结简略,能够用较少的资源消耗取得很高的吞吐量,但编码器的杂乱度问题作为不利要素限制着LDPC码的运用。传统的编码办法是经过生成矩阵生成码字,其杂乱度和码长的平方成正比,这使得LDPC码在编码上需求很多的硬件资源和很长的延时。Richardson在文献[4]中引入了一种新颖的算法在很大程度上处理了该问题,之后,Dong-U Lee等人运用这种新算法规划了相应的编码办法,这种编码办法适用于大多数的LDPC码;而关于根据有限几许或其他置换办法等结构出的具有循环或准循环特性的LDPC码,因为其特别的结构,可简略地用移位寄存器来完结编码,编码算法杂乱度进一步下降。
2.1 传统算法
LDPC码的传统编码算法和一般的线性分组码非常相似,需求求出生成矩阵。若已知长度为k的输入信息向量M,以及k×n的生成矩阵G,码字C就能够得到:C=M×G。在取得校验矩阵H后,运用H和G之间的正交性能够用高斯消元法来得到生成矩阵G。假定稀少矩阵H有如下办法:H=[H1 H2],其间H2是一个(n-k)×(n-k)的稀少方阵,并且在二元域上对错奇特阵,那么G就可用式(1)给出
![]()
很简略验证:这样的G满意HGT=0,其间,Ik是一个k阶的单位矩阵,这样得到的码字具有体系码的办法。
该编码算法可简略归纳为:若LDPC编码器将长度为k的信息比特m=(m0,m1,…,mk-1)编码为一个长度为n的LDPC码字C=(m,p)=(m0,m1,…,mk-1,p0,p1,…,pn-k-1),其间p为校验位,设LDPC码的奇偶校验矩阵为H=[H1,H2],其间,H1子矩阵包含H矩阵中的前k列,H2子矩阵包含H矩阵中的后n-k列,则由式(1)及C=mxG可得校验位
![]()
已知校验矩阵H求解生成矩阵G的首要算法是二元域上的高斯消元法,一般来说,这样得到生成矩阵G不是稀少矩阵,因而在编码时所用到的矩阵乘法的运算量阶数是O(N2)。
2.2 根据RU算法的编码办法
Richardson和Urbanke指出经过对LDPC的校验矩阵进行必定规矩的线性操作即预编码的算法(RU算法),能够使LDPC编码器的杂乱度控制在与码长成线性关系。设码字矢量x=(s,p1,p2),其间s为信息位,p1与p2合起来表明校验位,运用校验方程Hx′=0来核算p1和p2。RU算法首要包含预处理和实践编码两个进程。预编码经过队伍改换把校验矩阵H转化为近似的下三角阵办法H′,预编码只需履行一次,能够在软件中预先处理。然后把H′分红6个稀少矩阵,经过分步核算求得p1和p2,其间p1杂乱度为O(N+g2),p2的核算杂乱度为O(N)。图1为H经预编码后的近似下三角阵办法H′。
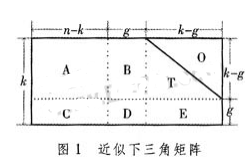
但怎么得到这个近似下三角矩阵仍没有令人满意的办法,T.J.Rrichdson等人经过贪心算法重排校验矩阵过于杂乱,且这样的预处理需求很长时刻。特别当码长较长时,这种编码办法不是一种抱负的完结办法。
2.3 准循环LDPC码及其编码办法
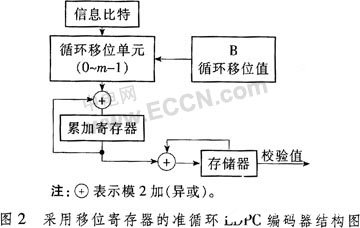
准循环LDPC码是一类结构比较特别且运用规模越来越广的LDPC码,其校验矩阵Hqc由一系列的m×m小循环方阵组成,这些小循环方阵能够是置换矩阵或是根据有限几许的矩阵等。因为Hqc的准循环特性,能够得到具有体系码办法和准循环特性的生成矩阵,即经过式(1)所得到的生成矩阵具有准循环特性,则只需求选用移位寄存器即可完结输入信息和生成矩阵的编码运算。针对一些特别的准循环LDPC码,D.E,Hocevar等人还提出一种仅运用校验矩阵即可用移位寄存器进行快速编码的办法,其结构如图2所示。B中存储着用来和信息比特相乘的循环移位值,循环移位单元在每个时钟周期循环右移或许左移一次。从完结的低杂乱度考虑,它优于根据RU算法的LDPC编码方案,但它只适用于具有准循环特性的LDPC码。
3 准循环LDPC码的快速编码办法
对准循环LDPC的编码完结可分为如下3个进程:
1) 核算中心变量DT=H1mT,根据H1矩阵具有准循环特性,运用循环移位寄存器完结,并对DT加以缓存。
2) 核算校验位
![]()
,这一步是整个编码算法中杂乱度最高也是最消耗资源的部分。
3) 取得编码后的码字C=(m,p)。
常用的编码算法因经过高斯消去法取得的H2-1既不是稀少矩阵,又不具有显着的准循环特性,因而形成第二步运算进程中运算杂乱度较高,下降了运算速度,影响了全体编码速度和功率。此刻,本文针对H2列重小于4的准循环LDPC码(一般H2矩阵的列重均较小),介绍了该类码的快速编码算法,进一步简化了编码杂乱度,以恰当添加资源占用为价值,极大地进步了编码速度。
3.1 快速编码办法
根据FPGA渠道,在对一类码长为15 360,行重为5~25,列重为2~12的准循环非正则LDPC码(其间每个子循环块的巨细为32×32),依照如下进程进行编码:
1) 第一步求DT=H1mT的运算,因为H1矩阵为准循环矩阵,只需将信息序列m以32个bit为单位依照H1矩阵中循环子矩阵的要求进行循环移位操作就可完结运算进程,用FPGA完结时只需一个时钟的时刻。
2) 进行第二步运算时,根据Ibrahim N.Imam等人提出的选用舒尔分化求解大矩阵逆矩阵的算法求解H2的逆矩阵H2-1可得:若用字符a表明32×32循环矩阵块为单位矩阵,字符b表明32×32单位矩阵各行别离循环右移一位所得的矩阵,字符c表明32×32单位矩阵各行别离循环右移两位所得的矩阵,则H2-1矩阵一切元素只要a/u,b/u,c/u,(b+c)/u,(a+b)/u,(a+c)/u这6种类型,其间u=a2+ab+b2。清楚明了:将公因子u提取出来今后,H2-1矩阵中的一切元素都可由a,b,c这3个符号或其加法之和组成,而二进制加法可简略地用异或门完结。这样H2-1DT的运算就可由最简略的移位寄存器和异或门构成,终究再用组合逻辑完结除以公因子u的运算,完结了准循环LDPC码的编码进程。整个编码算法的数据流程如图3所示。
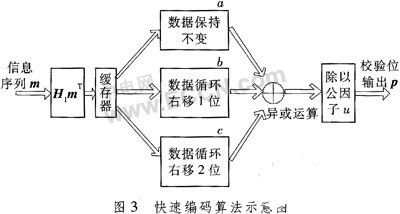
其详细运算进程为:将日H2-1矩阵分红a,b,c 3部分独立存储,若H2-1矩阵相应方位含有元素a,则将a存储区相应方位1,不然置0,同理完结对b和c存储区的初始化,完结第一步运算的中心成果参加第二步运算时,若a存储区某方位为1,则数据坚持不变参加后边的三输入异或运算,若该方位为0,则将一切数据置为0参加运算,同理若b存储区某方位为1,则数据右移1位后参加后边的三输入异或运算,若c存储区某方位为1,则数据右移2位后参加后边的三输入异或运算,为0则将数据置为0参加异或运算,移位和异或运算可在1个时钟周期内完结,终究除以常数公因子u的运算可用组合逻辑完结,不占用时钟周期。
将H2-1矩阵分红3部分存储今后,选用流水线结构,将本来需求10个时钟周期左右的运算进程缩短到最多4个时钟就能够完结,整个运算进程中除了存取数据外,只要移位操作和异或运算,大大进步了运算速度,一起也下降了编码的杂乱度,并且因为选用了恰当的存储办法,尽管分红3部分存储,但对存储资源的占用并没有太大添加,所消耗的逻辑运算单元仅略有添加。
3.2 快速编码办法的长处
本文介绍的快速编码办法的实质便是根据式(2)对准循环LDPC码进行编码求取校验位时,将H2-1采纳一种最合理有用的办法加以存储,一起将整个求解进程简化为只要寄存器移位和异或运算。因为准循环LDPC码的校验矩阵Hqc由一系列的m×m小循环方阵组成,选用舒尔分化法求得的H2的逆矩阵H2-1中只由少量几个元素或其加法组合构成,因而,关于一切准循环LDPC码均能够选用如图3所示的快速编码算法加以完结。该完结算法中只要循环移位和异或运算,且每次运算可一起对m个信息位进行处理。因而,选用快速编码算法不仅可完结线性时刻内编码,且其运算次数为O(N/m),下降了LDPC编码的时刻杂乱度。
4 小结
跟着集成电路技能和加工工艺的不断发展,大规模集成电路的逻辑资源数量呈几许级数添加,特别是FPGA芯片的逻辑单元数量已到达数百万数量级,但运算速度虽有很大进步却受制于物理结构和加工工艺等要素不能呈倍数的添加。本文提出的准循环LDPC快速编码算法根据“面积换速度”的规划原则,经过恰当添加对逻辑资源的占用,下降了运算杂乱度,极大地进步了运算速度,且该办法关于准循环LDPC码具有通用性,关于运用越来越广泛的准循环LDPC码的编码具有重要的参考价值。
责任编辑:gt









