作者 王科竣 电子科技大学(四川 成都 610054)
摘要：提出了一种新式的可调死区时刻发生电路。该死区发生电路是经过改动电压斜坡的斜率来调整死区时刻，并且对死区时刻与操控电压的非线性进行补偿，提高了死区时刻线性度和精度。该电路结构简练、可调规模广、精度高，适用于各种半桥驱动电路中。选用华虹0.5 μm的BCD工艺仿真验证了该电路，成果表明，当外接电阻阻值为20 K～140 K规模内，能够完成死区时刻的线性高精度可调，可调死区时刻规模为50 ns～250 ns。
0 导言
死区时刻发生功用广泛使用于各种驱动电路中，如在半桥电路[1]或同步整流变换器[2]中，为了避免电路中两个功率MOS管一起导通焚毁，在高压侧(续流管)的驱动信号和低压侧(主)驱动信号有死区时刻要求。此外在有源钳位正激变换器中，为了完成ZVS(零电压开关)驱动信号需求满意必定的死区时刻要求以使得功率功率MOS管的输出电容和变压器绕组的电感谐振[3]。死区时刻在不同的使用场合或许并不相同，这与电路中要驱动的功率管特性相关，需求依据状况调整。因而可调的死区时刻能够扩展驱动电路的适用规模。相对于文献[4][5]传统的死区发生电路，本文提出的可调的死区发生电路结构简练，经过调理外接电阻发生固定的死区时刻，具有更好的适用性。
1 电路结构和作业原理
本文提出的死区发生电路结构如图1所示。 图1中的死区发生电路是由Vin1的上升沿延时电路和Vin2的下降沿延时电路组成的。这两种功用的切换由Vsel端操控。图1中的DSC(delay stage C )为延时斜坡发生电路，CSA(controller stage A)和CSB(controller stage B)是曲率校对电路并且把死区时刻由电压操控(Vc1,Vc2)调整为电阻操控。当Vsel为高电平时，M3c处于导通状况，M4c处于封闭状况，此刻CSA和DSC左半部分的正常作业。相反，当Vsel为低电平时，M3c处于封闭状况，M4c处于导通状况，此刻CSB和DSC右半部分的正常作业。
DSC发生的斜坡需求经过比较器从头还原成矩形波。图1中的死区发生电路只能发生矩形波单侧死区时刻，而完好的死区功用需求由两个相同的如图1所示的结构组成。两个死区发生电路的DSC中相同端口连在一起，输入矩形波经过反相器把原输入信号和经过反相的输入信号别离输入Vin1和Vin2端口，经过处理的输入矩形波就发生带有死区时刻的反相的驱动类型。
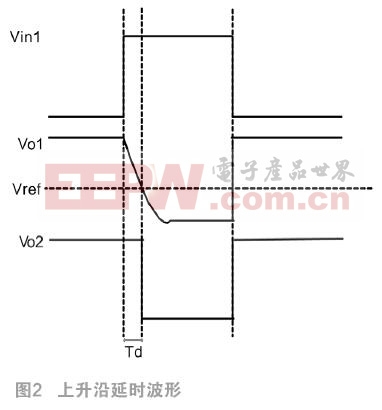
以图1中DSC斜坡发生电路左面部分为例， 图1中DSC的Vin1和Vin2是输入需求延时的矩形波信号，Vc1和Vc2是死区时刻操控端，经过操控充放电电流来操控延时。因为晶体管M1c的宽长较大，所以当Vin1下降沿时输出电压Vo1简直瞬间上升到电源电压VDD简直没有延时，但放电电流遭到Vc1操控，放电电流受限，因而会发生一个电压斜坡。因为输出点Vo的寄生电容是多个MOS管寄生电容的和，其值等于
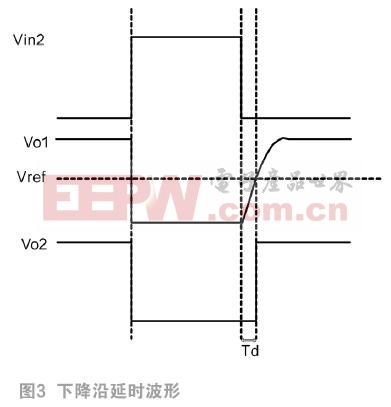
CT=Cds1c+Cgd1c+Cds3c+Cgd3c+Cds4c+Cgd4c+Cds6c+Cgd6c，其间还包含比较器的输入电容，但因为其电容值较低，因而疏忽。并且因为晶体管M1c、M3c、M4c、M6c的尺度较大，因而其寄生电容的值也比较大，可调的死区时刻规模二百多纳秒。当Vsel为高电平左边部分正常作业时， Vc1操控寄生电容C_T的放电电流，发生电压斜坡的斜坡在放电初始阶段的斜率是固定的，其斜率为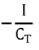
(I为初始放电电流)。将该斜坡电压与一个固定电压比较较就发生使矩形波单侧延时时刻，如图2所示。输入矩形波Vin1的下降沿到输出矩形波Vo2的下降沿之间的时刻距离便是延时时刻Td，也便是死区时刻。同理，斜坡发生电路右边部分电路能够使下降沿延时，如图3所示。
1.1 电路的功能剖析
为了核算死区时刻，即延时时刻Td。本文以下降沿延时电路为例。设比较器的参阅电压为Vref ，当输入矩形波Vin1下降沿时，寄生电容CT被敏捷充电到电源电压VDD，即Vo1敏捷上升到VDD，输入矩形波Vin1下降沿与Vo2上升沿时刻距离太短能够疏忽。当输入矩形波Vin1上升沿时，给寄生电容CT充电的M1c晶体管处于封闭状况，可是因为放电晶体管M5c受操控电压Vc1操控翻开，寄生电容C上的电荷被缓慢开释。
Q=C(VDD-Vref )=ITd (1)
其间，I为M5c的漏级放电电流，M5c的作业状况跟着输出电压Vo1的改动而改动。假定输出电压Vo1的初始电压为VDD，M5c的操控电压为Vc1，此刻M5c作业在饱满区，M5c开端给寄生电容CT放电。若疏忽沟道长度调制效应，放电电流I为固定电流。当输出电压Vo1-Vds3c﹤Vc1-VT时，M5c进入线性区，此刻的放电电流并不是一个固定值，而是跟着输出电压Vo1改动。可是在图1的死区发生电路中延时电压Td与比较器参阅电压相关，延时过程中M5c的作业状况也与比较器的参阅电压相关。当比较器参阅电压时Vref-Vds3c ≥Vc1-VT，那么寄生电容CT的放电电流是一个仅受操控电压Vc1操控的值。当Vref-Vds3c<vc1-vt时，寄生电容ct的放电电流一起遭到操控电压vc1操控和vo1电压影响。这儿核算设比较器参阅电压vref-vds3c p="" ≥vc1-vt，那么m5c的放电电流只受vc1操控，mos管电流和电压满意平方律联系：
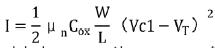(2)
其间，μn为NMOS管的迁移率， Cox为NMOS管的栅氧化层电容，W为NMOS管的栅极宽度，L为NMOS管栅长，VT为NMOS管阈值。
即：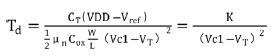
(3)
其间，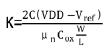
为常数，从上述公式能够看出，延时时刻Td与操控电压Vc1是负幂指数联系并不是线性联系。非线性联系会对死区时刻操控发生负面影响，如在某些电压规模内，死区时刻随操控电压剧烈动摇，无法得到要求的参数。为了校对死区时刻 Td与操控电压Vc1的非线性，图1中的死区发生电路添加了CSA和CSB部分。以CSA为例，该部分电路由电阻R1a和MOS管M1a组成。此刻的死区时刻为：
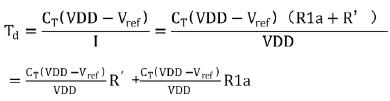(4)
其间， R' 为二极管衔接的M1a的输出电阻。该电阻值并非定值，可是因为其值较小，动摇起伏小，能够视为定值。从式(4)可知，MOS管M1a和M5c组成的电流镜结构把操控端由电压转化成了电流，一起把死区时刻Td与操控电压Vc1的负二次幂联系转化成了死区时刻Td与操控电流的负一次幂联系。此刻只要使M1a的电流I与某个量成反比例联系，就能把死区时刻与该变量转化成线性联系。而欧姆定律刚好满意反比例联系，因而得到(4)。从(4)中能够知道死区时刻Td与外接电阻R1a成线性联系，可是该曲线不经过坐标原点，因而它有最小的死区时刻为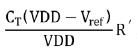
，即当R1a为零的时分。当Vsel为低电平时，下降沿延时电路和DSC正常作业，其成果相似于上升沿延时电路。
2 仿真成果
根据0.5 μm的BCD工艺，对提出的死区发生电路进行仿真。规划选用的供电电压为5 V，输入的方波占空比为50%，作业频率为500 kHz。为了比较电阻操控死区发生电路和电压操控死区发生电路，对电压操控的死区发生电路也进行了仿真。这儿比较器参阅电压为2.6 V。
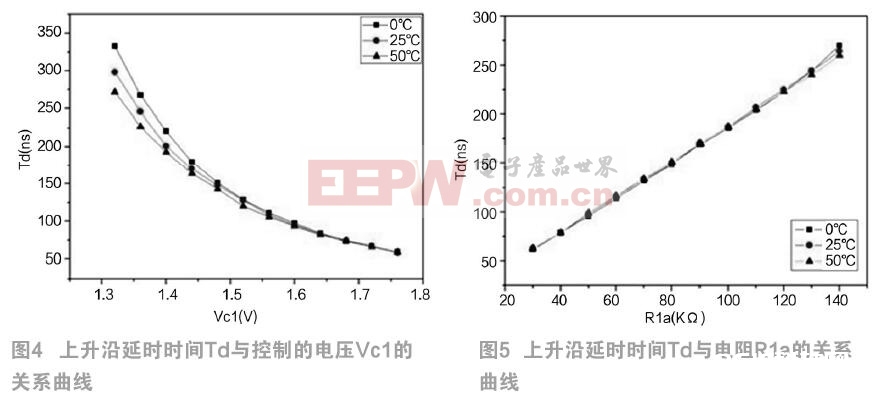
经过对电路进行瞬态仿真，扫描不同操控电压下，不同电阻下的死区时刻别离得到死区时刻Td随操控电压和电阻的联系曲线，一起还扫描在0 ℃、25 ℃、50 ℃下的特性曲线。图4所示为不同温度下的上升沿死区时刻Td与操控的电压Vc1的联系曲线，从图4中可知，上升沿死区时刻Td与操控的电压Vc1的联系曲线正如公式(3)剖析的那样，死区时刻Td与操控电压Vc1是负二次幂联系，跟着Vc1的添加，死区时刻的斜率绝对值逐步减小。在操控电压Vc1逐步增大时，延时时刻Td逐步减小，因为跟着操控电压Vc1增大，寄生电容CT的放电电流增大，电压下降更快，延时时刻Td减小。此外，温度对延时时刻Td有影响，跟着温度的升高，延时时刻Td减小。并且，在放电电流较小时温度对放电电流会发生严重影响，这导致死区时刻的精确度下降。图5是不同温度下的上升沿延时时刻Td与电阻R1a的联系曲线， 与图4比较，上升沿死区时刻Td与外接电阻是呈线性改动的，25 ℃条件上升沿延时时刻Td与电阻R1a的联系式为 Td=1.8R1a+6，死区时刻 Td在0～50 ℃相对误差3%以内。并且从图5中可知，三条温度曲线重合程度十分高，这能够阐明温度对死区时刻的影响较小。
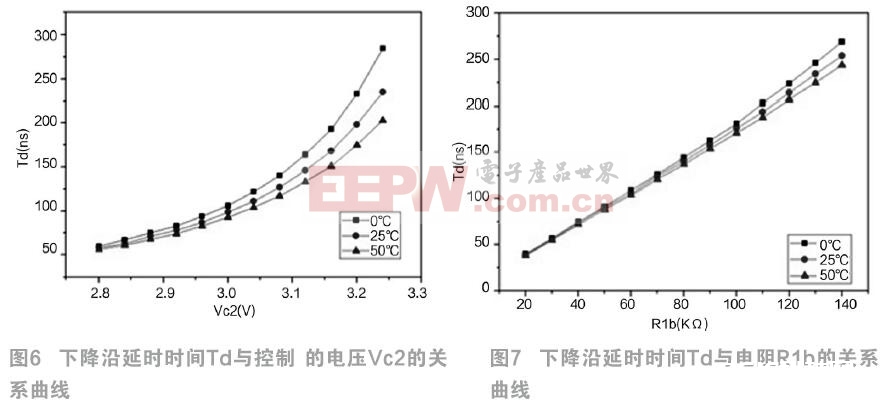
同理，当Vsel输入低电平时，下降沿死区发生电路正常作业。下降沿延时时刻Td与操控电压Vc2和外接电阻R1b的联系如图6和图7所示。下降沿死区发生电路的作业原理与上升沿死区发生电路相似，可是下降沿死区发生电路相对于上升沿死区发生电路对温度更灵敏，这或许是因为NMOS管对温度更灵敏形成的。 25 ℃条件下延时时刻Td与电阻R1b的联系式为Td=1.8R1b+1，延时时刻Td在0-50℃相对误差在6%以内。相对于上升沿延时，下降沿延时精确度更低一些。
相较与典型的死区发生电路[5]，本文提出的死区发生电路改动死区时刻的发生方法，电路结构更简练、紧凑，并且死区发生电路包含了典型死区发生电路中的驱动电路。此外，把本来固定不可调死区发生电路调整为死区时刻线性可调，极大地增强了电路的功能。
3 定论
本文规划了一种新式的线性可调死区电路，该电路经过改动电压斜坡的斜率来来调整死区时刻。本文规划的固定死区发生电路结构简练，经过批改电压对死区时刻的非线性，终究获得了高精度线性可调的死区时刻，比较典型的死区发生电路具有更广泛使用。
参阅文献：
[1] Romain Grezaud,Francois Ayel , Nicolas Rouger,et al. A Gate Driver With Integrated Dead-time Controller[J]. IEEE TRANSSACTIONS ON POWER ELECERONICS, VOL. 31, NO. 12, DECEMBER 2016, pp.8409-8421.
[2] Vahid Yousefzadeh, Dragan Maksimovic . Sensorless optimization of dead times in DC-DC convertors With synchronous rectifiers, IEEE Trans Power Electron., vol.21, no. 4,pp.994-1002,Jul. 2006.
[3]刘飞云.有源钳位正激变换器的研讨[D].武汉:华中科技大学,2004.
[4] CHRISTOPHE P. BASSO, SWITCH-MODE POWER SUPPLIES [M]. MCGRAWHILL PRESS, 2008.
[5] SeongWha Hong, Hong-Jin Kim and Kang-Yoon Lee, et al. A Novel Dead-time Generation Method of Clock generator for Resonant Power Transfer System [C] // SOC Design Conference (ISOCC), 2010 International, South Korea. 2010: 51-54.
本文来源于《电子产品世界》2018年第9期第71页，欢迎您写论文时引证，并注明出处。
