在计数体系中,通常用的是十进制,它有0,1,2,3,…,9十个数码,用它们来组成一个数。但在数字电路中,为了把电路的两个状况(1态和0态)和数码对应起来,选用二进制较为便利,二进制只要0和1两个数码。

二进制加法器是数字电路的根本部件之一。二进制加法运算同逻辑加法运算的意义是不同的。前者是数的运算,而后者表明逻辑关系。二进制加法是“逢二进一”,即1+1=10,而逻辑加则为1+1=1。
1、半加器
所谓“半加”,便是只求本位的和,暂不论低位送来的进位数。半加器的逻辑状况表见表1。

表1半加器逻辑状况表
其间,A和B是相加的两个数,S是半加和数,C是进位数。
由逻辑状况表可写出逻辑式:
并由此画出图1(a)的逻辑图。图1(b)是半加器的逻辑符号。
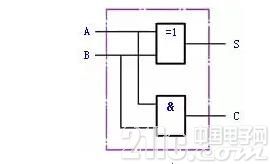
(a)逻辑图
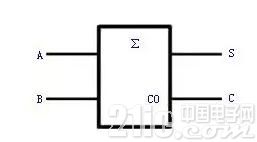
(b)逻辑符号
图1半加器逻辑图及其逻辑符号
2、全加器
当多位数相加时,半加器可用于最低位求和,并给出进位数。第二位的相加有两个待加数,还有一个来自低位送来的进位数。这三个数相加,得出本位和数(全加和数)和进位数,这便是“全加”,表2是全加器的逻辑状况表
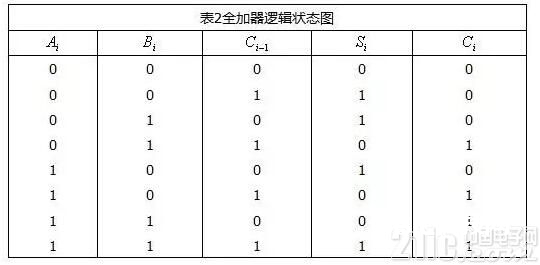
全加器可用两个半加器和一个或门组成,如图2(a)所示。在第一个半加器中相加,得出的成果再和在第二个半加器中相加,即得出全加和。两个半加器的进位数经过或门输出作为本位的进位数。图2(b)是全加器的逻辑符号。
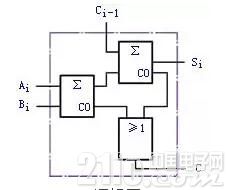
(a)逻辑图
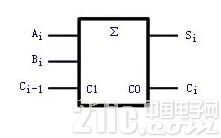
(b)逻辑符号
图2 全加器逻辑图及其逻辑符号
例1、用4个全加器组成一个逻辑电路以完结两个4位的二进制数A—1101(十进制为13)和B—1011(十进制为11)的加法运算。
解:
逻辑电路如图3所示,和数是S—11000(十进制数为24)。依据全加器的逻辑状况表自行剖析。
这种全加器的恣意一位的加法运算,都必须比及低位加法完结送来进位时才干进行。这种进位方法称为串行进位,它的缺陷是运算速度慢,但其电路比较简单,因而在对运算速度要求不高的设备中,仍不失为一种可取的全加器。T692集成加法器便是这种串行加法器。
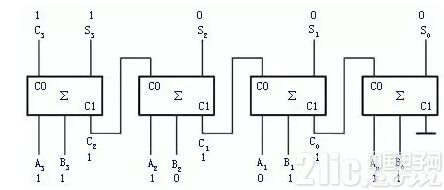
图3 例1的逻辑图