针对在导航体系姿势解算中,陀螺仪和电子罗盘在解算姿势时别离存在积分差错和磁场搅扰的问题,提出了使用Kalman滤波和互补滤波相交融的算法进行定位。首要将电子罗盘和陀螺仪经过Kalman滤波得出最优估量四元数,然后使用互补滤波算法对陀螺仪的漂移进行补偿得到校对后的四元数,将此次得到的四元数和Kalman滤波得出最优估量四元数再次经过Kalman滤波对四元数进行第2次最优估量,从而输出姿势角。试验中比照了本算法和互补滤波算法、无滤波算法的作用。试验证明,该算法不只可以有用处理方位角差错发散问题,还有用处理了磁场搅扰问题,完结了高精度的方位输出。
跟着以MEMS(Micro-electromechanical Systems)传感器为代表的微型化惯性器材的开展,根据捷联式惯导原理和MEMS传感器的惯性定位技能也日益遭到重视,特别是在难以接纳卫星信号的室内、地下、矿井、水下、战场等场合[1]。针对上述问题往往选用使用电子罗盘对陀螺进行校对的办法,在室内、地下、矿井、水下等过程中磁强计愈加简单遭到搅扰,形成方位更大的差错。针对磁强计易受搅扰和陀螺积分漂移的问题已经有很多交融的算法呈现,比方卡尔曼滤波、无迹卡尔曼滤波(UKF)、扩展卡尔曼滤波(EKF)等[2-4],这些滤波办法需求树立精确的状况方程和观测方程。还有一种滤波算法是在互补滤波的基础上进行扩展,比方经典互补滤波、根据梯度下降法的互补滤波算法等[3-6],可是这种滤波算法适用的精度不高。面临这些问题,本文提出了一种Kalman滤波和互补滤波交融的惯性定位算法,该算法在规划Kalman滤波中,将加速度计和磁强计交融得出的四元数作为观测值,使用陀螺仪得出的四元数作为状况值,经过数据的交融进行滤波,完结四元数的第一次最优估量,针对陀螺漂移问题则使用所规划的互补滤波对陀螺漂移进行补偿,得到校对后的角速度,从而求得校对后不断更新的四元数,然后和第一次完结的最优估量四元数经过第2次Kalman滤波进行估量,从而输出高精度的姿势角。
1 算法整体规划
Kalman滤波和互补滤波交融的惯性定位算法的整体思路如图1所示。
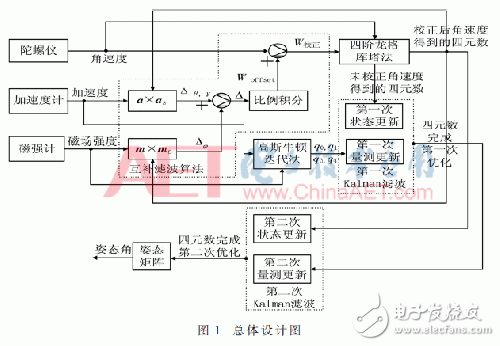
首要,将磁强计和加速度计丈量的磁场强度和加速度使用高斯牛顿迭代法解算出的四元数送入Kalman滤波中当作观测值,将陀螺仪丈量的角速度值使用四阶-库塔法解算出的四元数作为Kalman滤波的状况值从而得到四元数的第一次最优估量值,在Kalman滤波过程中既可以去掉随机噪声,经过电子罗盘对陀螺仪进行校对,又可以防止因为磁场搅扰带来的搅扰数据。
其次,使用载体坐标系和地舆坐标系之间的转化矩阵,将地舆坐标系下的重力和地磁重量转化到载体坐标系下,然后与加速度计和磁强计在载体坐标系下丈量得到的加速度和磁场强度做向量积的运算,将二者向量积的和相加经过份额积分低通滤波,可以将电子罗盘丈量姿势中的高频颤动信号滤出,然后和陀螺仪丈量的角速度进行交融,得到对陀螺仪补偿后的角速度,使用四阶龙格库塔法得到校对后的四元数。
最终,将互补滤波算法得到的校对四元数作为状况量,将第一次Kalman滤波得到的最优四元数作为观丈量进行第2次Kalman滤波,完结四元数的第2次优化,然后经过四元数树立姿势矩阵求得愈加精确的姿势角。
2 卡尔曼滤波规划
卡尔曼滤波(Kalman filtering)是一种使用线性体系状况方程,经过体系输入输出观测数据,对体系状况进行最优估量的算法。树立体系的状况方程和丈量方程是卡尔曼滤波的首要作业。本次卡尔曼滤波规划顶用四元数的不断更新量作为卡尔曼滤波中的状况量。

下面树立丈量方程,由重力加速度和三轴加速度计

式(4)中ax、ay、az表明重力加速度的丈量值,重力加速度用g表明。
由地磁场和磁强计丈量信息之间的联系可得:

由式(6)、式(7)并经过高斯牛顿迭代法求得四元数,作为观丈量。观丈量取为:

式(8)中观丈量方程Z(k)=H(k)X(k)+V(k),其间H(k)为观丈量的增益矩阵,V(k)为观测噪声,方差R(k)可以经过传感器的丈量数据取得。因为第一次Kalman滤波和第2次Kalman滤波都是对四元数的最优估量,故上述滤波公式和树立的方程均坚持不变。
3 互补滤波算法规划
因为陀螺仪经过积分得到的方位角存在长期差错积问题,但其动态呼应好,不易受外界搅扰,而与之对应的电子罗盘易受外界搅扰,但它具有无差错累积的长处。互补滤波便是使用陀螺仪的高频特性和电子罗盘的低频特性进行交融,经过份额环节进行频率特性的调理,如图2所示。
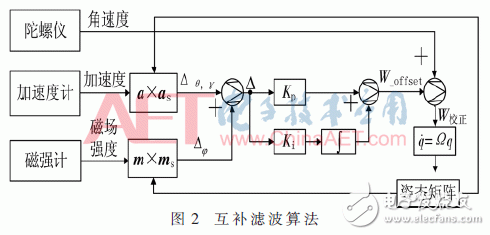
在图2中,a、m表明载体坐标系下加速度计和磁强计丈量得到的加速度和磁场强度;将地舆坐标系下的重力重量和地磁重量经过四元数构成的姿势转化矩阵变换为载体坐标系下的重力重量和地磁重量,别离用as和ms表明。在载体坐标系下别离对a、as和m、ms做向量积的运算,得到加速度计和磁强计对陀螺仪的校对差错。其间俯仰角和横滚角的差错设为Δθ,γ,航偏角的差错设为ck5-gs8-x1.gif即:

将最终得到的角速度经过四阶龙哥库塔法进行姿势解算,得到最优姿势角。
4 试验验证和成果剖析
本文选用MPU9150模块进行试验验证,经过硬件I2C总线的办法进行数据的读取,传感器按100 Hz/s进行数据更新,以外部中止的办法进行数据收集,然后将收集的数据存放于TF中,经过MATLAB编程进行数据调用。为了验证此惯性定位交融算法的作用,首要在行走和磁场搅扰严峻的两种形式下进行测验,且两种办法都是在室内完结。图3为带着传感器人员(将传感器绑在脚上)在室内某一方位动身,转一圈回到开始方位,时长约5 min;图4为带着传感器人员鄙人电梯过程中坚持站立姿势的测验。在图3和图4中,单个陀螺仪解算(无滤波算法)用图(a)代表,互补滤波算法用图(b)代表,本算法用图(c)表明。
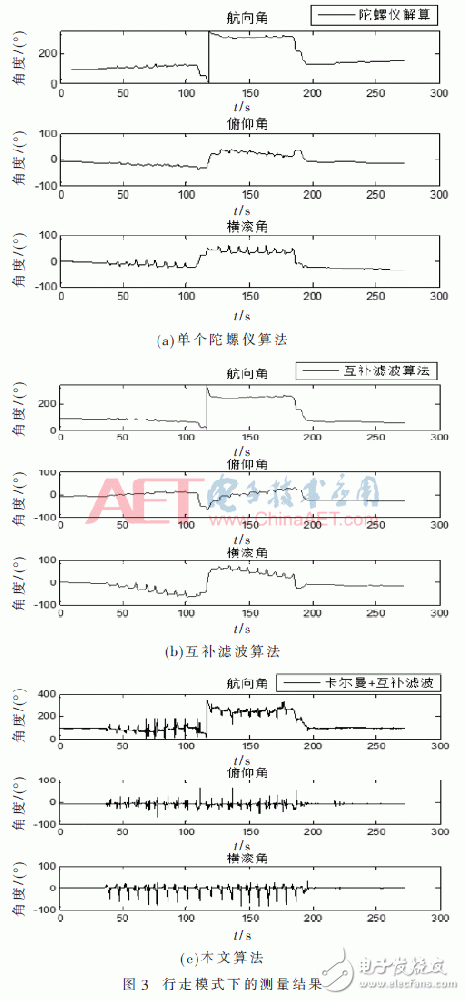
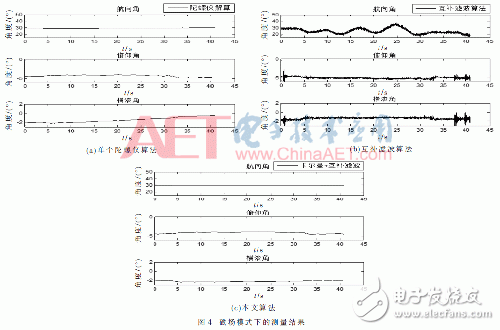
经过图3比照始末方位方位差错的数据成果可知,互补滤波算法尽管比单个陀螺进行行人方位解算愈加精确,可是使用互补滤波算法始末方位差错在8°之内,而本算法在行走5 min左右始末方位差错在 1.5°之内。由图3(c)证明本算法可以精确提供在大动态下(转圈)的方位。由图4可知,在电梯内磁强计遭到激烈搅扰的情况下,仅使用互补滤波算法会比单个陀螺进行解算呈现更严峻的方位差错问题,而使用Kalman滤波和互补滤波相交融的惯性定位算法防止了此问题,保证姿势精度在2°以内,有用按捺了磁场强度的搅扰,保证方位的高精度输出。
5 结束语
本文针对在导航解算中陀螺仪的积分差错和磁强计简单遭到搅扰的问题,提出了一种使用Kalman滤波和互补滤波相交融的惯性定位算法,使用Kalman滤波求最优四元数,使用互补滤波对陀螺仪的角速度进行校对,经过校对的角速度进行四元数的更新,将两次校对后的四元数经过Kalman滤波求最优四元数。经过试验成果可以看出,此办法不只可以很好地处理陀螺漂移问题,还能有用按捺磁强计遭到搅扰的问题,可以精确地对方位进行校准,完结姿势角高精度的安稳输出。