文章转自ADI官网,版权归属原作者一切
倾角丈量的典型运用
本文旨在评论如何用组合器材一类的加速度计进步倾角丈量的精度。在乘用车上,电动驻车制动器(EPB)被用于使轿车在平整的分级路途上坚持停止。这是经过用一个单轴或双轴加速度计丈量倾角来完成的。一般做法是将一个X轴/Y轴或Z轴低g加速度计装在EPB操控单元中一个专门的模块中。现在,越来越多的轿车配有ESC(电子安稳操控)功用,在单个芯片中集成了组合式低g加速度计和陀螺仪。这样做是为了避免轿车侧滑和翻车;现在,ESC功用现已成为国际各国或区域法令的强制要求。假定经过组合器材(单芯片、组合式加速度计和陀螺仪)完成倾角丈量,则不用在车上装置一个独立的EPB模块,成果能够大幅下降轿车的本钱。因为组合器材一般用于ESC,所以并未针对倾角检测优化,而且经过组合器材丈量倾角时,丈量精度有时无法到达要求。因为组合器材是XY轴或XYZ轴,所以一般用X轴进行倾角丈量,EPB模块中的部分传统型低-g加速度计运用的是Z轴,因为它是笔直装置在发动机舱里的。检测轴应该与重力笔直,才干取得更高的精度——咱们稍后会评论这一点。
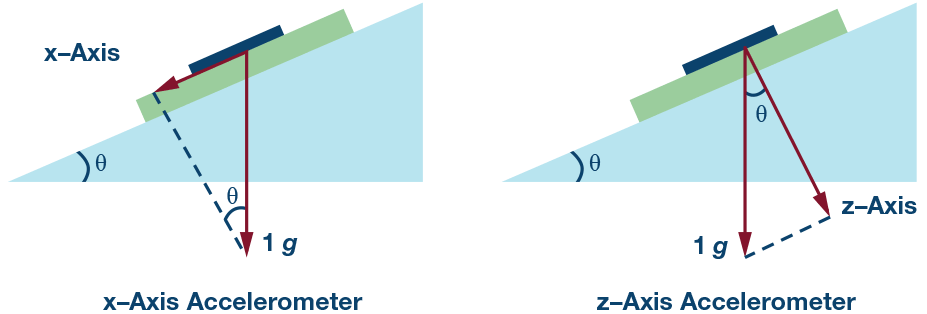
图1. X轴和Z轴加速度计的装置示意图。
关于轿车中的倾角丈量,评价精度对错常重要的。无妨想像,您的车停在肯定平整的地上,因而,加速度计核算的倾角应该是0°。假定您的车停在斜坡上,就应该精确地检测出倾角,以便正确地激活刹车体系。
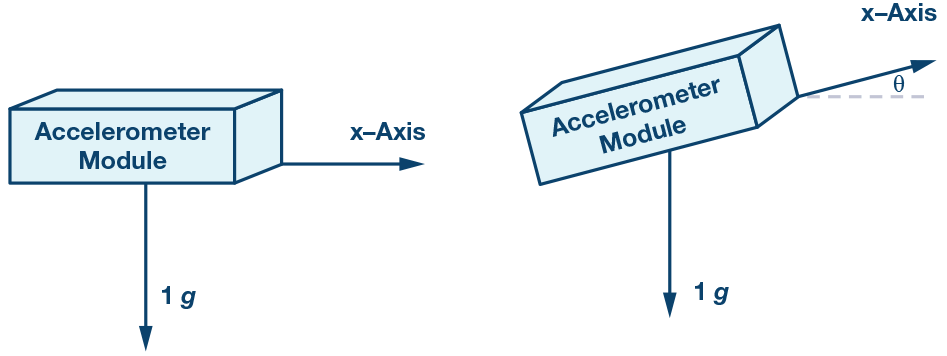
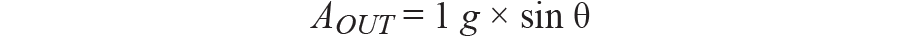
因而
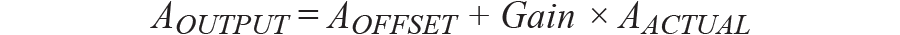
其间:
AOUT 为加速度计的输出,单位为g。
θ 为斜坡的倾角,单位为度。
因为sin θ是一个非线性函数,所以,AOUT与θ之间的联系对错线性的,在挨近零时其线性度处于最佳状况,即其此刻具有最佳的丈量精度。跟着θ的增大,丈量精度下降。这正是检测轴应与重力笔直的原因,因为路途斜度将挨近零
关于轿车倾角丈量,不用在全斜坡斜度的条件下考虑体系。实践国际中,路途上的绝大大都斜坡斜度不会超越30°。咱们只需求剖析在±30°的规模内剖析奉献要素的精度即可。
影响体系级丈量精度的奉献要素有多个:
- 灵敏度差错和初始肯定失调
- 非线性度
- 与初始肯定失调的总失调改变
- 噪声
灵敏度差错和初始肯定失调
灵敏度差错
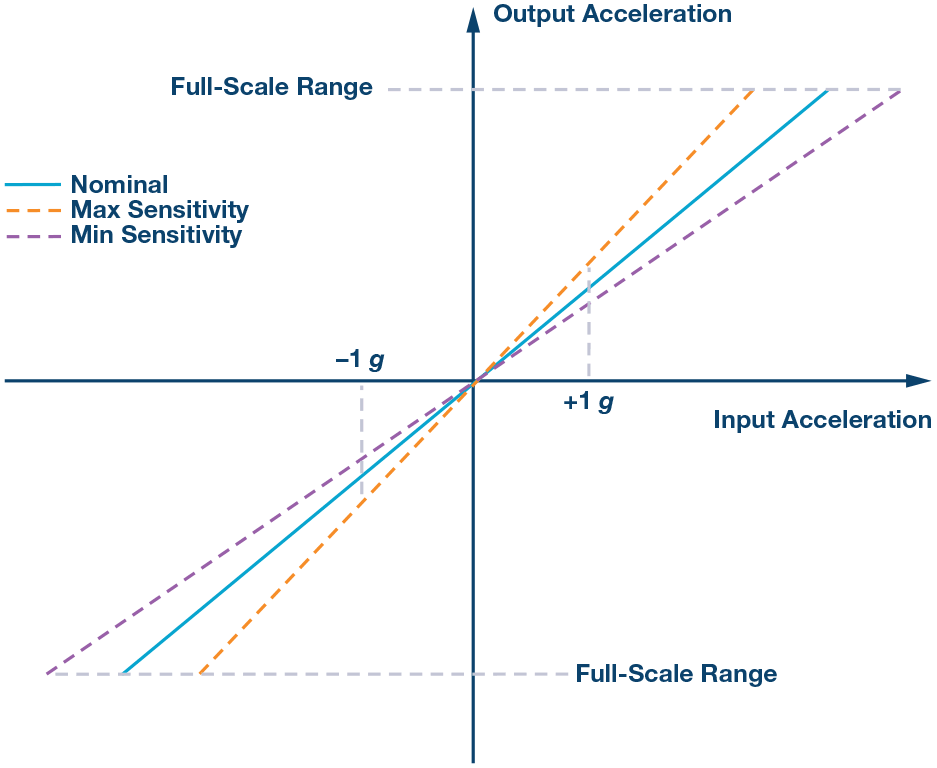
灵敏度是对输入-输出测得的传递函数的斜率,一般为+1g和–1g。灵敏度差错为器材间的灵敏度差错。例如,有些加速度计的最大灵敏度为3%。

初始肯定失调
规模内的失调约为25°C;例如,在模块制作完成后当即丈量的值为25°C ± 5°C。初始肯定失调表明很多器材的实测偏移值的标准差。
两点校准
关于倾角丈量运用,两个首要的差错来自失调差错和灵敏度差错。这两种差错会导致不行承受的检测成果,因而不得疏忽。假定咱们期望消除这些部分差错,则应对加速度输出进行校准。一般地,要对倾角丈量的失谐和灵敏度进行一次校准。若要考虑失谐和灵敏度差错,则加速度计输入与输出的联系为:
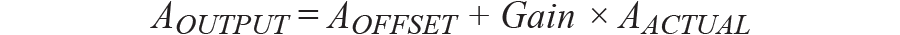
其间:
A输出 为失调差错,单位为g。
增益为加速度计的增益,抱负值为1。
A实践为施加于加速度计的实践加速度,单位为g。
有两种根本校准技能;其间一种是单点校准。这种校准的具体做法是在加速度计上施加一个0g场,然后丈量输出。这类校准只能用于校准失调差错,不能校准增益差错。然后,从实践输出值中减去0g场里的输出成果,消除失调差错。这种校准办法十分简略,但精度缺乏,因为依然存在灵敏度差错。另一种办法是1g翻转校准,在+1g和–1g时选用两点校准,并在每个+1g和–1g场内依照以下公式丈量加速度输出:
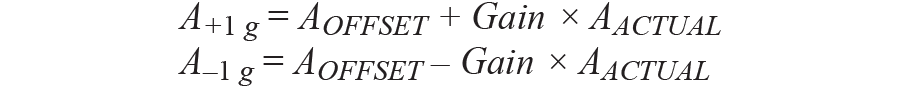
其间,失调A失调的单位为g。
以这两点信息为根底,能够依照以下办法解出失谐和增益:
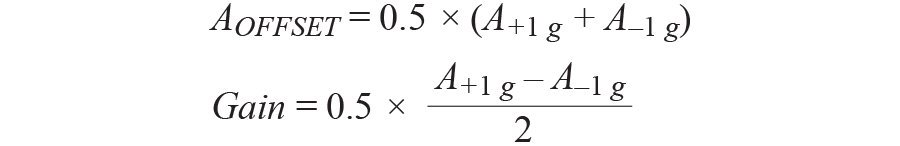
其间,+1g和 1g丈量值、A+1g和A–1g均以g为单位。
经过这一次校准今后,能够用该等式核算实践加速度,每次都会消除失调差错和灵敏度差错。
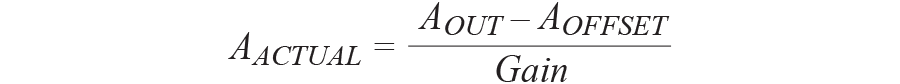
其间,A失调和A输出以g为单位。
非线性度
器材的非线性度为测得加速度(AMEA)与抱负线性输出加速度(AFIT)之间的最大差错。加速度丈量数据集应包含加速度计的满量程规模。其丈量办法为Max(|AMEA – AFIT|)。
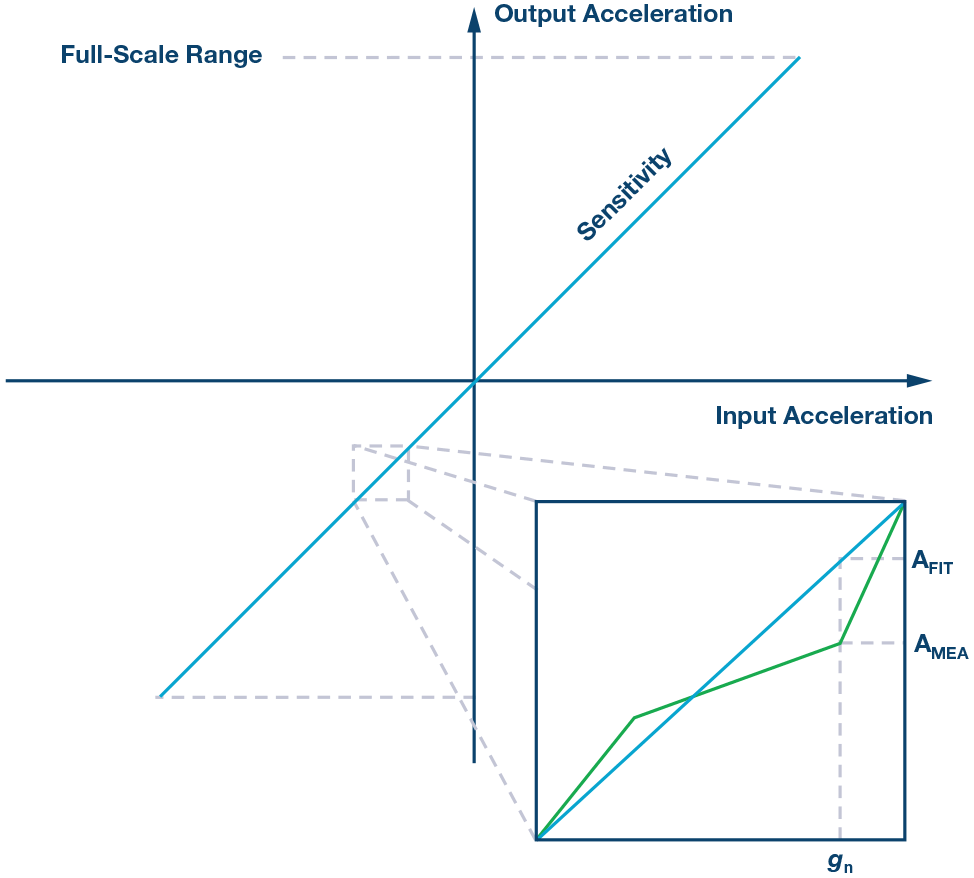
其间:
AMEA为给定gn下的测得加速度。
AFIT 为给定gn下的猜测加速度。
大都加速度计或组合器材在给定输入加速度计规模内均存在非线性——例如,30 mg ± 2g的规模。关于倾角丈量运用,输入坡道斜率在±30°以内,这意味着输出加速度规模在±500 mg (±1g× sin 30°)以内,所以应从头评价该规模内的非线性度。因为非线性度在整个输入规模内对错线性的,所以,很难精确地量化评价这部分差错。但是,因为该器材的数据手册一般都很保存,线性度为30 mg,输入规模为±2g,用10 mg核算±500 mg规模内的差错更合理些。
与初始肯定失调的总失调改变
与初始肯定失调的总失调改变为温度、应力和老化效应导致的失调的最大差错。该差错是相关于给定器材的初始肯定失调进行丈量的。这是精度总差错的首要奉献要素。
在温度、应力、老化等一切这些要素中,改变与温度在总失调改变中占比很大。一般地,改变与温度曲线是二阶曲线,一般为旋转抛物线。为了消除这部分差错,能够在体系级履行三点校准。关于给定器材,可按下列过程校准输出失调随温度的改变值。
第1步:
使器材的输出响应以某个 ∆N0值偏移。温度校准流程的第一步是消除环境温度下的失调。
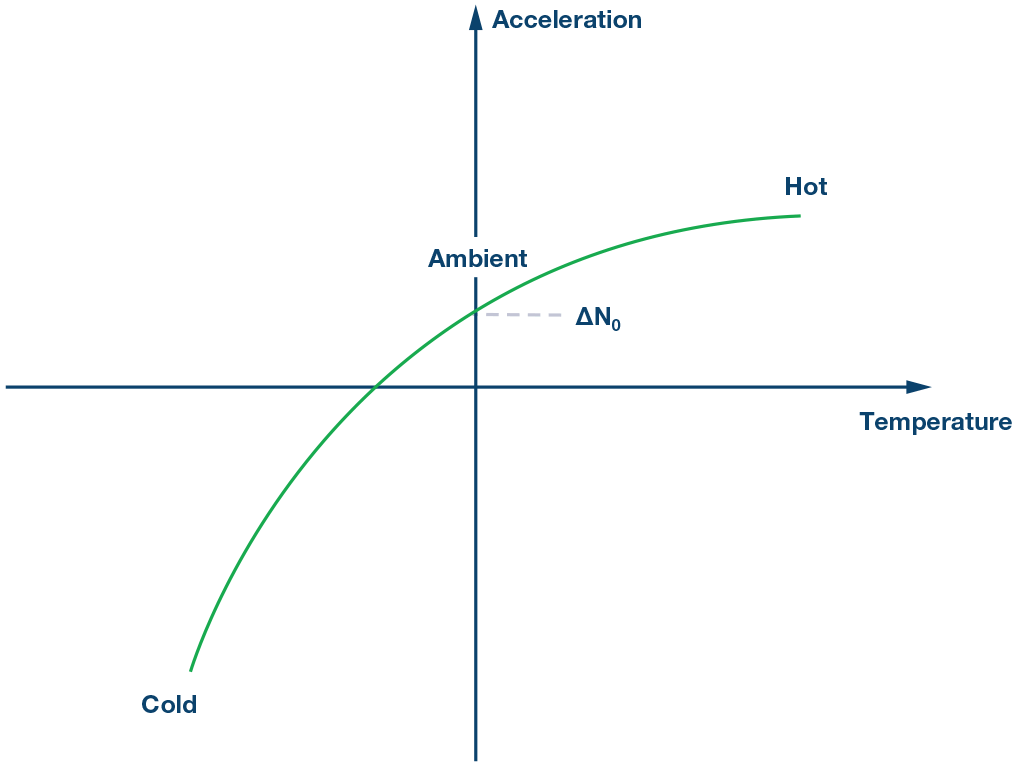
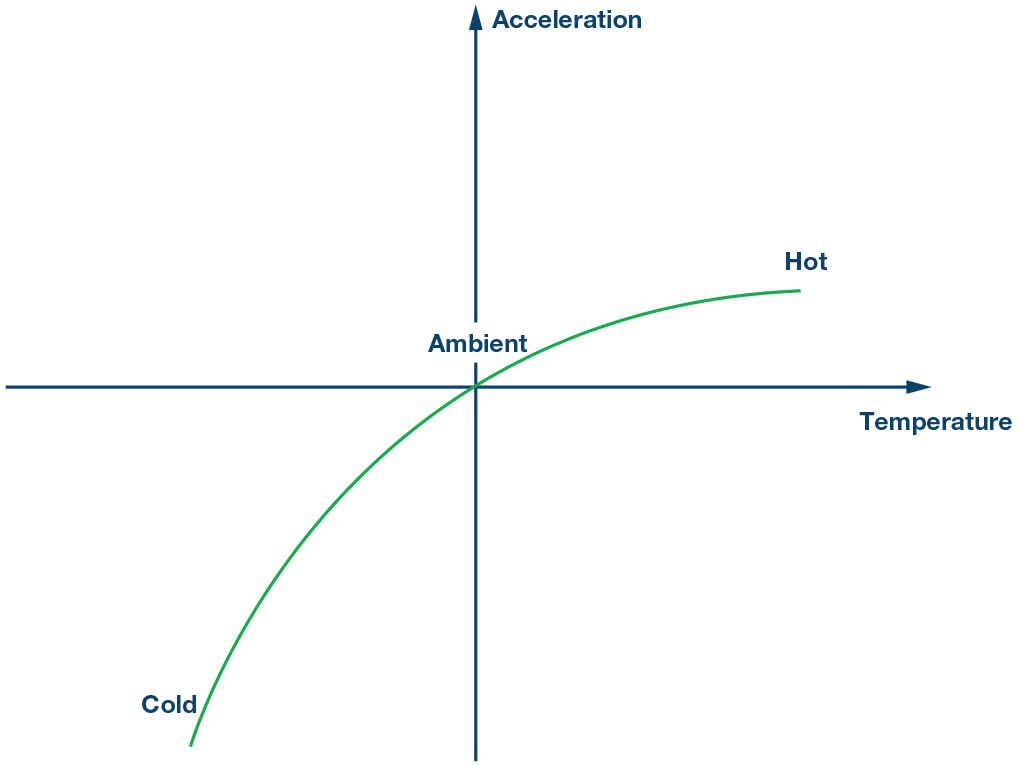
第2步:
接下来,在高温下测验器材,用取得的新信息生成失调校对线性公式。
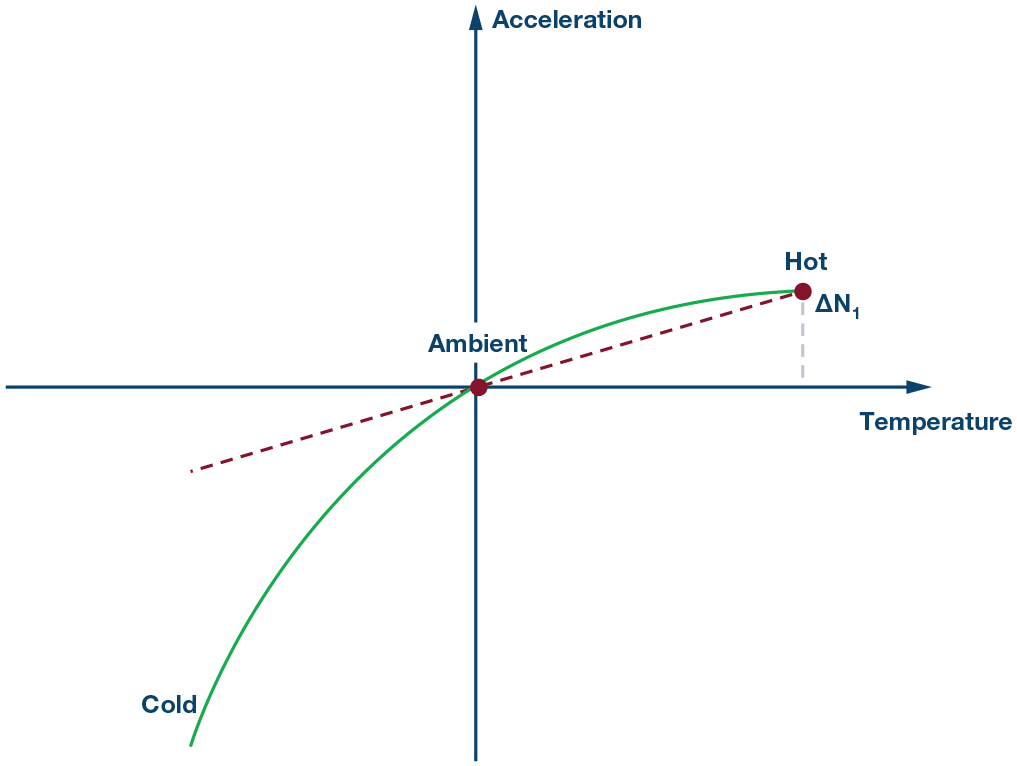
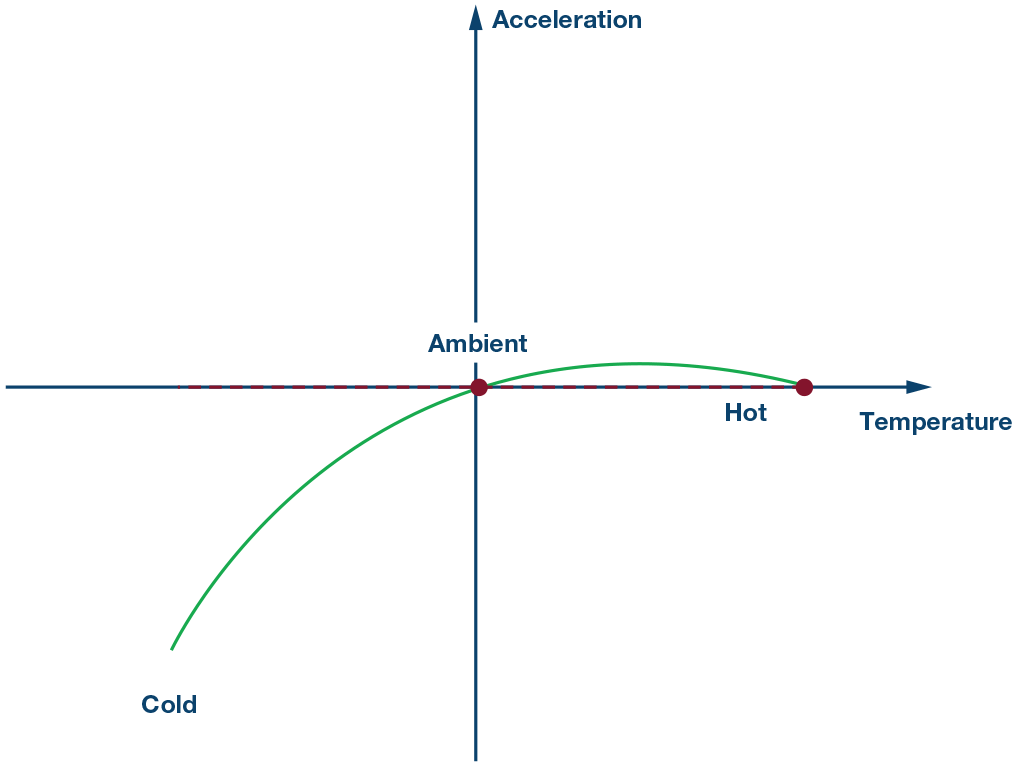
第3步:
给现有公式增加一个二阶重量,校对失调剩下部分。设二阶曲线遵从以下公式:
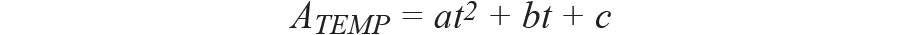
这是二阶抛物线公式,现已经过第1步和第2步消除了旋转重量。
在该公式中,该二阶抛物线有三个解:
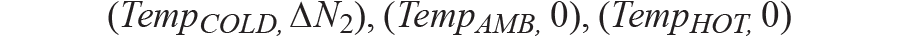
然后,咱们能够得到温度系数 a, b, c.
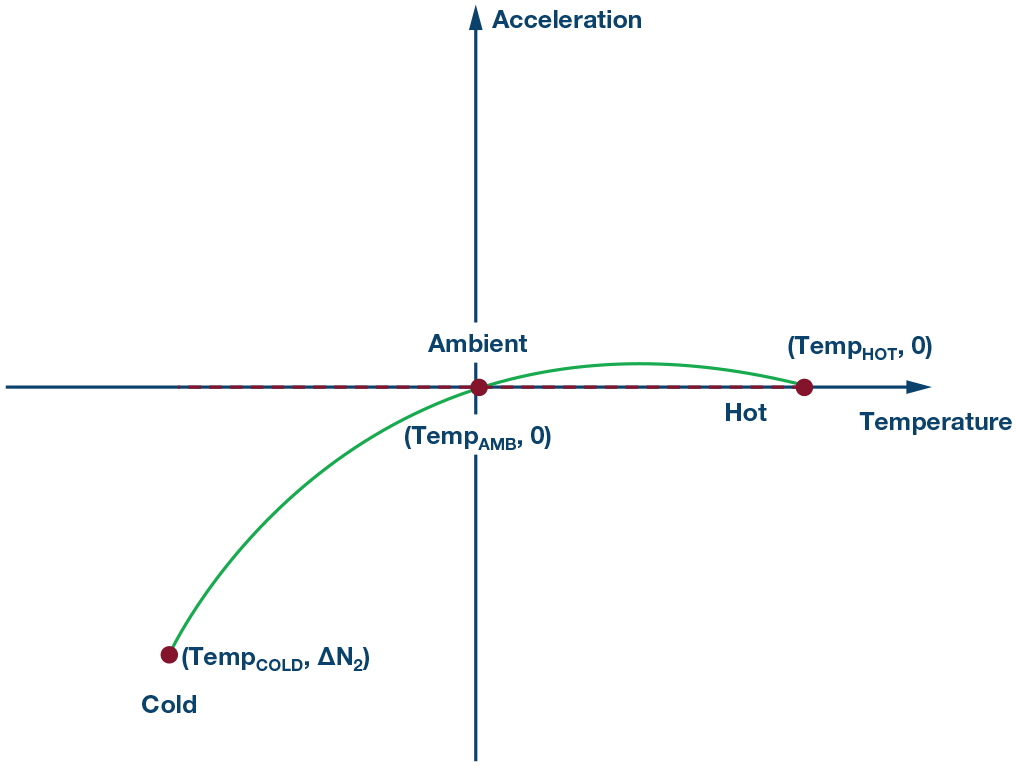
有关∆N0, ∆N1, ∆N2, a, b, c 的一切温度系数信息应该存储在体系非易失性存储器中,一起需求一个板载温度传感器。体系会在每次上电后例行校准加速度计,保证消除失调随温度的改变值。
噪声
根据单个数据样本丈量倾角不一定牢靠。即便加速度计的噪声为零,倾角丈量也是在轿车启动时丈量的,所以,需求减小发动机、过往车辆或乘客在车上来回移动导致的任何振荡。最好的办法是在不降至最低数据速率要求的条件下,在尽量长的时间内做数据均匀。数据均匀算法会削减rms噪声。
假定咱们对噪声采样,成果可得到每个样本的方差
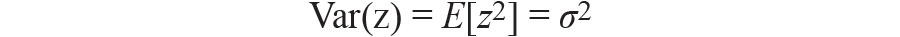
求一个随机变量的均值,取得以下方差,
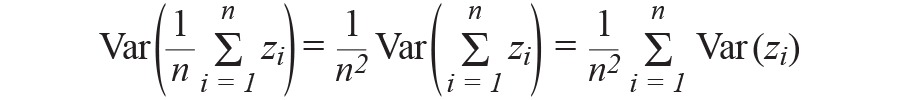
因为噪声方差坚持于σ2不变,
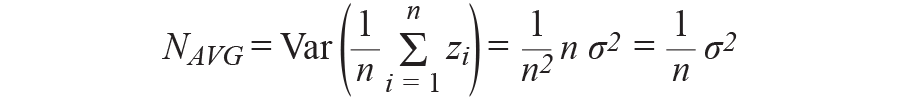
以上推导显现,对同一未校对噪声的n次完成求均值可使噪声功率削减n倍,并使rms噪声削减√n。
因为随机噪声受高斯散布影响,所以,rms噪声等于高斯散布的标准差。6σ以内的最小散布为97%。
例如,假定以1 kSPS的采样率对每100 ms的数据求均值,则最大rms噪声 = 0.4 mg,便是说假定以6σ作为与均匀值的间隔,则此刻的峰值噪声仅为2.4 mg。
用于与rms值相乘的因数取决于器材要履行的使命的计算需求。例如,假定挑选6作为因数(峰峰值噪声为6 × RMS_Noise),则算法在器材生命周期内要运转的次数会影响超越最差状况6 × RMS_Noise 的概率。可总结如下:
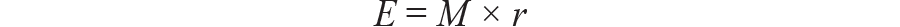
E为在生命周期内超越最差状况的预期次数,M为生命周期内的运转次数,r为超越最差状况的概率。根据此,咱们能够经过乘以rms噪声评价出一个合理的因数。
小结
以ADI公司的ADXC1500/ADXC1501(组合式陀螺仪和2轴/3轴加速度计)为例,一切差错奉献项均列于表1中,包含校准和不校准两种状况。咱们能够假定,总失调改变为二次曲线,而且其在温度规模内的改变占总失调改变的80%。别的,以6为因数乘以最大rms噪声。
一个陀螺仪和一个三轴加速度计的单芯片集成计划能够完成多种新式运用,尤其是在轿车安全体系和工业自动化运用领域。为了规划愈加牢靠、高精度的轿车安全体系,例如,安稳的电子操控体系(ESC)和侧翻检测体系,尽量削减体系差错至关重要。轿车中已装置这些传统型底盘操控体系,包含防抱死制动体系、牵引操控和偏航操控体系。
| 差错奉献 | 校准前 | 校准后 | 校准办法 |
| 灵敏度差错 | 30 mg | 0 mg | 两点校准 |
| 初始肯定失调 | 15 mg | 0 mg | 两点校准 |
| 非线性度 | 10 mg over ±500 mg | 10 mg over ±500 mg | 无 |
| 总失调改变 | 50 mg | 10 mg | 三点校准 |
| 噪声 | 24 mg | 2.4 mg | 100× 均值 |
| 总差错 | 129 mg | 22.4 mg | |
| 精度 | 7.4°(最差状况) | 1.28°(最差状况) | 单位:度 |
称谢
借此机会向我的两位搭档Matthew Hazel和Brian Larivee称谢,感谢他们在我编撰本文的过程中为我供给了许多启示。









