1 导言
现在,中高压变频器的产品中,电机调速操控战略多选用V/F操控或矢量操控(又称磁场定向操控),而直接转矩操控(Direct Torque Control,简称DTC)方面的研讨与运用较少,完成难度较大。主要原因之一在于多电平拓扑的开关管数目很多,形成传统DTC所需求的开关向量表非常杂乱。别的,传统DTC选用滞环比较器,逆变器开关频率不固定,难以数字完成,生成多电平波形较为困难,电流、转矩脉动较大。
完成DTC等高功能调速战略需求检测电机的转速,但速度传感器的装置添加了体系的杂乱性、本钱和保护要求,下降了可靠性和鲁棒性。
2 多电平直接转矩操控的难点
传统的直接转矩操控选用磁链与转矩的砰—砰操控,依据它们的改变与定子磁链地点的空间方位直接挑选电压空间矢量的开关状况,取得快速的转矩呼应[2]。可是其实践转矩在滞环比较器的上下限内脉动,开关频率也不固定。一种改善计划是将空间矢量调制(SVM)办法与DTC相组合,对转矩进行闭环PI调理,以电压空间矢量调制模块替代开关向量表,发生PWM波操控逆变器的开关状况,可使开关频率安稳,转矩脉动也大幅减小[3]。
但是,在多电平范畴,逆变器的根本空间矢量数目很多,关于每相n个H桥级联单元即 级级联的多电平逆变器,其根本空间矢量数目为(2n+1) 3个。每相3单元的高压变频器根本空间矢量多达343个,而关于每相6单元的高压变频器,这个数目到达了2197个。如此繁复的根本空间矢量使空间矢量挑选算法变得非常杂乱。别的,空间矢量的挑选要考虑功率单元的开关负荷均衡,这就对算法提出了更高的要求。因而,在电平数较多的情况下,空间矢量算法完成困难,也难以满意实时操控的要求[4]。
为战胜上述问题,在级联多电平中选用错时采样空间矢量调制(Sampe-Time-Staggered Space Vector Modulation,简称STS-SVM)战略,能大大下降空间矢量挑选的杂乱度,而且能够完成开关负荷的主动均衡,履行效率高,易于完成无速度传感器DTC等高功能实时操控。
3 错时采样SVM战略
图3 根据STS-SVM的无速度传感器DTC体系结构
4.1 STS-SVM调制的多电平逆变器
此处,多电平逆变器为图4(a)所示的三级H桥级联型拓扑。STS-SVM模型中的驱动信号的发生经过两电平空间矢量算法得出的调制波与各个开关管对应的三角波进行比较来取得,如图4(b)所示。各个三角载波存在必定的移相联系,这样就等效地完成了采样周期的彼此错开。
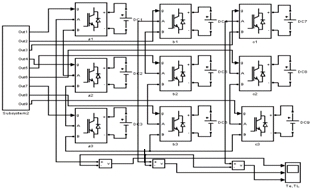
(a) 三级级联多电平逆变器主电路
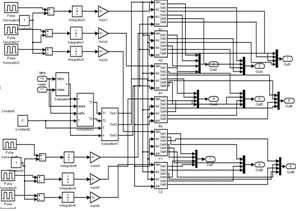
(b)STS-SVM驱动信号发生单元
图4 级联多电平主电路与PWM发生单元
4.2 磁链与转矩观测
定子磁链的估量大体上能够分为三种模型,即u-i模型,i-n模型,u-n模型。其间u-i模型中磁链表达式为
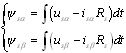 (1)
(1)
其间,,us,is,Rs分别为定子磁链、电压、电流值与定子电阻值,可见,u-i模型观测定子磁链无需转速信息,仅有所需了解的电动机参数是定子电阻Rs,因而非常合适在此处运用。
![]() (2)
(2)
其间,Pn为电机的极对数。
在Matlab/Simulink中树立磁链与转矩观测的模型,如图5所示。
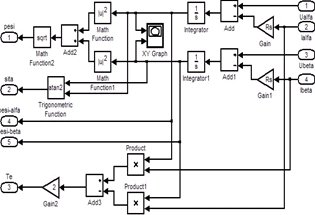
图5 定子磁链与转矩观测模型
4.3 速度估量
根据模型参阅自习惯体系(Model Reference Adaptive System,MRAS)的转速辨识完成较为便利,且具有对转子电阻改变的彻底不敏理性,电机参数改变对转速预算的影响也较小。转子磁链的电压模型与电机转速无关,而转子磁链的电流模型与电机转速有关,因而挑选转子磁链的电压模型作为参阅模型,而挑选转子磁链的电流模型作为可调模型[7]。
因为在磁链观测中现已预算出定子磁链,因而参阅模型能够用定子磁链表明:
![]() (3)
(3)
其间,![]() 为转子磁链,Lm为定转子互感, Lr为转子电感,
为转子磁链,Lm为定转子互感, Lr为转子电感,![]() 为定子瞬时电感, Ls为定子电感。
为定子瞬时电感, Ls为定子电感。
可调模型为:
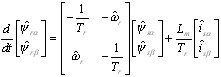 (4)
(4)
其间Tr=Lr/Rr为转子时间常数,Rr为转子电阻,![]() 为转子角速度。
为转子角速度。
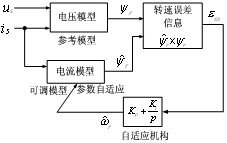
图6 使用转子磁链估量转速的MRAS计划
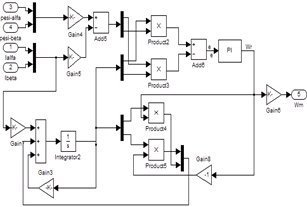
图7 转速估量模型
界说广义状况差错![]() ,使用Popov超安稳准则可推导出自习惯率方式为:
,使用Popov超安稳准则可推导出自习惯率方式为:
![]() (5)
(5)
其间,Kp、Ki分别为份额和积分系数, 是取之于的差错信息,
![]() (6)
(6)
由式(6)能够看出,磁链差错信息份额于转子磁链矢量 和 之间的角差错αr, 经过PI调理器可发生速度信号![]() ,这个调整信号会使可调模型估量的
,这个调整信号会使可调模型估量的![]() 与参阅模型的
与参阅模型的![]() 趋于共同,令转子磁链差错 能够收敛于零,也就会使转速估量值
趋于共同,令转子磁链差错 能够收敛于零,也就会使转速估量值![]() 逐步逼近于实在值
逐步逼近于实在值![]() ,其原理如图6所示。图7为使用转子磁链估量转速的MRAS的Matlab/Si mulink模型。
,其原理如图6所示。图7为使用转子磁链估量转速的MRAS的Matlab/Si mulink模型。
5 仿真成果及剖析
在Matlab/Simulink中树立了整个体系的仿真模型。其间,电机模型选用软件自带的两级三相异步感应电机模型,参数为:额外功率PN =3730W,额外线电压UN =380V,额外频率fN =50Hz,转子电阻Rr=1.083Ω,定子电阻Rs=1.115Ω,定子、转子电感Ls= Lr=0.2097H,定转子互感Lm=0.2037H,转动惯量J=0.02kgg㎡。逆变器每级直流电源电压为104V,采样周期Ts=952µs。
仿真中,给定转速![]() ,电机空载发动,在0.3s处突加6Ngm的负载。各个变量的仿真波形如图8所示。
,电机空载发动,在0.3s处突加6Ngm的负载。各个变量的仿真波形如图8所示。

(a)辨识转速与实践转速

(b)转矩动态相应

(c)定子磁链 (d)电流

(e)相电压

(f)线电压
图8 体系仿真波形
由仿真波形能够看出,电机发动后0.2s,体系根本进入安稳状况;辨识转速能较好地估量与盯梢实践转速;相电压输出7电平;线电压输出13电平;电流波形杰出;稳态时磁链与转矩脉动都比较小;发动过程中定子磁链能很快到达给定值,并坚持圆形;发动时转矩敏捷到达限幅值(23Ngm),之后逐步回落到空载安稳值,加载时动态呼应特性杰出。
6 定论