2.3.2依据混沌振子的弱小信号检测
混沌理论作为一门新学科现已引起了我们的注重,是近年来非线性科学范畴的抢手学科。混沌现在尚无通用、严厉的界说,一般以为,在某些确认性非线性体系中,不需要附加任何随机因素,仅由其内部存在着非线性的彼此作用所发生的类随机现象称为混沌。当体系发生混沌行为时,体系响应对体系参数由噪声发生的摄动并不灵敏,也便是体系的混沌行为对噪声具有必定的免疫力,这类非线性体系行为对参数的依赖性和混沌吸引子对噪声的免疫力使其在弱小特征信号检测方面具有潜在的使用远景。在许多工程实践中,弱小特征信号的发生就标明体系的运转状况发生了改变,怎么检测这些在强噪声搅扰情况下的弱小信号是信号处理中的重要研讨内容。
现在混沌振子用于弱小信号检测的研讨己经越来越深化。混沌振子因为参数的不同会表现出不动点、周期、拟周期、混沌等动力学状况。对两种状况的彼此转化时的参数临界值,在非线性科学中称为“分叉值”,两种状况间的转化称为“分叉”。Duffing振子信号检测技能主要是使用混沌体系的分岔特性来检测外界信号,将待测信号作为Duffing方程周期策动力的摄动,使用初值灵敏性能够获得很高的丈量灵敏度和杰出的抗噪功能。
使用混沌振子检测弱小信号的办法便是将一个非线性含参数体系设定在其参数的临界值邻近,弱小的特征信号作为对分叉参数的摄动,当具有某一弱小的特征信号作为摄动项参加体系时,则非线性体系的定性状况就会发生改变。经过对非线性体系的定性状况有无发生改变进行判别,然后抵达检测弱小特征信号的意图。
由混沌理论知:一类混沌体系在必定条件下对小信号具有灵敏性,一起对噪声具有免疫力,因此使得它在信号检测中十分具有潜力。由非线性理论知:关于一个非线性体系,当其灵敏参数在必定规模存在摄动时,将引起其周期解发生实质改变。由此,能够使用非线性体系的周期解所发生的实质改变来检测弱小信号。
当选用Duffing振子作为非线性体系来检测弱小信号时,让Duffing振子处于混沌和周期解之间的临界状况,将待测信号作为Duffing振子周期策动力的摄动,经过Duffing振子对噪声和方针信号的不同反响来检测方针信号。当待测信号经过Duffing振子时,噪声尽管激烈,辩识体系状况,能够清楚地检测出特定信号是否存在。
使用混沌振子办法能够从很强的噪声信号中检测其间的特征信号是否存在,该办法具有巨大的使用潜力。但这种办法也存在必定的缺点:
1.若体系输出原本便是安稳周期状况,但因为无法事前知道,所以只能经过调查相图,终究证明输出是安稳状况,那么这种判别办法的工作效率是比较低的。
2.依据体系的相轨道图来判别体系的状况,即体系是处于混沌状况仍是现已跃变到了周期状况,也是不行精确的,简略呈现误判。这种判别办法尽管简略、直观,但终归是一种人为的识别办法,所以没有一个严厉含义下的数学判别规范,缺少理论依据。
2.3.3同步堆集法
同步堆集法的原理是使用信号的重复性和噪声的随机性,对信号重复丈量屡次,使信号同相的堆集起来。噪声则无法同相堆集,使信噪比得到改进。在这种办法中,丈量次数越多,则信噪比改进越显着。
若丈量次数为n,则堆集的信号为:
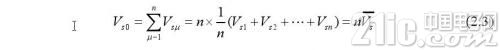
其间,
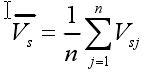
为累积信号的平均值,实践上等于输入信号V si。另一方面,重复丈量n次后,依据各次噪声的不相关性,则堆集的噪声等于:
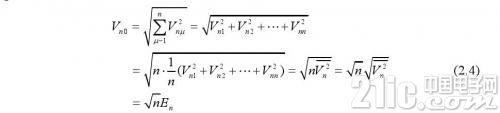
上式中最终的E n为累积噪声的均方根值。

得到信噪比为:因此,丈量次数n越大,则信噪比的改进越显着。而添加丈量次数,就意味着延伸丈量时刻,所以信噪比的改进是以耗时刻换来的。
同步累积器的原理框图如图2.5所示:

其间V 1(t)为输入信号,V 2(t)为与V 1(t)周期相同的参阅信号,同步开关受V 2(t)
发生的操控信号操控,确保V 1(t)在累积器中同相的累积起来。
要确保做到同相累积,则要依据不同的被检测信号波形,确认不同的参阅信号。在实践使用同步累积法的时分,必需满意以下条件:信号应为周期信号,有恰当的累积器,能做到同相累积。
2.3.4双路消噪法
双路消噪法的原理是使用两个通道对输入信号进行不同的处理,然后设法消去一起的噪声,最终得到有用的信号。如图2.6所示。
假定输入信号频率为f 0的正弦波,并混有强的噪声,将其送入上下两个通道。进入上通道的信号经过放大器后,再经过一个中心频率为f 0的窄带带通滤波器,变成正弦波加窄带噪声,这个信号经过正向检波积分后输出一个正极性直流电压,上面叠加了随机崎岖的成分。进入下通道的信号经过放大器后,再经过一个中心频率为f 0的带阻滤波器或陷波器,所以正弦波被滤掉,剩余噪声。噪声经过负向检波积分器后,输出一个在某个负电平上下随机崎岖的电压量。上下两通路各自检波积分后的输出一起送给一个加法器,所以正负极性的噪声电平要抵消一部分,剩余很小的崎岖电压,然后使得输出信噪比得到进步。加法器出来的信号,最终再经过一个阈值电路进行计数。加法器一般能够做成可调,使得无正弦波而仅有噪声时,加法器的输出略为正,可是不超越阈值电路的阈值电平,因此计数器一般无计数。但考虑到加法器输出的电压有崎岖,所以,有时会有高于阈值的脉冲电压经过阈值电路发生本底计数,但因为噪声的计算性,本底计数的次数在某个必定的时刻内t是一个稳定值,能够经过试验测出这个时刻t.假如输入信号中有正弦波存在,那么在这个时刻t内的计数就会添加。所以,经过调查t时刻内计数的改变,就能够判别正弦波信号是否存在。
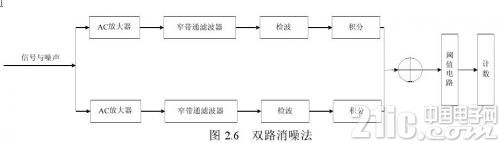
因为信号与噪声性质彻底不同,信号一般为改变规则的量,而噪声是一些随机量,满意计算规则。依据这个条件,能够选用双路消噪法进行信号检测。当随机性的噪声从两路抵达加法器时,噪声极性正好相反,经过加法器相加后把噪声消除。只要少量噪声才经过阀值电路而发生本底计数。依据计算规则,本地计数时刻较长时为稳定值,能够先测出其值,然后从总计数中把它减掉,得到信号计数。
可是这种办法只能检测到弱小的正弦信号是否存在,而不能复现其波。
2.3.5窄带滤波法
窄带滤波法的原理是使用信号的功率谱密度较窄,而噪声的功率谱相对很宽的特色。使用一个窄的带通滤波器,将有用信号的功率提取出来。因为窄带通滤波器只让噪声功率的很小一部分经过,而滤掉了大部分的噪声功率,所以输出信噪比能得到很大的进步。
假若噪声为白噪声,其功率谱密度为常数N 0,K v为窄带滤波器的增益,让白噪声经过一个带宽为B=f 2 -f l的滤波器后,输出噪声电压的均方值为:
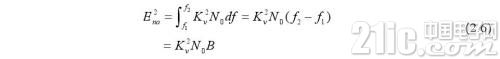
上式可看出:噪声输出总功率与体系的带宽成正比,能够经过减小体系带宽来减小输出的白噪声功率。即通频带越越窄,噪声电压均方值越小,按捺噪声的才能越强,然后抵达信号检测的意图。
假若噪声为1/f噪声,经过与上述相同的体系之后,其输出噪声即由1/f噪声发生的输出噪声功率为:
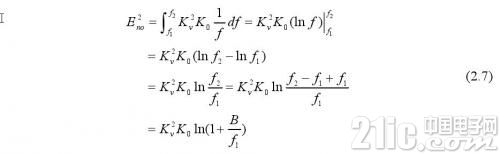
上式可看出:经过减小通频带B来减小输出端的1/f噪声功率。
窄带通滤波器的完成办法许多。常见的有双T选频,LC调谐,晶体窄带滤波器,锁定放大器和取样积分器等。其间双T选频能够做到相对带宽等于千分之几左右,晶体窄带滤波器能够做到万分之几左右。即便这样,这些滤波器的带宽仍是较宽,因为这种办法不能检测深埋在噪声中的信号,一般它只用在对噪声特性要求不是很高的场合。
窄带滤波法能削减噪声对有用信号的影响,滤除通频带以外的噪声,进步信号的信噪比。可是,因为滤波器的中心滤波频率不安稳,不能满意更高的滤除噪声的要求。此外,若信号极端弱小,吞没在噪声之中,那么窄带滤波器的输出信号尽管噪声电压均方值小了,信噪比也进步了,可是弱小信号依然被噪声所吞没。