0 导言
模数转化器(ADC)在信号处理中起了一个非常重要的效果。在数字音频、数字电视、图画编码及频率组成等范畴需求很多的数据转化器。因为超大规划集成电路的尺度和偏压不断减小,模仿器材的精度和动态规划也不断下降,关于完成高分辨率的ADC是一种应战。高阶多位Delta-sigma ADC因为不需求采样坚持电路,电路规划小,能够完成较高的分辨率,因而在实践中得到广泛的运用。Delta-sigmaADC采用过采样技能和噪声整形技能相结合,对量化噪声两层按捺,然后完成高精度模数转化。在实践的规划中需求依据规划目标稳定性和动态规划等进行折衷。要完成大的动态规划,就需求较高的过采样率和多位量化器。为了坚持高阶DSM的稳定性就需求运用多位量化器,而多位量化器会添加后续内部ADC的规划难度。因而,有必要细心挑选过采样率和量化器的位数,以完成预期的性能目标。本文提出一种三阶单环部分反应的Delta-sigma调制器结构,运用Richard Schreier的Matlab Delta-sigma调制器规划工具包,推导调制器传输函数,并对系数进行优化,运用Verilog硬件言语对调制器进行行为级建模。调制器的信号带宽为32.8kHz,过采样率为128,作业时钟8.4MHZ,精度16位,能够到达145dB以上的SNR。
1 Delta-sigma调制器的原理和结构
△-∑调制技能来自高分辨率的A/D、D/A变换器中的过取样△-∑转化技能,运用经典自动控制理论中负反应概念,经过反应环来进步量化器的有用分辨率并整形其量化噪声。在对信号进行过取样后,噪声功率谱起伏下降,并经过一个对输入呈低通而对量化噪声出现高通的噪声整形器,将量化噪声功率的绝大部分移到信号频带之外,然后可经过滤波有用地按捺噪声。
Delta-sigma调制器的仿真模型能够用图1来表明。该体系是一个双端输入、单端输出的线性体系,体系的一个输入为外部输入信号U,另一个输入为量化器的反应V,输出则是量化器的输入Y。
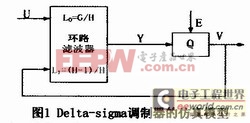
由图1依据叠加原理,可知体系的输出能够表明为
其间,L0(z)和L1(z)分别是输入U(z)和V(z)到输出Y(z)的传递函数。
令调制器量化噪声为E(z),则调制器的输出为
由式(1)、(2)可得

其间G(z)是信号传递函数(STF),H(z)是NTF(NTF)。所以