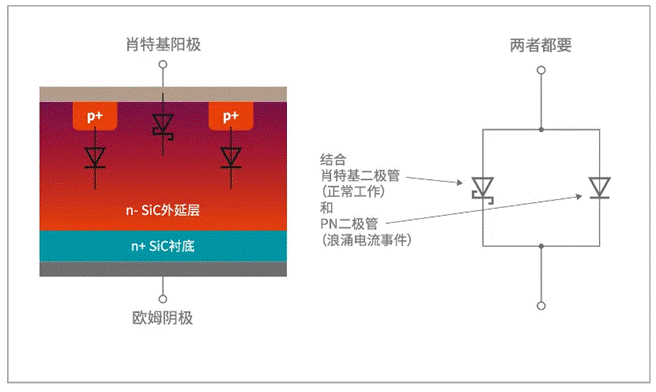
电感位移传感器被广泛使用于细小位移量检测中,但在一些工程中现有传感器的丈量精度和灵敏度达不到丈量要求。针对这一问题,对传感器前段信号处理电路进行改进,在传感器上下线圈并联电容构成LC电路,运用LC电路谐振效应改进电路的功能,以进步信号源头的灵敏度;选用Multisim软件对半桥和全桥电路在并联不同巨细的电容后的功能进行仿真,并用Matlab对生成的曲线进行最小二乘拟合,比较得出使电路功能最优的电容值和并联办法。成果表明在丢失细小线性度的状况下可将灵敏度进步一倍。
电感位移传感器的本质,是将灵敏元件的改动量转化成电压幅值的改动量来进行丈量,其广泛使用于检测细小位移量的检测体系中,因而对电感传感器的丈量精度和灵敏度要求很高。电感位移传感器的灵敏度是指输出电压的增量与侧头位移增量的比。在其他条件相同的状况下进步灵敏度能够进步体系的最小分辨率和精度。进步电感传感器灵敏度的办法有多种,但现在首要都是经过对电感传感器的信号调度电路的改进来完成。文中测验经过谐振电路改动传感器的输出信号,从信号源头增大传感器灵敏度。这种办法相当于对传感器本身进行改进,使得它还能够与其他改进技能如:传感器鼓励源、输出信号处理、核算机软件补偿等兼容以共同进步整个体系的功能。
1 改进后电路的模型树立
1.1 半桥式改进电路
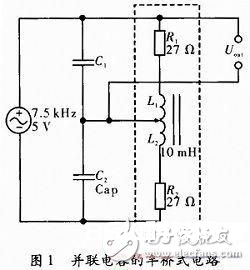
如图1假如没有C1和C2为一般半桥电路,虚线框中为电感传感器的等效电路,传感器测头的位移带动螺线管中铁芯上下移动,然后改动上下两个线圈的电感值。将两线圈等效成纯电阻和纯电感的串联,如图中R1和L1组成上线圈,R2和L2组成下线圈,输出接在上线圈上。实践传感器中线圈与输出的接线不会变,仅仅经过铁芯移动来改动电感,所以R1和R2固定不变。输出电压
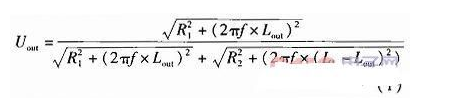
图1在上下两个线圈并联电容C1和C2后,别离构成了谐振回路I和回路II。假如铁芯在最下方时:回路II谐振,回路I失谐。当铁芯在最上方时:回路I谐振,回路II失谐。由于谐振电路在谐振时的阻抗会远大于失谐时的阻抗。能够定性地得出,铁芯在最下方时Uout的幅值会比没有电容小,在最上方时会比没有电容时大,所以灵敏度会增大。但在最下方和最上方中心的改动状况,以及它的线性度则需求后边仿真来确认。输出电压

1.2 全桥式改进电路
一般全桥电路图2(a),传感器上下两线圈别离与匹配电阻R3和R4相连,在L1=L2时电桥平衡,当向上产生△X的位移时,铁芯上移,L1增大△L,L2减小△L,Uout的改动会比半桥办法添加近两倍,输出电压
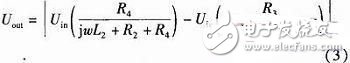
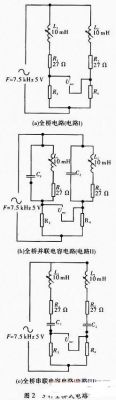
如图2(b)和图2(c)对上下两线圈别离选用并联和串联电容C1和C2的办法,构成谐振回路I和回路II,经过后续仿真调查这两种办法电路功能的改动状况。输出电压

2 电路的仿真
2.1 仿真渠道及仿真条件
仿真渠道运用MulTIsim,它是美国国家仪器(NI)有限公司推出的以Windows为根底的仿真东西,适用于板级的模仿/数字电路板的规划作业。它包含了电路原理图的图形输入、电路硬件描绘言语输入办法,具有巨大的元器件库和全面的仪器仪表库和丰厚的仿真剖析才能。选用它来对改进前后的电路进行仿真。
在仿真之前,先结合工程实践状况对仿真条件进行一些设定:
(1)鼓励电源:频率为7.5 kHz,峰峰值为5 V的交流电。
(2)传感器:总电感值为10mH差动电感传感器,线性规模为3~7mH,电感的本身的电阻值为54Ω。
如上文所述R1和R2固定不变,所以R1和R2为27Ω。而对应的纯电感L1和L2,会跟着位移线行改动,满意L1+L2=10 mH(3《L1《7,3《L2《7)。
2.2 仿真进程及成果
关于半桥时电路II由于期望铁芯在最下方时回路II谐振,最上方时回路I谐振,由于L1和L2的改动规模为3~7 mH。L2为7 mH时回路II谐振,L1为7 mH时回路I谐振。依照仿真条件核算C1=C2=65 nF。简化仿真无妨取C1=C2,在65 nF邻近从55~100 nF距离5 nF进行仿真,调查电路功能,仿真成果如图3所示。
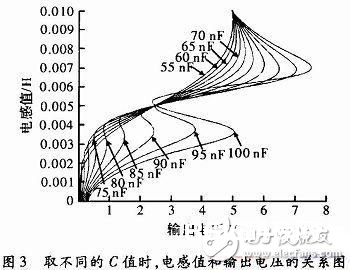
图中能够看出不同的电容值对电路的功能影响很大,假如挑选不恰当,反而会使体系功能下降。只要挑选恰当容量的电容巨细才能使丈量灵敏度进步,一起坚持尽量小的线性差错。所以选取曲线在L1=3~7 mH段时,灵敏度最高,线性度最好,进行最小二乘核算,它与一般半桥的比照如图4所示。
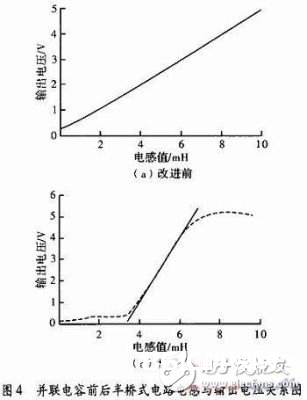
经Matlab核算一般半桥在3~7 mH段,电压改动规模1.5~3.5 V,电压对电感的灵敏度为0.5V/mH。线性度近似为1。对图4(b)选用最小二乘法拟合直线后,在3.8~6.3 mH段,输出电压的改动规模0.77~4.39 V。线性度可达2.39%,灵敏度为1.448 V/mH。
对全桥电路的仿真与半桥的办法相似,需求留意的是期望电桥在L1=L2=5 mL时平衡,所以关于匹配电阻的选取需求依据仿真条件核算
关于电路I:R3=R4=|jw×0.005+R1|=237 Ω;电路II:R3=R4=|(jwL+R1)∥(1/jwC1)|=817Ω;电路III:R3=R4=|jwL+R1+(1/jwC1)|=98Ω。
关于运用电容的电路,相同对不同的电容值条件下的电路进行仿真,选出功能最好的如图5所示。
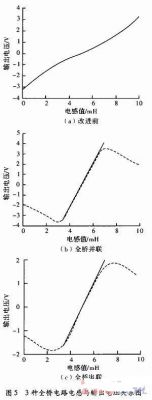
一般全桥在3.8~6.3 mH段,电压改动规模为-1.2~+1.3 V,电压对电感的灵敏度为1 V/mH。线性度近似为1.38。对图5(b)和图5(c)运用Matlab进行最小拟合直线如图所示,在3.8~6.3 mH段,并联办法输出电压的改动规模为-2.66~+2.66V,灵敏度为2.130V/mH线性度可达1.68%。串联办法的输出电压规模约为-1.25~+1.25V,灵敏度约为2.130V/mH线性度可达1.33%。
3 剖析与定论
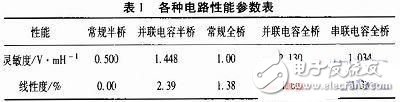
如表1所示,为各电路的灵敏度和线性度,能够在丢失较小线性度条件下,将灵敏度进步。关于半桥尽管将灵敏度进步了近200%,但献身的线性度较大。串联电容的办法灵敏度几乎没有增大。功能最好的是并联电容后的全桥电路,灵敏度提升了113%,且丢失的线性度较小,只比本来增大21.7%,并且实践使用中,能够经过软件补偿和事前标定来弥补线性度的缺乏。
归纳理论剖析和仿真成果,在鼓励源确认和电感传感器参数确认的状况下,经过核算能够得到一个恰当的电容值,当在传感器的两部分线圈上并联这个电容时,丈量的灵敏度会有明显进步,一起仍能够坚持较好的线性度,然后到达改进和进步电感传感器功能和最小分辨率的意图。