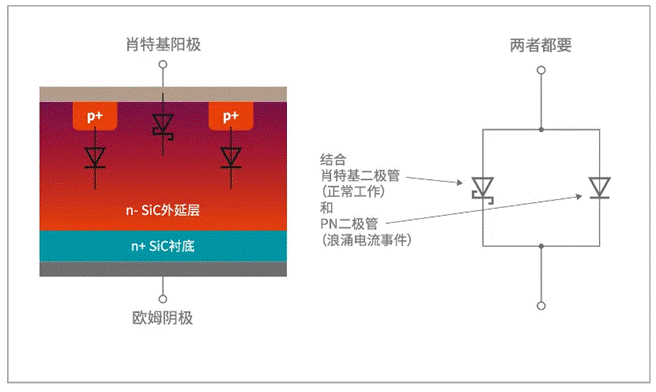
1 概述
Σ-Δ调制是现在国际上的A/D转化器规划中很受欢迎的一种技能,与传统的Nyquist频率采样的A/D转化器作业原理有所不同,选用的是过采样和低位量化结合的办法。其间,过采样技能在模/数混合电路中的运用,能够防止传统A/D或D/A转化办法完成中遇到的诸多困难,尤其是在对低频信号要求高分辨率的运用领域,传统转化办法需求较高精度的模仿结构(模仿电阻、电容等),然后使整个A/D转化器的本钱很高。Σ-ΔADC能够防止运用高精度模仿电路,将噪声面向高频,具有分辨率高,量化结构简略等长处。因为电磁环境日益恶化,对接收机的动态规模要求越来越高,跳频、扩频等宽带信号的运用又要求运用宽带丈量设备,这些都对ADC的分辨率和速度提出了更高的要求。
调制器(Modulator)归于Σ-ΔADC电路中的模仿电路部分,它的结构挑选和电路参数规划都极大地影响着整个ADC的信噪比(SNR)等功能指标。在Σ-Δ调制器中,运用了过采样、噪声成形等关键技能。这些技能还使它别的具有一系列固有的长处,如易于与数字信号处理体系单片集成,无须采样坚持电路,对输入端抗混迭滤波器要求很低一级。下面先评论过采样与MASH噪声成形的首要单元剖析,最终针对DAC失真差错,规划并仿真了一种数字差错校对技能。
2 根本原理与技能
2.1 Σ-ΔADC根本原理及调制器的组成
Σ-ΔADC由两部分组成:调制器和数字抽取滤波器。其间调制器的作业原理是选用远远大于Nyquist频率的时钟对输入模仿信号进行”过采样”,采样频率与Nyquist频率之比界说为过采样率M,是调制器的重要结构参数之一。因为采样频率很高,则无需传统的PCMADC中的坚持电路。采样后的信号与前一时刻的采样信号比较较,对其差值做出低位量化,输出低位码流,并依据量化器的输出决议回来+Δ或-Δ反应信号。调制器的根本结构如图1所示,首要由采样环节、积分器、量化器以及D/A反应组成,其间fs表明采样时钟频率,K1,K2别离表明输入信号和反应信号的增益系数。
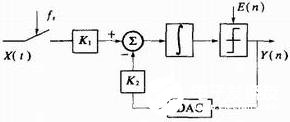
图1 Σ-Δ调制器根本结构
习惯上,界说调制器中含有的积分器个数为调制器的阶数L,量化器的个数为级数。对调制器的线性模型做离散域的z变换剖析,并将量化差错模型化为噪声信号,能够推导出输出信号Y对输入信号X与量化差错E的传递函数,在有用信号频率内,输入信号坚持不变而噪声信号被差分衰减,即
Y(z)=z-LX(z)+(1-z-1)LE(z) (1)
一般,对调制器功能评测的重要参数之一是信噪比SNR,即信号功率与噪声功率之比
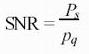 (2)
(2)
这儿ps为有用信号的功率,对正弦信号来说,ps=
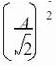
,A为起伏;pq是信号频带内总的量化噪声功率,由E(z)的传递函数在有用信号频带内积分得到
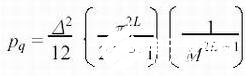
(3)
从上式能够看出,别离进步M或L都能带来SNR的进步。但当信号频率到达几十MHz以上的高频规模后,M的进步势必会遭到现有工艺,以及功耗等限制。现在,更多的研讨改进SNR的办法是针对L的进步。
从调制器内涵安稳性考虑,针对高阶调制器(L≥3),又有两种结构上的取向,即单级single-loop结构和多级级联的MASH结构。
2.2 过采样及MASH(多级噪声成形)技能
本文中运用记号fN来表明Nyquist调制器作业时的采样率,而它与基带信号最高频率fB的联系工程上一般为fN≈2.2fB~2.5fB。所谓过采样,就是指采样速度fs远大于fN。这儿称M=fs/fN为“过采样比”。在Σ-ΔADC的规划中,M远大于1,且取为2的整数次幂(如32、64等)。过采样带来的长处为紧缩基带内量化噪声,下降对输入端模仿滤波器的要求等。
可是,光凭过采样来紧缩基带内噪声是低效率的,进步4倍采样率才相当于进步1bit分辨率。为了更有用地衰减基带内量化噪声,应在过采样条件下进一步参加噪声成形(noise shaping)技能。最根本的一阶噪声成形器即所谓的一阶Σ-Δ调制器,其原理此处不再评论。这儿只指出,它可被转化为如图2所示的离散时刻等效模型。
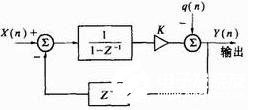
图2 一阶Σ-Δ调制器离散时刻等效模型
图2中的积分器用I(z)=(1-z-1)-1等效描绘,而1bit ADC被加性噪声源q(n)代替。嵌在反应环路中的1bit DAC被一个单位时延z-1替代,以防止在离散时刻模型中呈现无时延反应环。q(n)是与输入信号无关的白噪声,用它能够方便地描绘Σ-Δ调制器在很多信号作用下的均匀行为,剖析可得其输入、输出联系式为
Y(z)=X(z)+(1-z-1)Q(z) (4)
由上式可知,在信号频谱X(z)未变的一起,白噪声Q(z)被(1-z-1)加权而成为“高通”形状。此现象正是所谓“噪声成形”。加权函数(1-e-j2πfT)的零点f=0使得基带内噪声被大大紧缩;而在带外的高频端,噪声却略有上升。
在实践运用中,为更有用地压低量化噪声到达分辨率要求,还得考虑高阶噪声成形。一般地,将L个一阶Σ-Δ调制器组合起来,能够完成(1-z-1)L(L阶噪声成形)。
规范的MASH(Multistage Noise Shaping,多级噪声成形)结构如图3。它实践上是L个一阶Σ-Δ调制器的串联,其间前一级调制器内的1bit ADC的量化差错被送入下一级进行再量化,然后将各级的输出码流送入运算节点进行处理。最终输出了经(1-z-1)L成形处理后的低分辨率码流。明显,这样的前馈结构不会存在任何安稳方面的问题。
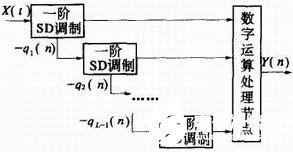
图3 MASH结构框图
MASH中的数字处理节点所做的作业是抵消各级的量化差错:
榜首级:Y1(z)=X(z)+(1-z-1)Q1(z),将-Q1(z)送入第2级,有Y2(z)=-Q1(z)+(1-z-1)Q2(z),再将-Q2(z)送入第3级,有Y3(z)=-Q2(z)+(1-z-1)Q3(z),。.直至YL(z)=-QL-1(z)+(1-z-1)QL(z),而运算节点使得
Y(z)=Y1(z)+(1-z-1)Y2(z)+.。.+(1-z-1)L-1YL(z)=X(z)+(1-z-1)LQL(z) (5)
这样,就等效完成了(1-z-1)L噪声成形。除MASH外,还有许多新颖的选用计算机辅助规划的Σ-Δ噪声成形计划,用其可完成更高效的噪声成形。
3 一种DAC非线性差错校对办法
在MASHΣ-ΔADC中,与一位(1bit)量化比较,选用多位量化用具有增大信噪比(SNR),添加安稳性以及下降运算放大器标准等长处。可是,内部DAC的非线性导致功能瓶颈,一般要求其最少具有与整个ADC相同好的线性。现在,关于较大过采样比(OSR>32),选用即时数字校准、失配整形可解决此问题。但在宽带ADC中,OSR较小(一般≤4),失配整形法就变得无效。本文描绘了一种数字即时校准办法。不同于较早的技能,其对低过采样比状况有用。而且,此办法能够跟从漂移。
3.1 校对体系
以二阶Σ-Δ调制器(DS1)为例来阐明给出的校对技能。如图4所示,内部DAC有两个输出:v1和vT,别离输入到循环滤波和校准ADC(DS2)。由校准ADC得到^eD,即一切输出电平的DAC差错eD的数字估量,而且其被存储在RAM中。在转化时,经过FIR滤波器NLF(z)过滤RAM的输出,然后校对内部DAC差错,并从DS1的数字输出d1中减去过滤输出成果。取得^eD的进程和体系的详细剖析在以下内容中给出。
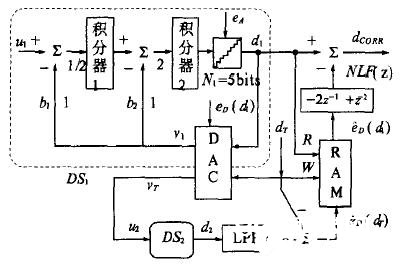
图4 带有差错校对的Σ-Δ调制器
在图4所示体系中,假定独自DAC输出为两个积分器供给反应信号。系数b1、b2的不匹配对体系线性没有影响。值得注意的是,体系没有对内部ADC的非线性差错进行校对。这些差错被与量化噪声相同的噪声传输函数所按捺,其很少作为问题提出。当运用很低的OSR时,这样是不行的,就高线性而言,需求添加阶数或运用ADC元件失配整形。
3.2 校对办法
实践DAC输出电平差错的即时取得适应于DAC的结构。假如DAC可供给多重输入和输出,那么离线校准能够被传输到后台进程。假如那样,关于DAC的每个或许的输入,数字校准信号dT将供给阶梯波形。经过校准Σ-Δ转化器DS2,每个DAC输出电平vT被转化成数字方式d2,然后经过LPF低通滤波而消除DS2的量化差错。然后,减去dT然后补偿电平差错eD,这样,得到差错估量^eD并将其存储在RAM中,而且对每一输出d1将再次调用^eD并校对。在运转进程中,周期性地重复校准,以追寻DAC输出电平中发生的漂移。
在低过采样率(OSR)和低阶循环滤波器情况下,从DAC的输出v1到DS1的输出d1的传输函数不能由NLF(z)=-1正确地近似。为了得到准确的差错校准,如图4所示,RAM的输出需求被实践的NLF(z)(此处为-2z-1+z-2)过滤。
在一些DAC的完成中,运用了N个等价单位元件(电流源、电容、电阻等)。假如在DAC中履行N+1个元件,可运用上述算法,运用DS2逐一次序地丈量它们的差错。换句话说,输出信号d1与校准信号dT相同可被运用。运用n个单位元件经过调用d1值然后发生v1,剩下的N-n个单位元件被用来发生vT。假如DAC增益和偏移差错是能够被承受的,为了使一切单位元件差错总和可取零,那么vT中的差错是v1中差错的负数。因而,经过将vT中的模仿采样分类进入通道,运用其间一个通道专用于每个或许输入(d1)码和其补码,DS2可用来以数字方式发生独自DAC电平。因为为每一DAC电平仿制存储元件(反应电容),DS2的运算可容易地在通道中多重复用。
因为线性运算,校准ADC(DS2)本身有必要要有高的线性。这需求在DS2中运用1位内部量化器。可是,因为DAC非线性信息坚持,线性影响(增益和偏移差错)在DS2中是能够承受的。相同,实践DAC差错传输函数(从v1至d1)和其数字仿制部分NLF(z)之间的匹配差错对整个转化器的线性仅有较小的影响。
3.3 仿真成果
数字校对ADC(如图4的DS2)的运转仿真条件如下述。假定5bit(322电平)内部ADC和DAC,在DAC中有0.1%线性梯度差错。这契合中等差错0.4%的要求。在一切电路中,一切运放和恣意失配电容(有0.1%规范偏差)的有限直流增益设定为54dB。运用OSR=4。在DS1中参加峰值为0.45V的中频双腔调输入信号u1,选用二阶单位Σ-ΔADC完成DS2。为了证明运用校准可得到的高线性,DS1被接入在220MASH(包括10bitADC作为其第二级)中。这儿不考虑在MASH(多级噪声整形)各级中的失配,它相同可由数字办法校对。
选用抱负DAC、非抱负运放和电容,体系运转计算出的频谱如图5(a)所示。图5(b)给出了运用差错校准的非线性DAC得到的频谱。能够看出,发生了大的谐波,SFDR仅为52dB。当运用了本文提出的数字校对技能后,频谱成果如图5(c)所示,得到SFDR>100dB。为了得到这样高的SFDR所需求的充沛准确的eD估量,DS2对DAC的每一电平进行了218采样(假如DS2时钟控制在fs=5MHz,那么后台校准完好循环需求约4秒)。最终,图5(d)阐明晰运用NLF(z)=-1后的有害影响,即SFDR由101dB降至60dB。
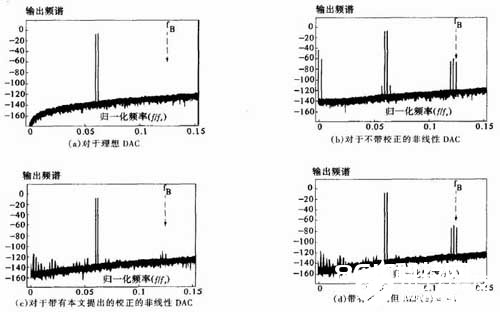
图5 MASH的输出频谱(215采样,64倍FFT,fB=fs/8,OSR=4)
5 定论
本文介绍了Σ-Δ调制器的根本原理和技能,并针对选用多位内部量化器的MASH Σ-ΔADC提出了一种即时数字校对办法。关于低过采样比的模数转化器,选用一般的失配整形技能作用欠安,但本办法可有用运用于此。经过仿真证明,运用本文提出的即时数字校对法可得到极好的线性。
责任编辑:gt