学习相同东西,个人主张须从三个维度进行:What Why How
这儿的内容首要参阅胡广书编写的《《数字信号处理导论》》7.5.1节,加了一些自己的了解。
说到均匀滤波器,做过单片机使用开发的朋友,立刻能想到将一些采样数据进行加和求均匀。诚然如此,从其时域数学描绘而言也很直观:
其间 代表当时丈量值,关于单片机使用而言,可所以当时ADC的采样值或许当时传感器经过一系列处理的物理量(比如在工业操控领域中的温度、压力、流量等丈量值),而 表明上一次的丈量值,以此类推, 则是前第N-1次丈量值。
为了提醒其更深层次的机理,这儿用Z传递函数将上述公式进一步描绘:
关于傅立叶改换而言:
Z改换的实质是拉普拉斯改换的离散化方式, ,令 ,则
令 ,则
)
所以,均匀滤波器的频率呼应为:
幅频相频呼应剖析
使用下面的python代码,来剖析一下
# encoding: UTF-8
fromscipy.optimize importnewton
fromscipy.signal importfreqz, dimpulse, dstep
frommath importsin, cos, sqrt, pi
importnumpy asnp
importmatplotlib.pyplot asplt
importsys
reload(sys)
sys.setdefaultencoding( ‘utf8’)
#函数用于核算移动均匀滤波器的截止频率
defget_filter_cutoff(N, **kwargs):
func = lambdaw: sin(N*w/ 2) – N/sqrt( 2) * sin(w/ 2)
deriv = lambdaw: cos(N*w/ 2) * N/ 2- N/sqrt( 2) * cos(w/ 2) / 2
omega_0 = pi/N # StarTIng condiTIon: halfway the first period of sin
returnnewton(func, omega_0, deriv, **kwargs)
#设置采样率
sample_rate = 200#Hz
N = 7
# 核算截止频率
w_c = get_filter_cutoff(N)
cutoff_freq = w_c * sample_rate / ( 2* pi)
# 滤波器参数
b = np.ones(N)
a = np.array([N] + [ 0]*(N -1))
#频率呼应
w, h = freqz(b, a, worN= 4096)
#转为频率
w *= sample_rate / ( 2* pi)
#制作波特图
plt.subplot( 2, 1, 1)
plt.supTItle( “Bode”)
#转换为分贝
plt.plot(w, 20* np.log10(abs(h)))
plt.ylabel( ‘Magnitude [dB]’)
plt.xlim( 0, sample_rate / 2)
plt.ylim( -60, 10)
plt.axvline(cutoff_freq, color= ‘red’)
plt.axhline( -3.01, linewidth= 0.8, color= ‘black’, linestyle= ‘:’)
# 相频呼应
plt.subplot( 2, 1, 2)
plt.plot(w, 180* np.angle(h) / pi)
plt.xlabel( ‘Frequency [Hz]’)
plt.ylabel( ‘Phase [°]’)
plt.xlim( 0, sample_rate / 2)
plt.ylim( -180, 90)
plt.yTIcks([ -180, -135, -90, -45, 0, 45, 90])
plt.axvline(cutoff_freq, color= ‘red’)
plt.show
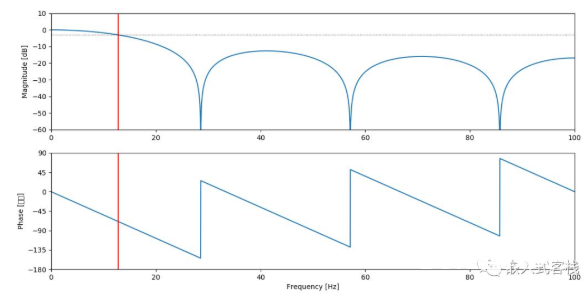
取采样率为200Hz,滤波器长度为7可得下面的幅频、相频呼应曲线。从其主瓣可见其幅频呼应为一低通滤波器。幅频呼应略有不平,随频率上升而衰减。其相频呼应线性。假如对滤波器有经历的朋友会知道FIR滤波器的相频呼应是线性的,而移动均匀滤波器刚好是FIR的一种特例。
当改动滤波器长度为3/7/21时,仅调查其幅频呼应:
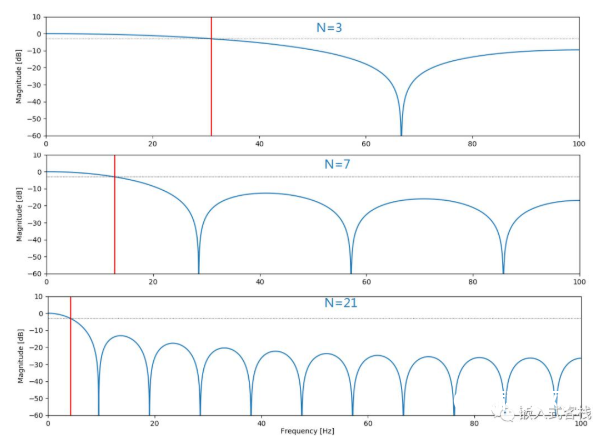
可见,跟着滤波器的长度变长,其截止频率变小,其通带变窄。滤波器的呼应变慢,推迟变大。所以实际使用的时分,须根据有用频率带宽合理挑选滤波器的长度。有用信号的带宽能够经过按采样率收集必定的点进行傅立叶剖析可得。假如有带FFT功用的示波器,也能够直接丈量得到。
C言语完成
滤波器的C言语完成,比较简单。干货在此,快快领走
# defineMVF_LENGTH 5
typedeffloatE_SAMPLE;
/*界说移动均匀寄存器前史状况*/
typedefstruct_ t_MAF
{
E_SAMPLE buffer[MVF_LENGTH];
E_SAMPLE sum;
intindex;
}t_MAF;
voidmoving_average_filter_init(t_MAF * pMaf)
{
pMaf-》index = -1;
pMaf-》sum = 0;
}
E_SAMPLE moving_average_filter(t_MAF * pMaf,E_SAMPLE xn)
{
E_SAMPLE yn= 0;
inti= 0;
if(pMaf-》index == -1)
{
for(i = 0; i 《 MVF_LENGTH; i++)
{
pMaf-》buffer = xn;
}
pMaf-》sum = xn*MVF_LENGTH;
pMaf-》index = 0;
}
else
{
pMaf-》sum -= pMaf-》buffer[pMaf-》index];
pMaf-》buffer[pMaf-》index] = xn;
pMaf-》sum += xn;
pMaf-》index++;
if(pMaf-》index》=MVF_LENGTH)
pMaf-》index = 0;
}
yn = pMaf-》sum/MVF_LENGTH;
returnyn;
}
测验代码:
# defineSAMPLE_RATE 500.0f
# defineSAMPLE_SIZE 256
# definePI 3.415926f
intmain
{
E_SAMPLE rawSin[SAMPLE_SIZE];
E_SAMPLE outSin[SAMPLE_SIZE];
E_SAMPLE rawSquare[SAMPLE_SIZE];
E_SAMPLE outSquare[SAMPLE_SIZE];
t_MAF mvf;
FILE *pFile=fopen( “。/simulationSin.csv”, “wt+”);
/*方波测验*/
if(pFile== NULL)
{
printf( “simulationSin.csv opened failed”);
return-1;
}
for( inti= 0;i《SAMPLE_SIZE;i++)
{
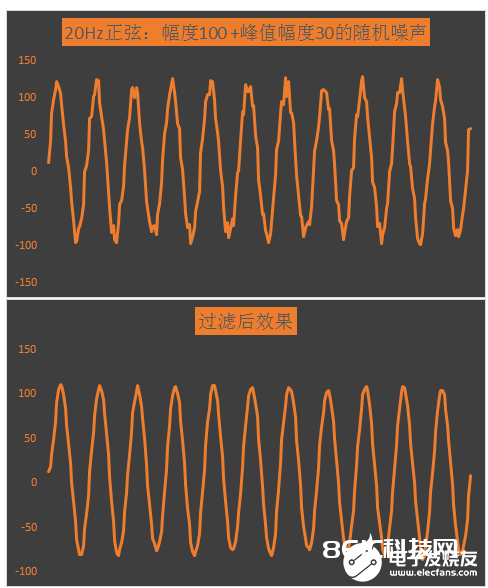
rawSin = 100* sin( 2*PI* 20*i/SAMPLE_RATE)+rand% 30;
}
/*正弦信号测验*/
for( inti= 0;i《SAMPLE_SIZE/ 4;i++)
{
rawSquare = 5+rand% 10;
}
for( inti=SAMPLE_SIZE/ 4;i《 3*SAMPLE_SIZE/ 4;i++)
{
rawSquare = 100+rand% 10;
}
for( inti= 3*SAMPLE_SIZE/ 4;i《SAMPLE_SIZE;i++)
{
rawSquare = 5+rand% 10;
}
/*初始化*/
moving_average_filter_init(&mvf);
/*滤波*/
for( inti= 0;i《SAMPLE_SIZE;i++)
{
outSin=moving_average_filter(&mvf,rawSin);
}
for( inti= 0;i《SAMPLE_SIZE;i++)
{
fprintf(pFile, “%f,”,rawSin);
}
fprintf(pFile, “n”);
for( inti= 0;i《SAMPLE_SIZE;i++)
{
fprintf(pFile, “%f,”,outSin);
}
fclose(pFile);
pFile=fopen( “。/simulationSquare.csv”, “wt+”);
if(pFile== NULL)
{
printf( “simulationSquare.csv opened failed”);
return-1;
}
/*初始化*/
moving_average_filter_init(&mvf);
/*滤波*/
for( inti= 0;i《SAMPLE_SIZE;i++)
{
outSquare=moving_average_filter(&mvf,rawSquare);
}
for( inti= 0;i《SAMPLE_SIZE;i++)
{
fprintf(pFile, “%f,”,rawSquare);
}
fprintf(pFile, “n”);
for( inti= 0;i《SAMPLE_SIZE;i++)
{
fprintf(pFile, “%f,”,outSquare);
}
fclose(pFile);
return0;
}
关于方波测验,使用excel生成波形,可得如下的波形。从波形显着可见,长度为7的移动均匀滤波器关于随机噪声的滤波作用比较满意。从图中还能够看出,移动均匀滤波器在信号链中会引进必定的延时,在使用时需求考虑。关于一般的传感丈量假如没有清晰的要求,常常能够疏忽。
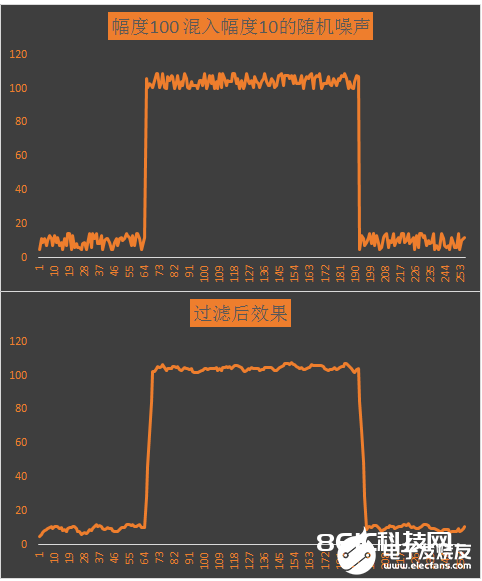
关于正弦信号而言,移动均匀滤波器也有比较显着的作用,仅仅其通带比较窄,假如有用信号频率比较高,则移动均匀滤波器将不合适。