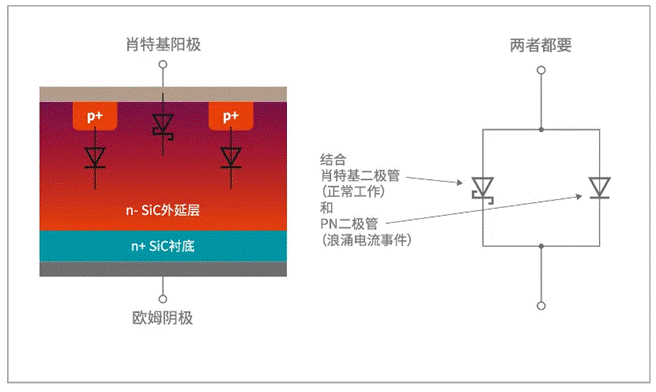
近年来，PMMA 塑料以其优秀的特性被汽车工业垂青，是较为抱负并有发展前景的轻质资料。PMMA 俗称亚克力或有机玻璃，密度为1.19g/cm3，约为无机玻璃的1/2，具有杰出的光学功能和耐候功能，是一种可回收的热塑性工程资料。PMMA 现在首要应用于尾灯车灯、表里饰、三角窗，应用于车门侧窗还比较少。比较固定的三角窗， 车门侧窗作为移动窗，对玻璃的升降运动功能提出了更高的要求，而玻璃升降运动误差是侧窗玻璃重视的首要功能之一。运动误差较大或许会导致升降缓慢乃至发生显着的噪声异响，一起或许还会影响车门的防雨防风及隔声功能。其间，玻璃型面的规划和升降导轨确实定是影响运动误差的两个关键因素。
国表里有许多研讨人员对双曲面玻璃及其升降导轨进行了较为深化的研讨， 其间包含：同济大学的高云凯教授、同济同捷科技股份有限公司的雷雨成教授等选用圆环面办法拟合双曲面玻璃；而且使用UG 等软件完成了圆环面玻璃的几许规划和运动误差剖析。福特公司的Singh 等人凭借CAE 剖析办法研讨了车门玻璃在升降运动过程中的误差以及密封条变形。可是研讨人员首要在双曲面车门玻璃升降导轨规划和仿真误差方面获得必定成果，可是少有人经过实验办法丈量玻璃升降运动的误差，而实验验证始终是查验理论规划的有用办法。实验不只能够考虑车门的出产、制作误差，导槽密封条的效果，这些是仿真中没有考虑的，还能够查验仿真中导轨规划的有用性。
因而，本文提出了一种丈量核算双曲面玻璃运动误差的实验方。一起还提出了一种拟合圆环面的办法，这种办法比文献中的尝试法愈加准确。用仿真和实验的办法研讨了PMMA 侧窗的升降运动误差功能。成果表明，PMMA 玻璃仿真与实验的趋势共同，因而验证了仿真中导轨规划的有用的；而PMMA 的运动误差小于无机玻璃，阐明PMMA 的升降运动误差功能优于无机玻璃。
1 玻璃升降运动误差仿真剖析
1.1 拟合升降导轨
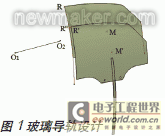
以上海某规划公司的一款A 级车左后门为研讨目标， 针对其双曲面车门玻璃的几许模型， 选用份额函数法拟合其升降导轨导线及导槽导线。依据玻璃圆环面的运动理论可知：抱负情况下，即玻璃曲面不存在运动误差时，玻璃曲面在下降过程中，R 点必定经过R’’点。所以， 车门玻璃下降的过程中，初始方位上的R 点绕轴线O1O2 旋转到R’点，然后再沿轴线O1O2 方向偏移到R’’点，如图1 所示。那么玻璃质心M 点沿相同的圆环面运动时，点M 的运动轨道即为玻璃导轨的导线，规划成果如图2 所示。
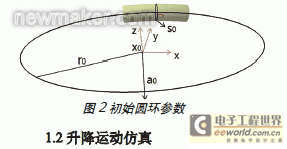
调用DMU Kinematic 模块进行玻璃升降运动仿真，别离丈量玻璃在上止点方位、中心方位及下止点方位时玻璃坐标。
1.3 圆环法拟合玻璃形面
论文在UG 中选取玻璃上的点，经过尝试法拟合的圆环较为粗糙，不能精准确认玻璃型面的方位，因而本文提出一种用圆环法拟合玻璃型面的办法，在matlab 软件中，运用坐标改换和最小二乘的办法较为准确地拟合了圆环面，依据测得的窗框上点的坐标，运用Matlab 软件依据最小二乘法拟合圆环面， 将此圆环面作为玻璃型面，核算玻璃升降运动后间隔圆环面的误差作为玻璃升降运动误差。
（1）选取拟合圆环初始值：
仿真时需求输入的参数为窗框上点的坐标和圆环面的初始参数。其间，圆环初始参数包含：大圆环圆心（X0，Y0， Z0），大圆环的轴线向量
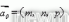，大圆环的半径r0，小圆环的半径s0。如图2 所示，在Catia 中输入窗框的坐标，经过窗框上边际间隔较远的三点确认大圆环， 量取大圆环的圆心、轴线和半径，然后在窗框接近B 柱的边际间隔较远的三点确认小圆环，量取小圆环的半径。 二窗框点的坐标集记为X，其间i 点的坐标为
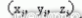。 （2）旋转坐标
由大圆环轴线得到旋转角θ1和θ2，sinθ1、cosθ1、sinθ2和cosθ2可表示为公式（1-4）。经过旋转平移将窗框上的点旋转到以大圆环圆心为原点，Z 轴与圆环轴线相重合的坐标系中。设旋转后窗框上点坐标集为X2，i 点的坐标变为
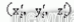，则旋转后的坐标如公式（3） 所示。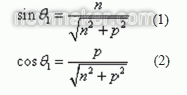 
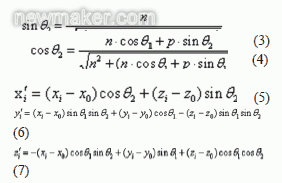
依据公式（8）核算旋转后窗框上点i 到圆环面的间隔 ，用最小二乘法求得误差最小条件下的圆环参数，如公式（9） 所示。
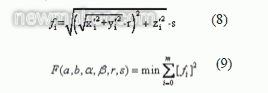
最终，经过旋转平移得到在原坐标系下的圆环面参数：x0n=（15633，560，- 22182），an=（8359，55，5489）， rn=26395，sn=1168.2。
1.4 核算运动误差
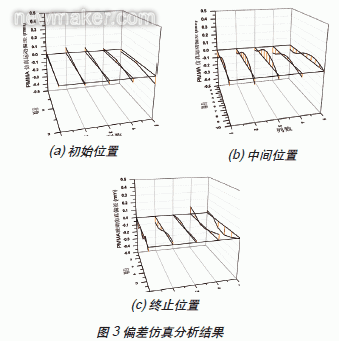
当玻璃运动到不同方位时， 核算玻璃上样本点间隔圆环面的间隔， 得到玻璃的升降运动误差， 其剖析成果如图3 所示。
2.1 实验环境与设备
实验首要选用HXY 系列单臂三维丈量划线仪，也便是三坐标丈量仪。实验环境温度： 30℃ -32℃。玻璃运动误差实验验证设备如图6 所示。
