导言
跟着电压等级的不断进步与电力体系规划的逐步扩展,传统高压测验设备的绝缘问题日益突出,各种旨在处理超高压绝缘问题的丈量办法应运而生。本文首要介绍了插接式智能组合电器中电子式光电组合互感器测验体系中的数据收集部分,剖析了其静态与动态特性,并提出了相应的差错补偿办法。
电子式互感器测验体系
电子式互感器测验体系首要由数据收集、数据传输以及数据处理与输出3部分组成。根本电路结构如图1所示。
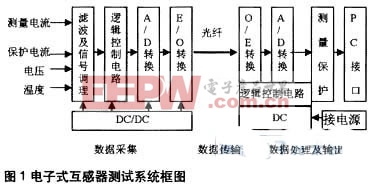
从图1能够看出,数据收集部分是整个测验体系的根底,对整个体系的准确度影响很大。因为收集体系收集的信号既有温度这样的缓变信号,又有电压、电流等周期信号,因而本文将对收集体系的静态及动态特性进行剖析,以寻求改进收集体系功能的办法。
静态特性剖析与差错补偿
静态特性指的是对收集体系加载静态信号后得到的功能指标,首要有线性度、直流增益、直流偏置、温度漂移等。
设x为体系输入,y为体系输出,k为体系的抱负增益(一般为1),则可得:y=kx。若在收集体系满量程规模内均匀地选取m个输入点,且在每个输入点上收集n个数据,则:
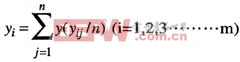
从而拟合出输入与输出间的最小二乘回归直线:y=kx+b
即可得到偏置差错Ep=b,增益差错Ek=k-k0,非线性差错Enl=max(yi-k·xi-b)。
为了进步丈量准确度,应采纳相应的差错补偿。现在遍及选用多项式拟合的办法,经过对丈量值y;的拟合,获取尽或许挨近理论值的成果。拟合联系为:

对电子式互感器而言,温度的影响不容忽视,偏置、增益差错以及非线性差错等都随温度改变而改变,用多项式拟合进行差错补偿时,有必要考虑温度作用,因而可得出: 式中:a0,a1,……,ah(t)为多项式的系数,是温度t的函数。因为此刻自变量有t和yt两个,所以不能按惯例系数确认办法来进行求解,这儿提出一种新的系数求解办法,在别离考虑t和yt的作用下进行求解。若在收集体系适用的温度规模内选取1个输入点,则可先假定温度tc(c=1,2,3……,1)不变,求取在该温度下的多项式系数。令:

对式中多项式系数别离求偏导,并令其为0,即可得到温度tc作用下的多项式系数。接下来就可别离求取1个不同温度下的多项式系数,然后再求解这些系数和温度间的拟合联系,求取办法与上述办法相同。
应当着重的是,差错补偿时多项式阶数应首要确认下来,也并不是阶数越高补偿作用就越好。高阶多项式在特定区间内的补偿作用能够是最佳的,但在该区间外则或许呈现极大的差错。所以,阶数的选取不只要考虑补偿的作用,还应当考虑补偿办法在拟合的进程也是先假定温度不变,求取一组多项式系数,然后再求取各组系数与温度间的多项式联系即可。多项式阶数的确认依然选用静态差错补偿中的办法。
数据收集体系的实测成果
依据前面说到的办法,对数据收集体系的静态特性与动态特性的实测成果进行了差错补偿,在补偿进程中,静态特性与动态特性的多项式阶数均取为4阶,而多项式系数与温度间的拟合多项式阶数在2~5阶之间灵敏设定。
结语
本文对数据收集体系的静态特性与动态特性进行剖析,提出了温度改变情况下收集体系的差错补偿办法。该补偿办法作用显着,有助于改进整个测验体系的温度稳定性。 需求阐明的是,本文从理论方面寻求最佳的补偿办法,而在完成进程中,假如有必要考虑使用计算机或DSP芯片进行处理,就不利于对丈量参量的实时处理。因而,应当依据实时性、准确性等归纳要求来选取最合适的补偿办法。
整个量程规模内的可拓展性。一般是先设定差错补偿的上限,满意这个差错上限的多项式阶数的最小值即为终究确认的多项式阶数。
动态特性的点评及差错补偿
动态特性反映的是收集体系加载动态信号后的功能。详细到电子式互感器,剖析动态特性时应先施加正弦波鼓励信号,然后经过傅立叶改换,获取输出信号的频谱特征,以此点评出收集体系的动态特性,从而提出相应的补偿办法。若收集体系容许信号的规模为±Ap,抱负增益为k0(一般为1),则施加正弦信号:e(t)=Apsin(2πft+α)。
式中,f为正弦信号的频率;α为正弦信号的初相角。发动收集体系,得到收集数据xi(i=1,2,3,……,n)。对收集数据进行傅立叶改换后,直流和基波重量为:a(t)=Asin(2πft+β)+d。
其间,A为基波信号的幅值;β为基波信号的初相角;d为直流重量。
这样,增益差错为Ek=A/Ap-k0,偏置差错为Ep=d,实践有效值差错为:
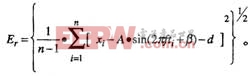
再由收集体系的抱负有效值差错Ei=0.289Ap/2b(b为模数转换器的位数),能够得到收集体系中模数转换器的动态有效位数:EB=b-log2(Er/Ei),从而定义出收集体系在频率f处对幅值为x的信号的收集准确度:
![]()
可见,收集体系的动态准确度将跟着频率、幅值的改变而改变。考虑到电子式互感器是对工频量进行丈量,因而暂不考虑频率改变的影响。不过,因为环境温度的改变对收集体系动态特性影响较大,进行差错补偿时,应当将环境温度改变带来的影响考虑进去。
动态特性的差错补偿仍旧采纳多项式拟合的办法,因为自变量有温度和幅值两个,所以采纳下面的多项式方式进行拟合:
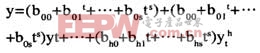
拟合的进程也是先假定温度不变,求取一组多项式系数,然后再求取各组系数与温度间的多项式联系即可。多项式阶数的确认依然选用静态差错补偿中的办法。
数据收集体系的实测成果
依据前面说到的办法,对数据收集体系的静态特性与动态特性的实测成果进行了差错补偿,在补偿进程中,静态特性与动态特性的多项式阶数均取为4阶,而多项式系数与温度间的拟合多项式阶数在2~5阶之间灵敏设定。
结语
本文对数据收集体系的静态特性与动态特性进行剖析,提出了温度改变情况下收集体系的差错补偿办法。该补偿办法作用显着,有助于改进整个测验体系的温度稳定性。 需求阐明的是,本文从理论方面寻求最佳的补偿办法,而在完成进程中,假如有必要考虑使用计算机或DSP芯片进行处理,就不利于对丈量参量的实时处理。因而,应当依据实时性、准确性等归纳要求来选取最合适的补偿办法。